POJ - 1905 Expanding Rods（二分+计算几何）

http://poj.org/problem?id=1905

题意

一根两端固定在两面墙上的杆，受热后变弯曲。求前后两个状态的杆的中点位置的距离

分析

很明显需要推推公式。

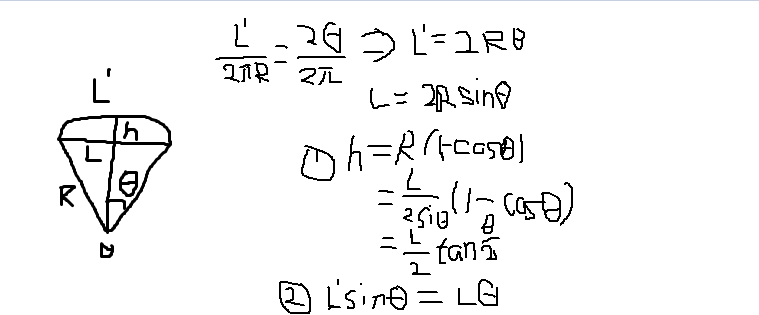
由②的限制条件来二分角度，答案由①给出。注意，这种写法的精度要求较高。

#include<iostream>
#include<cmath>
#include<cstring>
#include<queue>
#include<vector>
#include<cstdio>
#include<algorithm>
#include<map>
#include<set>
#define rep(i,e) for(int i=0;i<(e);i++)
#define rep1(i,e) for(int i=1;i<=(e);i++)
#define repx(i,x,e) for(int i=(x);i<=(e);i++)
#define X first
#define Y second
#define PB push_back
#define MP make_pair
#define mset(var,val) memset(var,val,sizeof(var))
#define scd(a) scanf("%d",&a)
#define scdd(a,b) scanf("%d%d",&a,&b)
#define scddd(a,b,c) scanf("%d%d%d",&a,&b,&c)
#define pd(a) printf("%d\n",a)
#define scl(a) scanf("%lld",&a)
#define scll(a,b) scanf("%lld%lld",&a,&b)
#define sclll(a,b,c) scanf("%lld%lld%lld",&a,&b,&c)
#define IOS ios::sync_with_stdio(false);cin.tie(0)
#define lc idx<<1
#define rc idx<<1|1
#define rson mid+1,r,rc
#define lson l,mid,lc
using namespace std;
typedef long long ll;
template <class T>
void test(T a){cout<<a<<endl;}
template <class T,class T2>
void test(T a,T2 b){cout<<a<<" "<<b<<endl;}
template <class T,class T2,class T3>
void test(T a,T2 b,T3 c){cout<<a<<" "<<b<<" "<<c<<endl;}
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3fll;
const ll mod = 1e9+;
int T;
void testcase(){
    printf("Case %d: ",++T);
}
const int MAXN = 1e5+;
const int MAXM = ;

int main() {
#ifdef LOCAL
    freopen("data.in","r",stdin);
#endif // LOCAL
    double l,n,c;
    while(~scanf("%lf%lf%lf",&l,&n,&c)){
        if(l<&&n<&&c<) break;
        double low=0.0,high=asin(1.0),mid;
        double L=(+n*c)*l;
        while(high-low>1e-){
            mid=(high+low)/;
            if(L*sin(mid)<=l*mid) high=mid;
            else low=mid;
        }
        printf("%.3f\n",l/*tan(low/));
    }
    return ;
}