Java实现偶数矩阵（Even Parity, UVa 11464）

偶数矩阵（Even Parity, UVa 11464）

问题描述

　　给你一个n×n的01矩阵（每个元素非0即1），你的任务是把尽量少的0变成1，

使得每个元素的上、下、左、右的元素（如果存在的话）之和均为偶数。

比如，如（a）所示的矩阵至少要把3个0变成1，最终如图（b）所示，才能保证其为偶数矩阵。

看图!

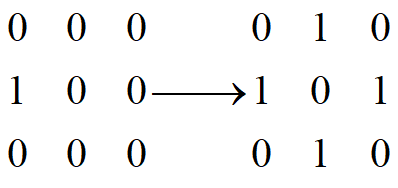
输入格式

　　输入的第一行为数据组数T（T≤30）。每组数据的第一行为正整数n（1≤n≤15）；

接下来的n行每行包含n个非0即1的整数，相邻整数间用一个空格隔开。

输出格式

　　对于每组数据，输出被改变的元素的最小个数。如果无解，应输出-1。

PS：

我虽然不能排列每一个，但我可以排类第一行，然后让后面的根据第一行进行排列

package 第七次模拟;

import java.util.Scanner;

public class Demo3矩阵 {
	static int n, Min,M=20;
	static int [] [] a  = new int [M][M];
	static int [] [] b  = new int [M][M];
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		  int cas, t = 0;
		    cas=sc.nextInt();
		    while(t++<cas)
		    {
		        n=sc.nextInt();
		        for(int i = 0; i < n; i++)
		            for(int j = 0; j < n; j++)
		               a[i][j]=sc.nextInt();

		        Min = Integer.MAX_VALUE;
		        dfs(0);//开始枚举；
		        System.out.printf("Case %d: ",t);
		        if(Min==1e9)
		        	 System.out.printf("-1\n");
		        else
		        	 System.out.printf("%d\n",Min);
		    }
	}
	static int check(int x, int y)//将其上左右三面的值相加
	{
	    int sum = 0;
	    if(x-1>=0) sum += b[x-1][y];
	    if(y-1>=0) sum += b[x][y-1];
	    if(y+1<n) sum += b[x][y+1];

	    return sum%2;//如果是偶数就返回0，奇数就返回1
	}
static	void dfs(int cur)
	{
	    //利用深度优先遍历枚举第一行
	    if(cur!=n)
	    {
	        b[0][cur] = 1;
	        dfs(cur+1);
	        b[0][cur] = 0;
	        dfs(cur+1);
	    }
	    else//枚举完之后开始递推下面每一行的情况
	    {
	        for(int i = 1; i < n; i++)
	            for(int j = 0; j < n; j++)
	                b[i][j] = check(i-1,j);
	        int cou = 0;
	        for(int i = 0; i < n; i++)
	            for(int j = 0; j < n; j++)
	                if(a[i][j]==1&&b[i][j]==0)
	                    return;//题目只能把0变1，不能把1变0，所以直接结束。
	                else if(a[i][j]==0&&b[i][j]==1)
	                    cou++;//只有当出现原来为0，枚举出的结果中为1的情况，cou才+1
	        if(Min>cou)
	            Min = cou;
	        return;
	    }

	}

}