TensorFlow2 Part1：基础

TensorFlow™是一个基于数据流编程（dataflow programming）的符号数学系统，被广泛应用于各类机器学习（machine learning）算法的编程实现，其前身是谷歌的神经网络算法库DistBelief [1] 。

它是现在最流行的机器学习框架，甚至在此领域大有要垄断的态势。

1. 直观理解
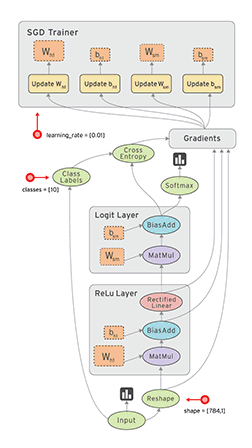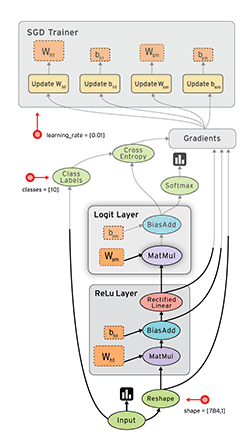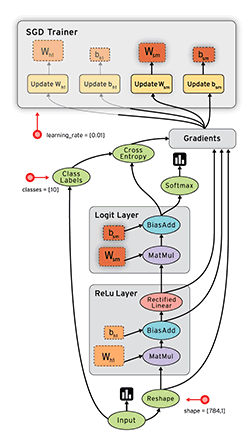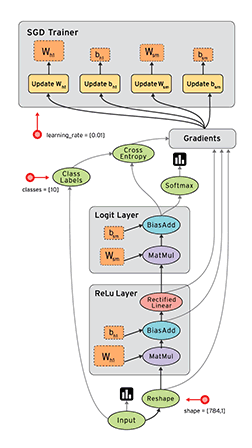
   • TensorFlow 把它拆成 tensor(张量即数据) 和 flow，就可很好的理解它为什么基于数据流进行编程
     
     

TensorFlow™ 是一个采用数据流图（data flow graphs），用于数值计算的开源软件库。节点（Nodes）在图中表示数学操作，图中的线（edges）则表示在节点间相互联系的多维数据数组，即张量（tensor）。它灵活的架构让你可以在多种平台上展开计算，例如台式计算机中的一个或多个CPU（或GPU），服务器，移动设备等等。TensorFlow 最初由Google大脑小组（隶属于Google机器智能研究机构）的研究员和工程师们开发出来，用于机器学习和深度神经网络方面的研究，但这个系统的通用性使其也可广泛用于其他计算领域。

数据流图用“结点”（nodes）和“线”(edges)的有向图来描述数学计算。“节点” 一般用来表示施加的数学操作，但也可以表示数据输入（feed in）的起点/输出（push out）的终点，或者是读取/写入持久变量（persistent variable）的终点。“线”表示“节点”之间的输入/输出关系。这些数据“线”可以输运“size可动态调整”的多维数据数组，即“张量”（tensor）。张量从图中流过的直观图像是这个工具取名为“Tensorflow”的原因。一旦输入端的所有张量准备好，节点将被分配到各种计算设备完成异步并行地执行运算。

1. TensorFlow 安装

• 这个安装是最拿人的了，GPU版本的性能要比CPU版本的好上很多，但是因为要配置显卡，所以更加难安装，（另外笔者的电脑GPU是GTX-1050TI装不了GPU版本），而入门的话CPU就够了，此处只简单的记录一下如何安装CPU版本。

  • 配置：
    
    Win10 ； python3.6 ；tensorflow 1.14.0

  • 说明：

    • 对于CPU版本，不需要安装anaconda也能行的
    • 因为安装的时候会有额外的安装许多的包，所以最好创建一个虚拟环境，在虚拟环境中安装TensorFlow。

  • 步骤：

    • 直接用pip的话，比较慢，所以建议在pypi网站中下载好whl文件，再进行安装，注意，此时一定要对应好版本，否则会出现很多问题。
    • 把下载好的whl文件移动到虚拟环境文件夹中，再使用pip进行安装，此时同时会自动安装必要的包。此时建议科学上网，否则安装的会比较慢。
    • 安装完成后，在虚拟环境中import tensorflow成功那就大功告成了。
    • 如果此时出现了一些问题，看提示出现Numpy的字眼的话，那么很有可能是因为Numpy 的版本太高了，安装1.16版本就好了

1. 使用anaconda进行安装

• 再次试了用anaconda进行安装，换用了清华大学的源，真的快了不是一点半点

• 安装anaconda：
  
  按步骤安装就行，只注意要勾选加入路径，和默认用anaconda的python解释器，安装完成后在pycharm中解释器的路径在anaconda文件中的Script文件中找python.exe，pycharm也就能用了。

• 换装清华的源

conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/
conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/main/
conda config --set show_channel_urls yes
之后安装就可以用conda了，conda的操作和pip几乎一摸一样
pip list  /  conda list
pip install 【package】== version / conda install 【package】= version
pip install 【package】 --upgrade / conda update 【package】 

• 安装虚拟环境

我们在安装conda的时候默认创建了一个base环境，使用的是anaconda的默认解释器（我的是3.7），但为了防止包混乱，我们可以为tensorflow创建一个独立的环境。

conda create --name tf python=3.7		/创建一个名为tf的虚拟环境，里面安装的解释器为python3.7版本
C:\Users\12521>conda env list			/此时在看看包含的env中除了base还有个tf
# conda environments:
#
base                  *  C:\Users\12521\Anaconda3
tf                       C:\Users\12521\Anaconda3\envs\tf
C:\Users\12521>activate tf				/激活tf
(tf) C:\Users\12521>						/成功

• conda虚拟环境的操作：

	-	conda create --name [env-name]      # 建立名为[env-name]的Conda虚拟环境
	-	conda activate [env-name]           # 进入名为[env-name]的Conda虚拟环境
	-	conda deactivate                    # 退出当前的Conda虚拟环境
	-	conda env remove --name [env-name]   # 删除名为[env-name]的Conda虚拟环境
	-	conda env list                      # 列出所有Conda虚拟环境

• 并不是所有的英伟达显卡都支持GPU版本，此时此刻，对于笔记本来说GTX系列所有带Ti的高配版本都用不了！mmp。
• 不过cpu版本就够玩了，真正的大项目不可能用笔记本，都要用工作站的。
• 清华的镜像站tensorflow版本比较低，笔者要安装最新的2.0Beta版本的尝鲜

 pip install tensorflow==2.0.0-beta0
/ 安装完成后import还是不能用
 pip install numpy == 1.16
 /numpy版本太高，安装低一点的就好了

1. Tensorflow的亮点

• tensorflow的许多语法和python numpy十分的类似。PS:说实话不如matlab和octave简洁。。
• 机器学习模型并不是只能够使用tensorflow，类似matlab，octave，python numpy 等都可以编写机器学习模型。
• tensorflow与之相比主要有两处亮点：
  • 自动求偏导数。比如当非常复杂的神经网络进行反向传播的时候，如果手工求偏导那么无疑非常麻烦，甚至不可行。自动求偏导这个功能就显得大大的有用。
  • 自动更新参数。原因与上述类似。

1. Tensorflow基础

• tensor是张量的意思，它是指多维数组，同时还有0维数组（标量），1维（向量），2维（矩阵）
• 快速生成张量：
  • 生成随机标量：

>>> random_float = tf.random.uniform(shape=())
>>> print(random_float)
tf.Tensor(0.9904655, shape=(), dtype=float32)
>>>random_float = tf.random.uniform(shape=(2,3))
>>> print(random_float)
tf.Tensor(
[[0.7376052  0.25581563 0.1726948 ]
 [0.74306595 0.18850088 0.2021966 ]], shape=(2, 3), dtype=float32)

• 生成向量

//一般生成方式
>>> vector = tf.constant([[1,2],[3,4]])
>>> print(vector)
tf.Tensor(
[[1 2]
 [3 4]], shape=(2, 2), dtype=int32)
//zeros
>>> zero_vector = tf.zeros(shape=(2))
>>> print(zero_vector)
tf.Tensor([0. 0.], shape=(2,), dtype=float32)
>>> zero_vector = tf.zeros(shape=(2,3))
>>> print(zero_vector)
tf.Tensor(
[[0. 0. 0.]
 [0. 0. 0.]], shape=(2, 3), dtype=float32)
 //ones
>>> one_vector = tf.ones(shape=(2))
>>> print(one_vector)
tf.Tensor([1. 1.], shape=(2,), dtype=float32)
>>> one_vector = tf.ones(shape=(2,2))
>>> print(one_vector)
tf.Tensor(
[[1. 1.]
 [1. 1.]], shape=(2, 2), dtype=float32)
//eye生成单位向量，此处就没有shape=（）了了了
>>> eye_vector = tf.eye(3)
>>> eye_vector
<tf.Tensor: id=64, shape=(3, 3), dtype=float32, numpy=
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]], dtype=float32)>

• 生成张量（与生成向量完全类似）

>>> zero_vector = tf.zeros(shape=(2,3,4))
>>> print(zero_vector)
tf.Tensor(
[[[0. 0. 0. 0.]
  [0. 0. 0. 0.]
  [0. 0. 0. 0.]]
 [[0. 0. 0. 0.]
  [0. 0. 0. 0.]
  [0. 0. 0. 0.]]], shape=(2, 3, 4), dtype=float32)
>>> one_vector = tf.ones(shape=(2,3,4))
>>> print(one_vector)
tf.Tensor(
[[[1. 1. 1. 1.]
  [1. 1. 1. 1.]
  [1. 1. 1. 1.]]
 [[1. 1. 1. 1.]
  [1. 1. 1. 1.]
  [1. 1. 1. 1.]]], shape=(2, 3, 4), dtype=float32)
  ········

• 张量的重要属性

//上代码
>>> vector = tf.constant([[1,2],[3,4]])
//形状
>>> vector.shape()
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: 'TensorShape' object is not callable
>>> vector.shape
TensorShape([2, 2])
//数据类型
>>> vector.dtype
tf.int32
>>> vector = tf.constant([[1,2],[3,4]],dtype=tf.float32)	//在定义张量的时候可以
>>> print(vector)
tf.Tensor(
[[1. 2.]
 [3. 4.]], shape=(2, 2), dtype=float32)
//以numpy方法获得
>>> A = vector.numpy
>>> print(A)
<bound method _EagerTensorBase.numpy of <tf.Tensor: id=66, shape=(2, 2), dtype=int32, numpy=
array([[1, 2],
       [3, 4]])>>
>>> print(vector)
tf.Tensor(
[[1 2]
 [3 4]], shape=(2, 2), dtype=int32)
>>> type(A)
<class 'method'>
>>> type(vector)
<class 'tensorflow.python.framework.ops.EagerTensor'>
/张量的 numpy() 方法是将张量的值转换为一个NumPy数组。

• 矩阵的加法
  
  必须得是shape和dtype都相同的才能够做加法

>>> B = tf.ones(shape=(2,3))				//默认生成的数据类型一般是float32
>>> C = tf.ones(shape=(2,3))
>>> tf.add(B,C)									//shape相同，相加成功
<tf.Tensor: id=93, shape=(2, 3), dtype=float32, numpy=
array([[2., 2., 2.],
       [2., 2., 2.]], dtype=float32)>
>>> B = tf.ones(shape=(2,2))
>>> tf.add(B,C)									//改变B的shape，add失败
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "C:\Users\12521\Anaconda3\envs\tf\lib\site-packages\tensorflow\python\ops\gen_math_ops.py", line 392, in add
    _six.raise_from(_core._status_to_exception(e.code, message), None)
  File "<string>", line 3, in raise_from
tensorflow.python.framework.errors_impl.InvalidArgumentError: Incompatible shapes: [2,2] vs. [2,3] [Op:Add]
 >>> A = tf.constant([[1,2],[3,4]])
>>> A
<tf.Tensor: id=73, shape=(2, 2), dtype=int32, numpy=
array([[1, 2],
       [3, 4]])>
>>> B
<tf.Tensor: id=97, shape=(2, 2), dtype=float32, numpy=
array([[1., 1.],
       [1., 1.]], dtype=float32)>
>>> tf.add(A,B)								//A与B的shape相同，但是dtype不同，所以就失败聊
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "C:\Users\12521\Anaconda3\envs\tf\lib\site-packages\tensorflow\python\ops\gen_math_ops.py", line 392, in add
    _six.raise_from(_core._status_to_exception(e.code, message), None)
  File "<string>", line 3, in raise_from
tensorflow.python.framework.errors_impl.InvalidArgumentError: cannot compute Add as input #1(zero-based) was expected to be a int32 tensor but is a float tensor [Op:Add]

• 矩阵的乘法
  • emmmm~大一还没学线代，有点尴尬，缺啥补啥吧

//先来个简单的
>>> A = tf.constant([[1,2],[3,4]])
>>> B = tf.constant([[5,6,7],[8,9,10]])
>>> A						//创建一个2*2的向量A
<tf.Tensor: id=100, shape=(2, 2), dtype=int32, numpy=
array([[1, 2],
       [3, 4]])>
>>> B						//创建一个2*3的向量B
<tf.Tensor: id=101, shape=(2, 3), dtype=int32, numpy=
array([[ 5,  6,  7],
       [ 8,  9, 10]])>
>>> tf.matmul(A,B)			//进行矩阵A与B之间的乘法运算
<tf.Tensor: id=104, shape=(2, 3), dtype=int32, numpy=
array([[21, 24, 27],
       [47, 54, 61]])>
//从此例子入手，矩阵的乘法法则必须满足【矩阵A的列数必须与矩阵B的行数相同】。
//生成的的矩阵C的shape是   【A的row】*【B的column】
//具体进行的乘法运算是【A的第x行】*【B的第y列】得到矩阵C的（x,y）位置的元素
//emmm~至少目测是这样子的，有错误以后学了就知道了
//numpy存在广播机制，不知道tensorflow有没有
//上代码
>>> A
<tf.Tensor: id=109, shape=(2, 1), dtype=int32, numpy=
array([[1],
       [3]])>
>>> B
<tf.Tensor: id=108, shape=(2, 3), dtype=int32, numpy=
array([[ 5,  6,  7],
       [ 8,  9, 10]])>
>>> C
<tf.Tensor: id=114, shape=(2, 2), dtype=int32, numpy=
array([[1, 1],
       [1, 3]])>
>>> tf.add(A,B)
<tf.Tensor: id=118, shape=(2, 3), dtype=int32, numpy=
array([[ 6,  7,  8],
       [11, 12, 13]])>
>>> tf.add(A,C)
<tf.Tensor: id=120, shape=(2, 2), dtype=int32, numpy=
array([[2, 2],
       [4, 6]])>
>>> tf.add(B,C)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "C:\Users\12521\Anaconda3\envs\tf\lib\site-packages\tensorflow\python\ops\gen_math_ops.py", line 392, in add
    _six.raise_from(_core._status_to_exception(e.code, message), None)
  File "<string>", line 3, in raise_from
tensorflow.python.framework.errors_impl.InvalidArgumentError: Incompatible shapes: [2,3] vs. [2,2] [Op‘
//事实证明，tensorflow同样存在广播机制
PS：顺便把之前弄的稀里糊涂的广播机制也搞明白了，嘿嘿嘿
//上代码用向量A和C验证
>>> A
<tf.Tensor: id=109, shape=(2, 1), dtype=int32, numpy=
array([[1],
       [3]])>
>>> C
<tf.Tensor: id=114, shape=(2, 2), dtype=int32, numpy=
array([[1, 1],
       [1, 3]])>
>>> D								//向量D是对照着C用1将向量A补全到与C的shape相同（用1补前面）
<tf.Tensor: id=122, shape=(2, 2), dtype=int32, numpy=
array([[1, 1],
       [1, 3]])>
>>> tf.add(A,C)
<tf.Tensor: id=126, shape=(2, 2), dtype=int32, numpy=
array([[2, 2],
       [4, 6]])>
>>> tf.add(D,C)						//经过验证成立
<tf.Tensor: id=128, shape=(2, 2), dtype=int32, numpy=
array([[2, 2],
       [2, 6]])>

• tensorflow的自动求导机制

  • 此处以y=x^2为例

    • 初始化变量.
      
      变量与普通张量的一个重要区别是其默认能够被TensorFlow的自动求导机制所求导，因此往往被用于定义机器学习模型的参数。

>>> x1 = tf.Variable(tf.random.uniform(shape=()))				//生成随机数标量下x1
>>> x1
<tf.Variable 'Variable:0' shape=() dtype=float32, numpy=0.009866357>
>>> x2 = tf.Variable(3)											//生成标量x2==3
>>> x2
<tf.Variable 'Variable:0' shape=() dtype=int32, numpy=3>
>>> x3 = tf.Variable(3,name='bianliang3')						//生成标量x3==3,并且命名为bianliang3
>>> x3
<tf.Variable 'bianliang3:0' shape=() dtype=int32, numpy=3>
>>> x4 = tf.Variable(tf.constant([[1,2],[3,4]]))				//生成向量x4
>>> x4
<tf.Variable 'Variable:0' shape=(2, 2) dtype=int32, numpy=
array([[1, 2],
       [3, 4]])>

• • 自动求导模板

with tf.GradientTape() as tape:
		tape.watch([w])
		y = f（[w])​	
y_grad = tape.gradient(y, [w])

//先来个简单的标量求导
//实例代码：
>>> x2 = tf.Variable(3)
>>> with tf.GradientTape() as tape:
...     tape.watch(x2)
...     y = tf.square(x2)
...
WARNING: Logging before flag parsing goes to stderr.
W0815 07:57:30.611359 10928 backprop.py:842] The dtype of the watched tensor must be
floating (e.g. tf.float32), got tf.int32					//不能用int32？
>>> x = tf.Variable(3.)										//试试float32
>>> x
<tf.Variable 'Variable:0' shape=() dtype=float32, numpy=3.0>
>>> with tf.GradientTape() as tape:
...     tape.watch(x)
...     y = tf.square(x)
...
>>> y_grad = tape.gradient(y,x)								//it does work！
>>> print(y,y_grad)
tf.Tensor(9.0, shape=(), dtype=float32) tf.Tensor(6.0, shape=(), dtype=float32)

//事实上在机器学习中，只有很少且在很简单的问题上才会对标量进行求导，求导更多的应用场景
是【向量->标量】【向量->向量】
//实例问题，求简单线性回归函数的 Cost Function
//问题解析：
多变量线性回归问题模型 ： y = (w1)*(x1) +(w2)*(x2)+...+b
Cost Function：0.5 * Sigma[1~n] {y - y(实际值)}^2
偏导值：d【Cost Function{w，b}】/d【w】					//即Cost Function对变量的偏导数
//上代码
>>> x = tf.constant([[1.,2.],[3.,4.]])
>>> y = tf.constant([[1],[2]])
>>> w = tf.Variable([[1.],[2.]])
>>> w													//w是变量，需要用tf.Varible初始化
<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[1.],
       [2.]], dtype=float32)>
>>> b=1								//b是Bias，一般是1，不会变，设为常量应该没毛病，应该吧。。
>>> with tf.GradientTape() as tape:
...     CF = 1/2*tf.reduce_sum(tf.square(tf.matmul(x,w)+b-y))
...
Traceback (most recent call last):
  File "<stdin>", line 2, in <module>
  File "C:\Users\12521\Anaconda3\envs\tf\lib\site-packages\tensorflow\python\ops\math_op
  s.py", line 884, in binary_op_wrapper
    return func(x, y, name=name)
  File "C:\Users\12521\Anaconda3\envs\tf\lib\site-packages\tensorflow\python\ops\gen_mat
  h_ops.py", line 11571, in sub
    _six.raise_from(_core._status_to_exception(e.code, message), None)
  File "<string>", line 3, in raise_from
tensorflow.python.framework.errors_impl.InvalidArgumentError: cannot compute Sub as inp
ut #1(zero-based) was expected to be a float tensor but is a int32 tensor [Op:Sub] name
: sub/									//日常翻车。。不慌。看来又是dtype弄差了。
>>> y = tf.constant([[1.],[2.]])
>>> with tf.GradientTape() as tape:				//果然，重置y的dtype==float32就欧了
...     CF = 1/2*tf.reduce_sum(tf.square(tf.matmul(x,w)+b-y))
...
>>> w_grad = tape.gradient(CF,w)
>>> print(CF,w_grad)
tf.Tensor(62.5, shape=(), dtype=float32) tf.Tensor(
[[35.]
 [50.]], shape=(2, 1), dtype=float32)
>>> print(CF.numpy(),w_grad.numpy())			//用numpy的形式更加直观打印出结果
62.5 [[35.]
 [50.]]
 //分析结果很容易的得出结论，对应于w=[1,2]^T(转置)，b=1的情况下， Cost Function==62.5，
 d【Cost Function{w，b}】/d【w】== [35.，50.]^T

//对于b还是不是很放心。
>>> y = tf.constant([[1.],[2.]])
>>> x = tf.constant([[1.,2.],[3.,4.]])
>>> w = tf.Variable([[1.],[2.]])
>>> b = 1
>>> with tf.GradientTape() as tape:
...     CF = 1/2*tf.reduce_sum(tf.square(tf.matmul(x,w)+b-y))
...
>>> b_grad = tape.gradient(CF,b)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "C:\Users\12521\Anaconda3\envs\tf\lib\site-packages\tensorflow\python\eager\backp
  rop.py", line 986, in gradient
    if not t.dtype.is_floating:
AttributeError: 'int' object has no attribute 'dtype'
				//又翻车了。。问题出在b是个普通的常量，初始化成变量才能求导
>>> b = tf.Variable(1.)
>>> with tf.GradientTape() as tape:
...     CF = 1/2*tf.reduce_sum(tf.square(tf.matmul(x,w)+b-y))
...
>>> b_grad = tape.gradient(CF,b)
>>> print(b_grad)
tf.Tensor(15.0, shape=(), dtype=float32)	//emmm~为什么等于15？偶谢特马惹发克，看不懂呐。。

1. TensorFlow简单实例问题 – 线性回归问题之房价预测

• 解题步骤回顾

1. 引入数据
2. 对数据进行处理，特征缩放
3. 初始化参数【w】【b】
4. 设置迭代次数
5. 设置学习率（SGD函数）
6. 设置梯度下降迭代器
7. 使用梯度下降记录器
8. 记录器内部记录：定义模型；Cost Function
9. 利用tape.gradient自动计算损失函数关于模型参数的梯度
10.根据梯度自动更新参数
11. 具体参见 机器学习phase1

• TensorFlow下的线性回归

//numpy处理数据有一套（而且比tensorflow代码简单，少打俩字），引入进行预处理
>>> import numpy as np
>>> x_row = np.array([2013,2014,2015,2016,2017],dtype=np.float32)
>>> y_row = np.array([12000,14000,15000,16500,17500],dtype=np.float32)
>>>
>>> X = (x_row - x_row.min())/(x_row.max()-x_row.min())
>>> Y = (y_row - y_row.min())/(y_row.max()-y_row.min())			//此处的处理第一眼看有点懵
>>> x_row - x_row.min()
array([0., 1., 2., 3., 4.], dtype=float32)
>>> X
array([0.  , 0.25, 0.5 , 0.75, 1.  ], dtype=float32)
>>> Y
array([0.        , 0.36363637, 0.54545456, 0.8181818 , 1.        ],
      dtype=float32)
//到这儿就看懂了，这就是特征缩放呐，这样做有利于梯度下降
//分析上述操作，x_row - x_row.min()所作的是将x_row向量每一项都减去该向量中的最小值，即
x_row.min()，这一步操作产生的结果就是 新的向量x_row都缩小了，并且必定有一项是0（即原来那个
x_row.min()项）。再看分母是 x_row.max()-x_row.min() >= 0 , 在上下相除之后，必定有一项是0，
还有一项是1（即原来那个x_row.max()，该项的分子分母相等），其余的项都是在0~1之间，所以说，这
一顿骚操作，成功的把向量x_row 中每一项的值都限定在了0~1之间，这样梯度下的就快多了

//上tensorflow
>>> import tensorflow as tf
>>> x = tf.constant(X)			//引入数据
>>> y = tf.constant(Y)
>>> w = tf.Variable(0.)	//初始化参数为0.就行了（注意dtype一定得是float32呐，不然报错又得敲一遍。。）
>>> b = tf.Variable(0.)
>>> variables = [w,b]			//变量组
>>> num_epoch = 10000			//梯度下降的次数就设为10000了
>>> optimizer = tf.keras.optimizers.SGD(learning_rate=1e-3)	//声明一个Gradient Descent Optimizer（梯度下降优化器）
>>> optimizer = tf.keras.optimizers.SGD(1e-3)				//能省点代码就省一点啊
//在optimizer(优化器)中设定学习率为1e-3，是个负数，大概是-0.28，可以实现缓缓的下降，讲究~
>>> for e in range(num_epoch):
...     with tf.GradientTape() as tape:
...             y_pred = w*x+b
...             CF = 0.5 * tf.reduce_sum(tf.square(y_pred - y))
...     grads = tape.gradient(CF,variables)
...     optimizer.apply_gradients(grads_and_vars=zip(grads,variables))
...
WARNING: Logging before flag parsing goes to stderr.
W0815 22:40:00.175946 18276 backprop.py:990] The dtype of the source tensor must be floating (e.g. tf.float32) when calling GradientTape.gradient, got tf.int32
W0815 22:40:00.180869 18276 backprop.py:990] The dtype of the source tensor must be floating (e.g. tf.float32) when calling GradientTape.gradient, got tf.int32
Traceback (most recent call last):
  File "<stdin>", line 6, in <module>
  File "C:\Users\12521\Anaconda3\envs\tf\lib\site-packages\tensorflow\python\keras\optimizer_v2\optimizer_v2.py", line 427, in apply_gradients
    grads_and_vars = _filter_grads(grads_and_vars)
  File "C:\Users\12521\Anaconda3\envs\tf\lib\site-packages\tensorflow\python\keras\optimizer_v2\optimizer_v2.py", line 975, in _filter_grads
    ([v.name for _, v in grads_and_vars],))
ValueError: No gradients provided for any variable: ['Variable:0', 'Variable:0'].
//欧谢他妈惹法克，又翻车。。

//再敲一边居然就成了？！

>>> for e in range(num_epoch):				//设置for循环
...     with tf.GradientTape() as tape:		//梯度下降记录器
...             y_pred = w*x+b						//模型
...             CF = 0.5 * tf.reduce_sum(tf.square(y_pred - y))  //Cost Function
...     grads = tape.gradient(CF,variables)						 //求偏导
...     optimizer.apply_gradients(grads_and_vars=zip(grads,variables))
...
//此处省略9998行梯度下降记录~
<tf.Variable 'UnreadVariable' shape=() dtype=int64, numpy=9999>
<tf.Variable 'UnreadVariable' shape=() dtype=int64, numpy=10000>

//代码的进一步说明：
//调用优化器的apply_gradients()方法，传入Cost function 和 参数，优化器能帮我们在进行完一次梯度
下降之后按照我们之前设定的 learning_rate(在这里我们设定的值是1e-3)自动更新参数.
//函数需要提供的参数 grads_and_vars 包括两部分，一是要求的偏导数（此处即grads，Cost Function对
变量的偏导数）；另一个就是要更新的变量（此处即variables）。

//两者需要一个 zip（）函数打包一下，具体效果试试看
//效果代码：
>>> grads
[<tf.Tensor: id=440038, shape=(), dtype=float32, numpy=-0.002667658>,
<tf.Tensor: id=440031, shape=(), dtype=float32, numpy=0.0014782436>]
>>> grads.numpy()
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
AttributeError: 'list' object has no attribute 'numpy'	  //是个列表？
>>> type(grads)
<class 'list'>
>>> type(variables)
<class 'list'>					//都是个列表
>>> yo = zip(grads,variables)
>>> type(yo)
<class 'zip'>					//打包之后的类型是 zip object
>>> print(yo)
<zip object at 0x0000016118513A88>
>>> list(yo)					//用列表的形式能够展示出来
[(<tf.Tensor: id=440038, shape=(), dtype=float32, numpy=-0.002667658>, <tf.Variable 'Variable:0' shape=() dtype=float32, numpy=0.97637>), (<tf.Tensor: id=440031, shape=(), dtype=float32, numpy=0.0014782436>, <tf.Variable 'Variable:0' shape=() dtype=float32, numpy=0.057565063>)]

• zip函数效果如图所示：
  
  

//梯度下降最后结果：
>>> print(w,b)
<tf.Variable 'Variable:0' shape=() dtype=float32, numpy=0.97637>
<tf.Variable 'Variable:0' shape=() dtype=float32, numpy=0.057565063>
>>> print(w.numpy(),b.numpy())				//结果用numpy格式展示，梯度下降成功！
0.97637 0.057565063
											//

欲戴桂冠，必承其重. --酒后听得真言

心满意足的一天。19.8.16