计量经济与时间序列_自协方差(AutoCovariance)算法解析(Python)

1　　样本的自协方差函数的通式如下：

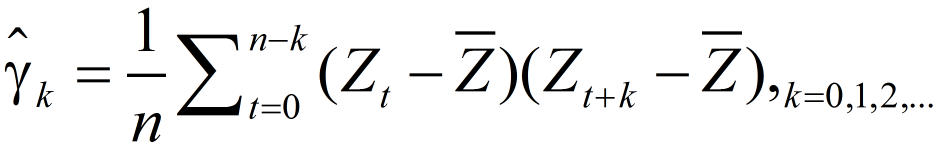
2　　其实，后面要计算的自相关函数也可以用自协方差来表示：

 # @author: "Thomas.Shih"
 # @date: 2018/3/5 0005
 # !/usr/bin/python3
 # -*- coding:utf-8 -*-
 TimeSeries = [11.67602657, 5.637492979, 1.375516942, 0.618705492, -0.152047234, -0.508555434, -6.065288121, -9.417602801, \
               -10.47205437, -8.018063902, 0.523277554, 4.86893283, 4.23977562, -10.2344375, -3.463362573, 36.51326577, \
               -8.518370963, -15.37474905, -7.687911176, 4.818978874, 7.876681639, 1.763788865]
 Zt = []
 LZt = []
 AutoCovariance = []
 # 自协方差存为列表形式，显示格式如下：
 # [γ0,γ1,γ2,γ3,....]
 # [γk,....]  k = 0,1,2,3....
 total = 0
 i = 1
 while i < len(TimeSeries):
     L = TimeSeries[i::]
     LL = TimeSeries[:-i:]
     total = total + TimeSeries[i - 1]
     Zt.append(L)
     LZt.append(LL)
     i += 1
 total = total + TimeSeries[-1]
 avg = total / len(TimeSeries)

 k = 0
 result_temp0 = 0
 # 首先求γ0的值
 while k < len(TimeSeries):
     result_temp0 = result_temp0 + pow((TimeSeries[k] - avg), 2)
     k += 1
 AutoCovariance.append(result_temp0/len(TimeSeries))
 # print(AutoCovariance)
 # 显示结果：
 #[2418.4380925669107]

 # 然后计算分子
 p = 0
 q = 0
 length = 0
 while p < len(Zt):
     q = 0
     result_temp1 = 0
     while q < len(Zt[p]):
         result_temp1 = result_temp1 + (Zt[p][q] - avg) * (LZt[p][q] - avg)
         q += 1
     # print(result_temp1)
     # print(len(Zt)-p)
     AutoCovariance.append(result_temp1/len(TimeSeries))
     p += 1
 print(AutoCovariance)
 # print(len(AutoCovariance))
 # print(len(Zt))

 # 显示结果：
 # [109.92900420758684, 7.033249208759847, -41.331023616868386, -9.818640497993421, 17.321104958520728, 11.540453909308482,
 # -20.71675731505552, -23.35193308926872, -10.671711257152637, 2.3511837591142006, 12.09337228027552, 5.284907080510467,
 # -3.4833058404578527, -9.53177380894126, 3.568570997073478, 15.31665885468035, -8.901077316598432, -9.619216801963882,
 # -2.303250941136475, 4.686244739096256, 4.632349610445184, 0.9360929838586473]