51nod A 魔法部落(逆元费马小定理)

A 魔法部落

小Biu所在的部落是一个魔法部落，部落中一共有n+1个人，小Biu是魔法部落中最菜的，所以他的魔力值为1，魔法部落中n个人的魔法值都不相同，第一个人的魔法值是小Biu的3倍，第二个人的魔法值是第一个人的3倍，以此类推。

现在小Biu想知道整个部落的魔法值和是多少？由于答案比较大，请把答案对1e9+7取模之后输出。

收起

 

输入

输入一个数N(0 <= N <= 10^9)

输出

输出：整个部落的魔法值和模1e9+7。

数据范围

对于20%的数据，n<=100；
对于40%的数据，n<=1000000；
对于100%的数据，n<=1000000000；

输入样例

3

输出样例

40

样例解释

3^0+3^1+3^2+3^3 = 1+3+9+27 = 40

　　题意如此，此为等比数列，根据等比求和公式，为（3^(n+1)-1）/2　　mod1e9+7

　　由于n很大，做除数再取模会损失精度，所以我们需要把他转化为乘法来计算。那么就用到了逆元思想。

　　逆元：方程  的解称为  关于模  的逆，意思也为:ax%p==1。当 （即 ， 互质）时，方程有唯一解，否则无解。

　　　　　　x为a关于p的逆元。

　　　　我们把式子写成(a/b)%m,推理过程如下,字迹潦草，勿怪

　　即我们需要求(a*c)mod  m。c为b的逆元。

　　费马小定理：当  为质数时，有 ，那么易得出 。

　　根据题意，mod=1e9+7，即为p的位置，mod为质数，适用于费马小定理求逆元，c的位置即为b^(p-2)的位置，这样根据b求c就可以了。。b=2，则求2^(mod-2),利用快速幂来求

　　

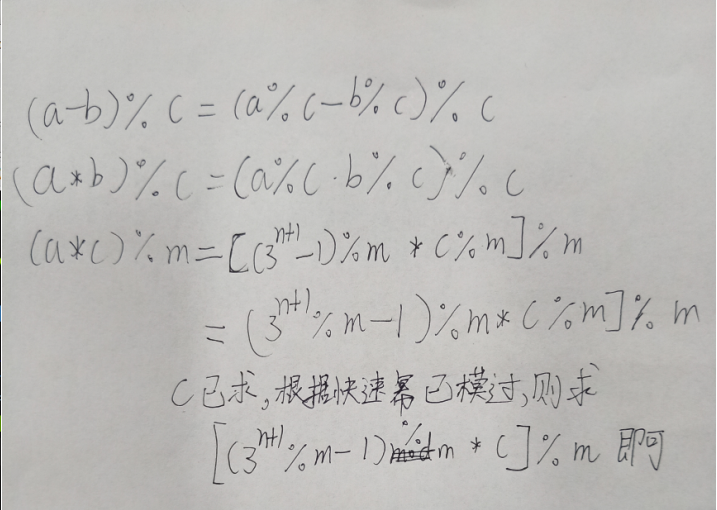
　　上代码：

#include<iostream>
using namespace std;
typedef long long ll;
const int mod=1e9+;
int qk(ll a, ll b)
{
    ll ans=;
    a=a%mod;
    while(b)
    {
        if(b%==)
            ans=(ans*a)%mod;
        b=b/;
        a=(a*a)%mod;
    }
    return  ans;
}
int main(){
    ll n;
    while(cin>>n)
    {
        ll c=qk(,mod-);
        ll zi=qk(,n+)-;
        cout<<(zi%mod*c)%mod<<endl;
    }
}

一个队友给的优化，直接快速幂 ，模的时候mod*2即可，排除了结果为5e8的情况，那样会出现精度丢失...