使用python求解向量值函数的雅各比(Jacobian)矩阵

　　考虑一个向量值函数$R^m \rightarrow R^n$，即$\textbf{y} = f(\textbf{x})$，它的雅各比(Jacobian)矩阵定义如下。

　　

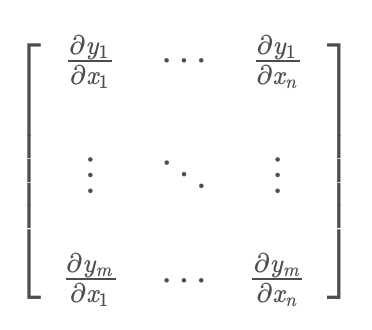
　　下面记录下一段使用python求向量值函数Jacobian矩阵的代码，只有向量值函数可用，如果为标量函数则会报错。

import torch

# 定义函数
x = torch.tensor([1, 3, 5.], requires_grad=True)
A = torch.tensor([[1., 0, 1], [0, 1, 0], [1, 0, 1]])
y = A@x

Weight = torch.eye(y.size()[0])
B = torch.tensor([])
for i, weight in enumerate(Weight):
    B = torch.cat((B, torch.autograd.grad(y, x, grad_outputs=weight, retain_graph=True)[0]), 0)
print(B.view((y.size()[0], -1)))

　　这里我们以$x=[1,3,5]^T, y=Ax$为例，输出结果如下: