[算法] Dijkstra算法（带权有向图 最短路径算法）

一、带权有向图

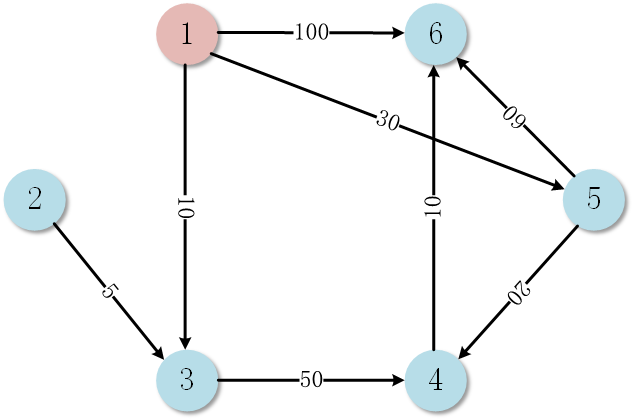
二、算法原理

1）由于我们的节点是从1-6，所以我们创建的列表或数组都是n+1的长度，index=0的部分不使用，循环范围为1-6（方便计算）。

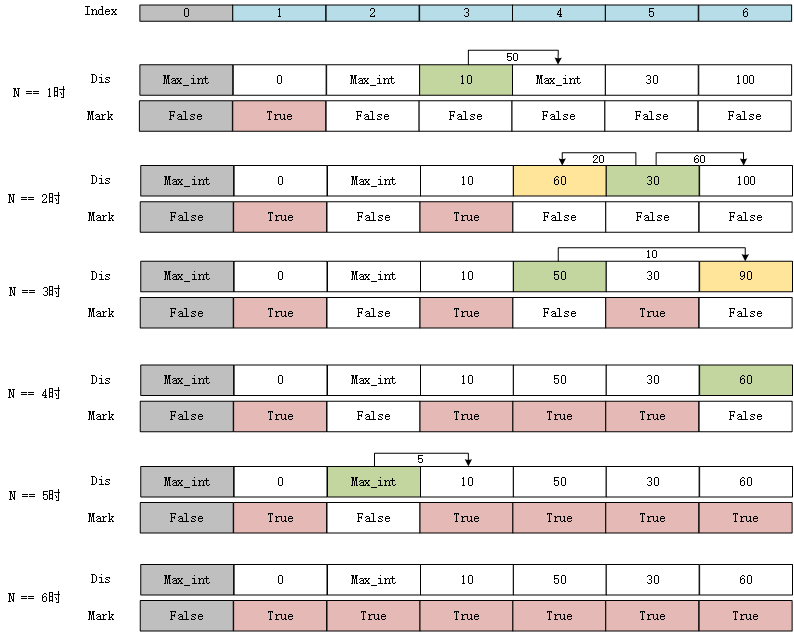
2）循环之前，我们先初始化dis数组和mark数组：

　　dis数组中保存我们需要求的开始点（start），到其余所有点的最短路径。初始化的时候，只初始化到自己能够直接到的节点的距离，不能直接到的距离初始化为max_int（即sys.maxsize）。

　　mark保存节点的状态，如果已经被计算过，则状态为True，还未被计算过，则为False

3）开始循环，注意，我们只循环[1,n]的范围。index==0不纳入循环。

4）N==1时，找到所有Dis元素中，对应mark元素为False的元素。找出其中最小值为10，对应的index为3，也就是节点3。然后在weight数组中，找到3能直接到的节点（且对应mark也要为False），这里找到3能直接到4号节点，且权重为50。此时判断dis[3]+50<dis[4]，如果成立，则使用dis[3]+50更新dis[4]。由于dis[4]等于max_int，所以dis[4]被更新为60。

5）N==2时，找到所有Dis元素中，对应mark元素为False的元素。找出其中最小值为30，对应节点5。然后在weight数组中，找到5能直接到的节点（且对应mark也要为False），为4号和6号节点，且权重为20和60。此时判断dis[5]+20<dis[4]，结果成立，所以dis[4]更新为50。同理dis[6]被更新为90。

6）N==3时，找到所有Dis元素中，对应mark元素为False的元素。找出其中最小值为50，对应节点4。然后在weight数组中，找到4能直接到的节点（且对应mark也要为False），为6号节点，且权重为10。此时判断dis[4]+10<dis[6]，结果成立，所以dis[6]更新为60。

7）N==4时，找到所有Dis元素中，对应mark元素为False的元素。找出其中最小值为60，对应节点6。然后在weight数组中，找到6能直接到的节点（且对应mark也要为False），结果找不到6能直接到的节点。

8）N==5时，找到所有Dis元素中，对应mark元素为False的元素。找出其中最小值为max_int，对应节点2。然后在weight数组中，找到2能直接到的节点（且对应mark也要为False），为3号节点，且权重为5。此时判断dis[4]+10<dis[6]，结果不成立，不成立则不更新dis[3]。

9）N==6时，已经找到到对应mark为False的元素，直接break出循环。整个计算最短路径的过程结束。

10）可以看到N==6时得到Dis数组的结果是：[max_int,0,max_int,10,50,30,60]。除去index==0的元素，从1-6的元素，即是节点1到所有元素对应的距离（1到2的距离为max_int，说明没有路线）。

三、Python实现

import numpy as np
import sys

def dijkstra(start, graph_struct, node):
    """
    function:dijkstra
    args:
        start 要计算的起始点
        graph_struct 带权有向图的结构
        node 图中节点个数
    return:
        dis 元素为-1时，表示没有路径。其余为距离
    """
    # n表示有N个点，m表示M条边，x表示求那个点到所有点的最短路径
    n, m, x = node, len(graph_struct), start
    max_int = sys.maxsize
    weight = np.full([n + 1, n + 1], -1)
    dis = np.full(n + 1, max_int)
    # 初始化权重数组，自己到自己为0.其他为暂为-1
    for i in range(1, n + 1):
        weight[i][i] = 0

    for i in graph_struct:
        # 所有存在边的位置填上权重，没有关系的位置保持为-1，表示不可直接到达
        weight[i[0]][i[1]] = i[2]
        # 如果是与我们要求的x点相关的点，则也将x到i的权重填入dis列表中
        if i[0] == x:
            dis[i[1]] = i[2]

    # 程序走到这里，我们就有了权重数组 以及 dis数组（x到各个点的距离，如果没有边，则为max_int）
    # dis ： [max_int,  0,  max_int,  10,  max_int,  30,  100]， dis[0]不纳入计算，为了方便，我们只考虑index>=1的部分

    # 定义内部search函数，开始计算x到所有点的最短路径，最终更新到dis中
    def search(x, dis, weight, n):
        """
        function:search
        args:
            x 要求的点
            dis 距离数组
            weight 权重数组
            n 节点的个数
        return:dis
        """
        mark = np.full(n + 1, False)  # 创建一个mark数组，元素个数为n+1，[1,n]表示1-n点是否被当成最小值加过，已经加过为True，未被加过为False
        mark[x] = True  # 要求的点x，直接标记为加过
        dis[x] = 0  # 自己到自己的距离为0
        count = 1  # 当前已经加了几个点，当前只有x点，所以初始化为1

        # 开始循环，当count<=n时，说明还有点未被加过
        while count <= n:
            locate = 0  # locate记录计算出来马上要被加的点
            min = max_int  # 用于求最小值时比较用
            # 找到dis里面，还没有加过的位置(mark[idx]=False)里面数的最小值对应的index。
            # dis : [9223372036854775807 0 9223372036854775807 10 9223372036854775807 30 100]
            # mark : [False,True,False,False,False,False]，从中找出10的index为 3
            # 该for循环完毕后，min中的值就是最小值10
            for i in range(1, n + 1):
                if not mark[i] and dis[i] < min:
                    min = dis[i]
                    locate = i
            # 如果locate为0，则说明所有点都被加完了，直接退出循环
            if locate == 0: break
            # 如果locate不为0，说明找到了需要加的点，先对其进行标记
            mark[locate] = True
            # 加一个点count增1
            count += 1

            # 从我们找到的需要加的点locate（例如3）开始，看weight数组中他到各个点的距离
            for i in range(1, n + 1):
                # 如果某个点已经被加过了，我们就不计算locate到这个点的距离了
                # 如果locate到某个点的距离为-1，说明没有路，也不计算
                # 条件3：x到locate的距离（dis[locate]） + locate到点i的距离(weight[locate][i]) < x到i的距离 才能更新
                if not mark[i] and weight[locate][i] != -1 and (
                        dis[locate] + weight[locate][i] < dis[i]):
                    # 条件都满足，则计算，并更新dis中x-->i的距离
                    dis[i] = dis[locate] + weight[locate][i]

        return dis

    # 调用search开始计算x到各个点的距离，记录到dis数组中
    dis = search(x, dis, weight, n)

    # 打印dis数组
    for i in range(1, len(dis)):
        if dis[i] == max_int:
            dis[i] = -1
        print("%s点到%s点 %s" % (x, i, "的最短路径为%s" % dis[i] if dis[i] != max_int else '没有路'))

    # 返回
    return dis

if __name__ == '__main__':
    # 列举所有的边的权重，并写入weight列表
    weight_init = [(1, 3, 10), (1, 5, 30), (1, 6, 100), (2, 3, 5), (3, 4, 50), (4, 6, 10), (5, 6, 60), (5, 4, 20)]
    dis = dijkstra(1, weight_init, 6)

### Dijkstra算法原理还是比较简单的，但是使用代码实现的时候比较绕。需要多加复习，熟记于心。