计算几何-RC-poj2187

This article is made by Jason-Cow.
Welcome to reprint.
But please post the article's address.

今天学习一下旋(xuan1)转(zhuan3)卡(qia3)壳(qiao4)

1.凸包

2.对踵点

定理：最远点对必然属于对踵点对集合

对踵点定义：

        如果过凸包上的两个点可以画一对平行直线，使凸包上的所有点都

夹在两条平行线之间或落在平行线上，那么这两个点叫做一对对踵点。

具体有两种情况：

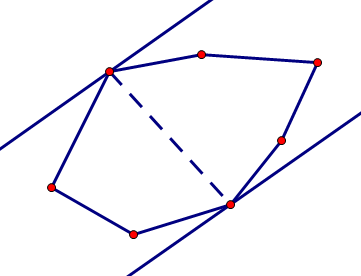
1.两个平行线正好卡着两个点

2.两个平行线分别卡着一条边和一个点

Rotating calipers Algorithm 是基于情况2的

        考虑到，固定一条边，凸包上的点到线的距离构成一个单峰函数，

所以，有“单调性”(姑且叫做单调性)

直观的感受一下

 

 

post the Rujia Liu 's words :

/*
    当Area(p[u], p[u+1], p[v+1]) <= Area(p[u], p[u+1], p[v])时停止旋转
    即Cross(p[u+1]-p[u], p[v+1]-p[u]) - Cross(p[u+1]-p[u], p[v]-p[u]) <= 0
    根据Cross(A,B) - Cross(A,C) = Cross(A,B-C)
    化简得Cross(p[u+1]-p[u], p[v+1]-p[v]) <= 0
*/

旋转code

 db RC(D*R,int n){//Rotating calipers
   R[]=R[n];// avoid to mod
   db ans=0.0;
   for(int u=,v=;u<n;u++){
     while(Cross(R[u+]-R[u],R[v+]-R[v])>)v=(v+)%n;
     ans=max(ans,Dis2(R[u],R[v]));
     ans=max(ans,Dis2(R[u+],R[v+]));
   }
   return ans;
 }

RC

一个小技巧，手写unique（其实是不会用STL，PS:不去重可以过）

 bl operator==(D A,D B){return (fabs(A.x-B.x)<eps && fabs(A.y-B.y)<eps);}

 void Unique(D*R,int&n){
   bl*In=new bl[n];
   for(int i=;i<=n;i++)if(R[i+]==R[i])In[i+]=;else In[i]=;
   int cnt=;
   for(int i=;i<=n;i++)if(!In[i])R[++cnt]=R[i];
   n=cnt;
 }

Unique

ACcode

 #include <algorithm>
 #include <iostream>
 #include <cstring>
 #include <cstdlib>
 #include <cstdio>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <map>
 #include <set>
 using namespace std;
 #define sqr(x) ((x)*(x))
 #define RG register
 #define op operator
 #define IL inline
 typedef double db;
 typedef bool bl;
 const db pi=acos(-1.0),eps=1e-;
 struct D{
   db x,y;
   D(db x=0.0,db y=0.0):x(x),y(y){}
 };
 typedef D V;
 bl operator<(D A,D B){return A.x<B.x||(A.x==B.x&&A.y<B.y);}
 bl operator==(D A,D B){return (fabs(A.x-B.x)<eps && fabs(A.y-B.y)<eps);}
 V operator+(V A,V B){return V(A.x+B.x,A.y+B.y);}
 V operator-(V A,V B){return V(A.x-B.x,A.y-B.y);}
 V operator*(V A,db N){return V(A.x*N,A.y*N);}
 V operator/(V A,db N){return V(A.x/N,A.y/N);}

 db Ang(db x){return(x*180.0/pi);}
 db Rad(db x){return(x*pi/180.0);}
 V Rotate(V A,db a){return V(A.x*cos(a)-A.y*sin(a),A.x*sin(a)+A.y*cos(a));}
 db Dis2(D A,D B){return sqr(A.x-B.x)+sqr(A.y-B.y);}
 db Dis(D A,D B){return sqrt(sqr(A.x-B.x)+sqr(A.y-B.y));}
 db Cross(V A,V B){return A.x*B.y-A.y*B.x;}
 db Dot(V A,V B){return A.x*B.x+A.y*B.y;}

 void Unique(D*R,int&n){
   bl*In=new bl[n];
   for(int i=;i<=n;i++)if(R[i+]==R[i])In[i+]=;else In[i]=;
   int cnt=;
   for(int i=;i<=n;i++)if(!In[i])R[++cnt]=R[i];
   n=cnt;
 }

 int Andrew(D*R,int&n,D*A){
   int m=;
   sort(R+,R+n+);
   Unique(R,n);
   for(int i=;i<=n;i++){
     while(m>= && Cross(A[m]-A[m-],R[i]-A[m-])<=)m--;
     A[++m]=R[i];
   }
   int k=m;
   for(int i=n-;i>=;i--){
     while(m>k  && Cross(A[m]-A[m-],R[i]-A[m-])<=)m--;
     A[++m]=R[i];
   }
   return n>?m-:m;
 }

 db RC(D*R,int n){    //Rotating calipers
   R[]=R[n];             // avoid to mod
   db ans=0.0;
   for(int u=,v=;u<n;u++){
     while(Cross(R[u+]-R[u],R[v+]-R[v])>)v=(v+)%n;
     ans=max(ans,Dis2(R[u],R[v]));
     ans=max(ans,Dis2(R[u+],R[v+]));
   }
   return ans;
 }

 const int MAXN=(int)4e5+;
 D R[MAXN],T[MAXN];

 int main(){
   int n;scanf("%d",&n);
   for(int i=;i<=n;i++)scanf("%lf%lf",&R[i].x,&R[i].y);
   int m=Andrew(R,n,T);
   printf("%.0lf\n",RC(T,m));
   return ;
 }