[集训]dance

题意

http://uoj.ac/problem/77

---

思考

显然能转化为最小割模型。若没有p_i的代价，则对于第i个格子，可以让源点连向第i个点，容量为黑色收益，再连向汇点，容量为白色收益。再考虑p_i的代价，对1~n的每个点新建一个哨兵节点，并向它连容量为pi的边。若前面存在点j落在当前区间中，再将哨兵节点连向点j，容量为正无穷。

但这样边数达到O(n^2)级别，不能接受。

发现哨兵节点所连的边对于ai来说都是一个连续的区间，可用主席树优化建图，边数将为O(nlogn)级别。

---

代码

 #pragma GCC optimize 2
 #include<bits/stdc++.h>
 using namespace std;
 typedef long long int ll;
 const ll inf=INT_MAX;
 int n;
 int head[*+],size=;
 int dfn[*],S,T;
 int what[],tmp[],Last[];
 ll valBoy[],valGirl[],a[],l[],r[],p[];
 struct edge
 {
     int to,next;
     ll w;
 }E[*+];
 inline ll max(ll x,ll y)
 {
     return x>y?x:y;
 }
 inline ll min(ll x,ll y)
 {
     return x<y?x:y;
 }
 inline void addEdge(int u,int v,ll w)
 {
     E[++size].to=v;
     E[size].next=head[u];
     E[size].w=w;
     head[u]=size;
 }
 inline void add(int u,int v,ll w)
 {
     addEdge(u,v,w);
     addEdge(v,u,);
 }
 bool bfs()
 {
     memset(dfn,-,sizeof(dfn));
     queue<int>Q;
     Q.push(S);
     dfn[S]=;
     while(!Q.empty())
     {
         int u=Q.front();
         Q.pop();
         for(int i=head[u];i;i=E[i].next)
         {
             int v=E[i].to;
             if(dfn[v]!=-||E[i].w==)
                 continue;
             dfn[v]=dfn[u]+;
             Q.push(v);
         }
     }
     return dfn[T]!=-;
 }
 ll dinic(int u,ll up)
 {
     if(u==T)
         return up;
     ll sum=;
     for(int i=head[u];i;i=E[i].next)
     {
         int v=E[i].to;
         if(dfn[v]!=dfn[u]+||E[i].w==)
             continue;
         ll g=dinic(v,min(E[i].w,up-sum));
         E[i].w-=g;
         E[i^].w+=g;
         sum+=g;
         if(g==)
             dfn[v]=-;
         if(sum==up)
             break;
     }
     return sum;
 }
 struct czyTree
 {
     int t[*],cur,root[],son[*][];
     int tot;
     void addPos(int pos,int l,int r,int&num,int pre,int from)
     {
         num=++tot;
         son[num][]=son[pre][],son[num][]=son[pre][];
         if(l==r)
         {
             add(num+T,from,inf);
             if(Last[pos])
                 add(num+T,Last[pos]+T,inf);
             Last[pos]=num;
             return;
         }
         int mid=(l+r)>>;
         if(pos<=mid)
             addPos(pos,l,mid,son[num][],son[pre][],from);
         else
             addPos(pos,mid+,r,son[num][],son[pre][],from);
         if(son[num][])
             add(num+T,son[num][]+T,inf);
         if(son[num][])
             add(num+T,son[num][]+T,inf);
     }
     void addS(int L,int R,int l,int r,int num,int from)
     {
         if(!num)
             return;
         if(L<=l&&r<=R)
         {
             add(from,num+T,inf);
             return;
         }
         int mid=(l+r)>>;
         if(R<=mid)
             addS(L,R,l,mid,son[num][],from);
         else if(mid<L)
             addS(L,R,mid+,r,son[num][],from);
         else
             addS(L,R,l,mid,son[num][],from),addS(L,R,mid+,r,son[num][],from);
     }
 }Tree;
 int main()
 {
     ios::sync_with_stdio(false);
     cin>>n;
     int tot=;
     for(int i=;i<=n;++i)
     {
         cin>>a[i]>>valBoy[i]>>valGirl[i]>>l[i]>>r[i]>>p[i];
         tmp[++tot]=a[i];
     }
     sort(tmp+,tmp+tot+);
 //    tot=unique(tmp+1,tmp+tot+1)-tmp-1;
     S=,T=*n+;
     for(int i=;i<=n;++i)
     {
         add(S,i,valBoy[i]);
         add(i,T,valGirl[i]);
         add(i,i+n,p[i]);
     }
     for(int i=;i<=n;++i)
     {
         int L=,R=tot;
         while(tmp[L]<l[i]&&L<=tot)
             ++L;
         while(r[i]<tmp[R]&&R)
             --R;
         Tree.addS(L,R,,tot,Tree.root[i-],i+n);
         Tree.addPos(lower_bound(tmp+,tmp+tot+,a[i])-tmp,,tot,Tree.root[i],Tree.root[i-],i);
     }
     ll ans=;
     while(bfs())
         ans+=dinic(S,inf);
     for(int i=;i<=n;++i)
         ans-=valBoy[i]+valGirl[i];
     cout<<-ans<<endl;
     return ;
 }

---

细节

如下图所示，若此题使用dinic，左右两个建图方式是不等价的，且左图是正确的，右图是错误的，并且右图的最小割结果会变小。（假设有很多蓝色边）

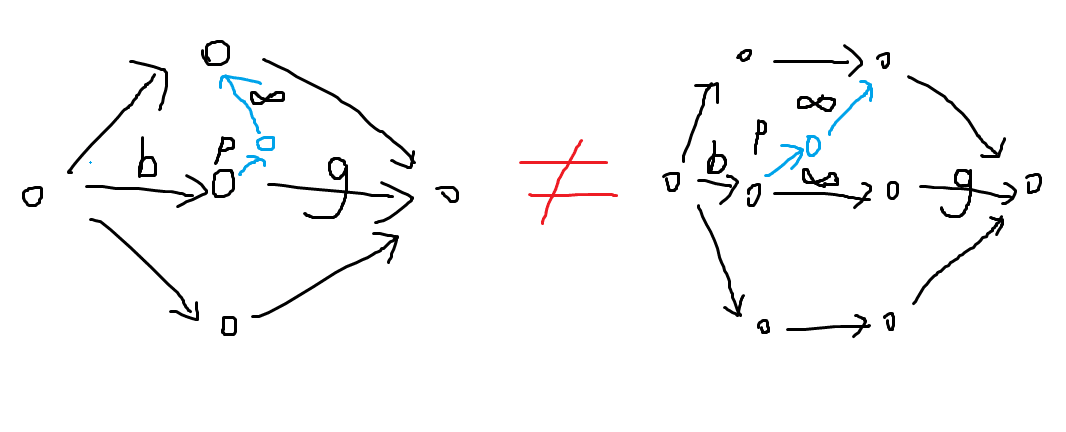
事实上，哨兵节点连出的边必须连在左边一排点上。

考虑下图所示情况。在dinic中，若先走了红色路径，则无法经过蓝色路径。原因是蓝色正无穷边此时不存在反向边，蓝色路径不连通。这样，最小割就少了一些流量。

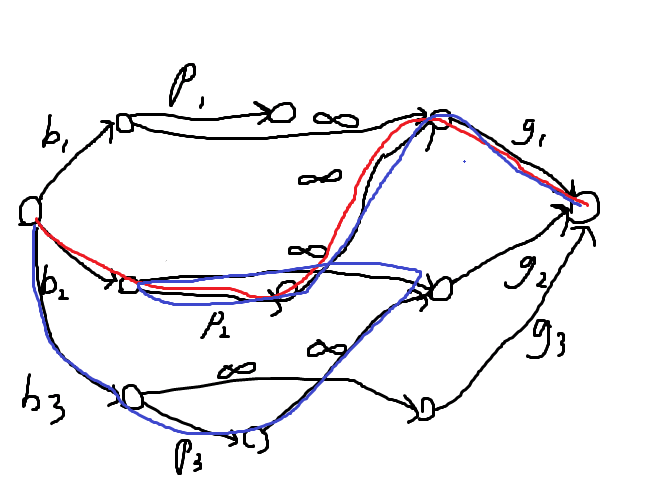
此外，在主席树建图中，要注意相同a_i的点要连向前一个相同a_i的点。

(CORRECTED BY CZY)