loj6247 九个太阳

题意：

k<=2^20,n<=10^15.

标程：

 #include<cstdio>
 using namespace std;
 typedef long long ll;
 const int mod=;
 const int root=;
 ll wn,w,ans,l,n,k;
 ll ksm(ll x,ll y)
 {
     ll res=;
     while (y) {if (y&) res=res*x%mod; x=x*x%mod; y>>=;}
     return res;
 }
 int main()
 {
     scanf("%lld%lld",&n,&k);
     l=-__builtin_clz(k);w=ksm(root,<<-l);wn=;
     for (int i=;i<k;i++)
       ans=(ans+ksm(+wn,n))%mod,wn=wn*w%mod;
     printf("%lld\n",ans*ksm(k,mod-)%mod);
     return ;
 }

题解：二项式定理+原根

当k=1的时候，Ans=sigma(C(n,i))=(1+x)^n=2^n.

当k=2的时候，将x=-1代入，将两个式子加起来/2就是Ans。(1^j+(-1)^j)/2

当k=4的时候……我们可以仿照fft的奇偶分组过程，给每个项一个系数，当k|i,第i项的系数为1。

原根（n次单位根）可以解决！得到如下判定式：

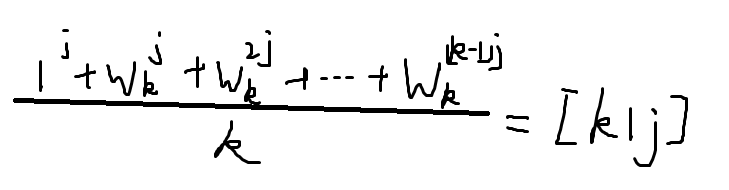
运用对复根的二项式定理可以化简答案式：

O(klogn)。