矩阵matrix

矩阵matrix

1. 矩阵matrix

1.1. 定义
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵，简称m × n矩阵。记作：

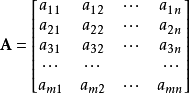
这m×n 个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n，m×n矩阵A也记作Amn。
元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵 [8]  。

符号A ∈ Rm×n表示一个m行n列的矩阵，并且矩阵A中的所有元素都是实数。
符号x ∈ Rn表示一个含有n个元素的向量。通常，我们把n维向量看成是一个n行1列矩阵，即列向量。如果我们想表示一个行向量（1行n列矩阵），我们通常写作xT (xT表示x的转置，后面会解释它的定义)。

用aj 或A:，j表示A矩阵的第j列元素：

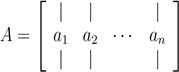
用aT i或 Ai，:表示矩阵的第i行元素:

1.2. 基本运算
矩阵的基本运算包括矩阵的加法，减法，数乘，转置，共轭和共轭转置。

加法

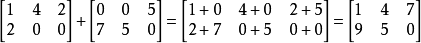
矩阵的加法满足下列运算律(A，B，C都是同型矩阵)：

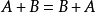
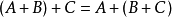
应该注意的是只有同型矩阵之间才可以进行加法。

减法

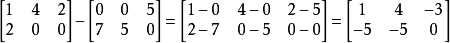
数乘

矩阵的数乘满足以下运算律：

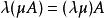
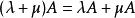
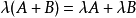
矩阵的加减法和矩阵的数乘合称矩阵的线性运算 [8]  。

转置
把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵（ ），这一过程称为矩阵的转置

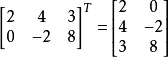
矩阵的转置满足以下运算律：

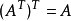
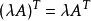
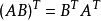
乘法
两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵，它们的乘积C是一个m×p矩阵
  ，它的一个元素：

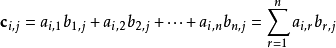
并将此乘积记为:

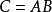
例如：

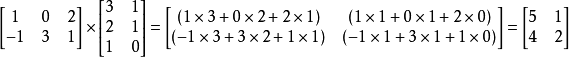
矩阵的乘法满足以下运算律：

结合律：
 

左分配律：

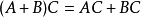
右分配律：

 

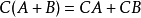
矩阵乘法不满足交换律。