网络知识02:TCP/IP概述

一 DOD模型

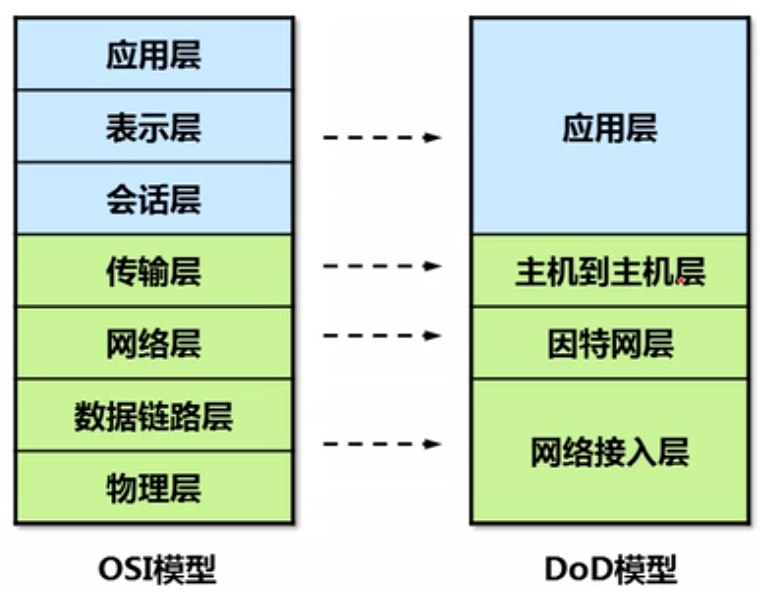
传输控制协议IRI特网协议(TCP/IP)组是由美国国防部(DOD)所创建的,主要用来确保数据的完整性及在毁灭性战争中保持通信

是由一组不同功能的协议组合在一起的协议簇

利用一组协议完成OSI所实现的功能

二 DOD模型的协议

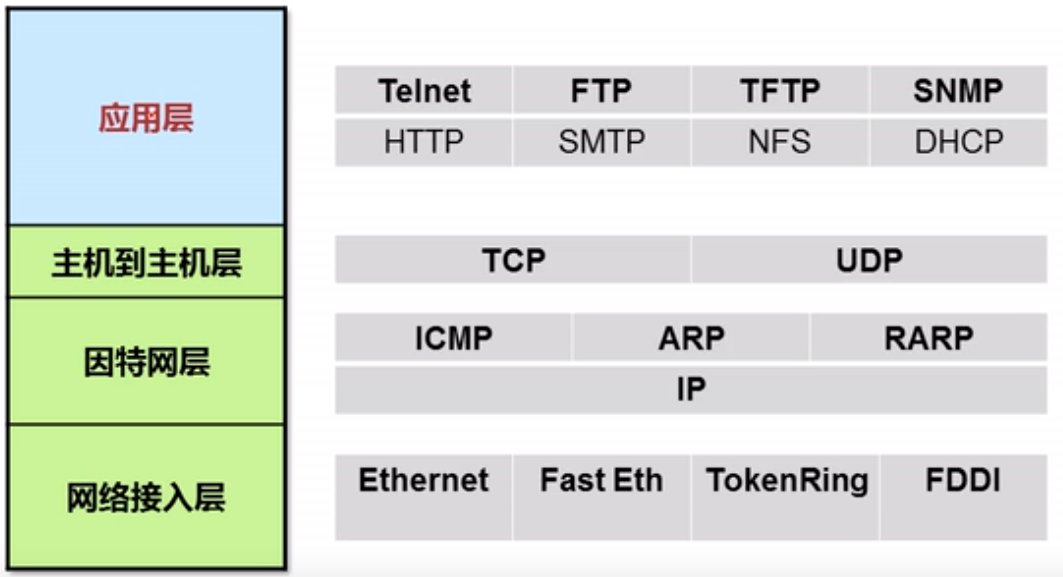
应用层:Telent(远程登陆协议,提供远程管理服务,端口23),FTP(文件传输协议,提供互联网文件资源共享服务,端口20,21),TFTP(简单文件传输协议,提供简单的文件传输服务,UDP协议,端口69),SNMP,HTTP,SMPT(简单邮件传输协议,提供互联网电子邮件服务,端口号25),POP3(邮局协议,提供互联网电子邮件服务),NFS,DHCP

主机到主机层:TCP,UDP

因特网层:负责将分组的报文从源端发到目的端

网络接入层:Ethernet,FastEth,TokenRing,FDDI

三 TCP/IP协议

TCP:传输控制协议,属于面向连接的网络协议,可靠传输,流控

使用的应用:Web浏览器,电子邮件,文件传输程序

3.1 TCP的报文结构

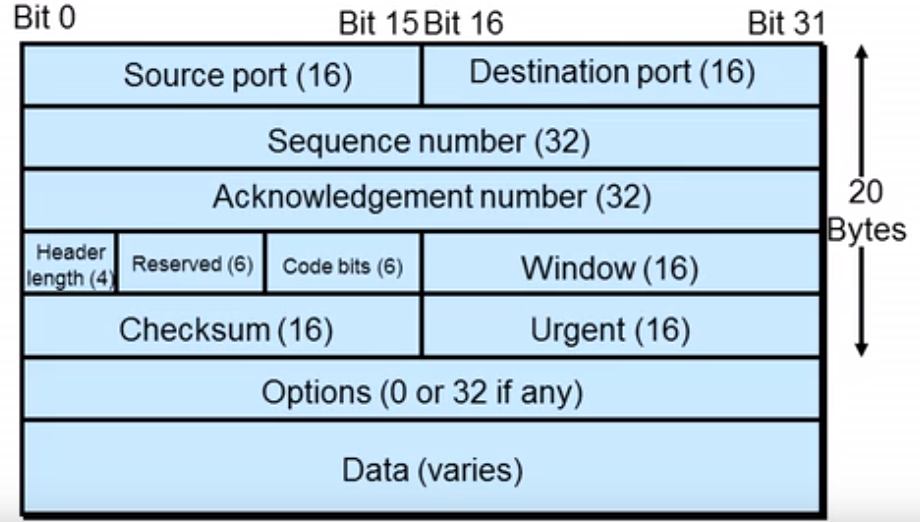
详细报文

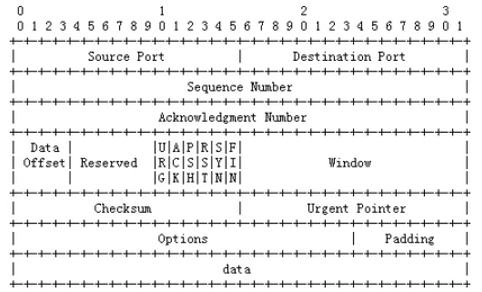
3.2 UDP协议

用户报文协议,属于无连接的网络协议,不可靠传输,尽力传递

使用UDP的应用:域名系统DNS;视频流;IP语音(VoIP)

UDP头部

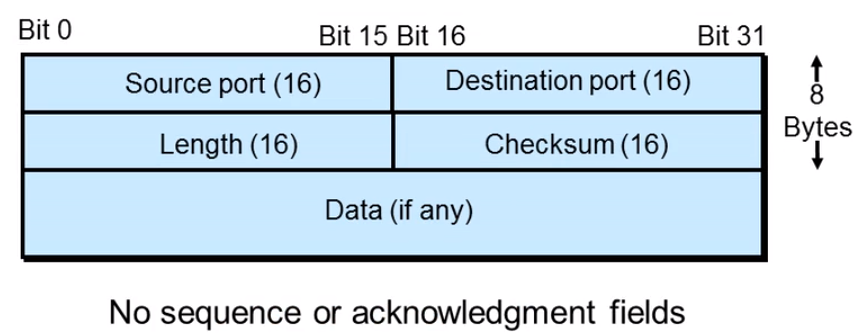
3.3 端口号

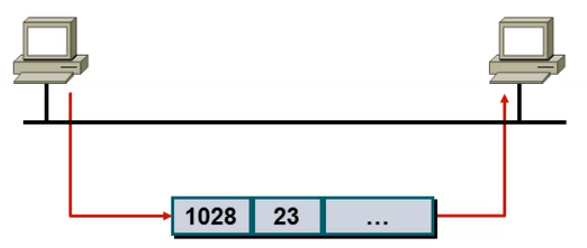
源端口随机分配,目标端口使用已知端口

应用客户端使用的源端口号一般为系统中未使用的且大于1023

目的端口号为服务器应用服务的进程.如telent为23

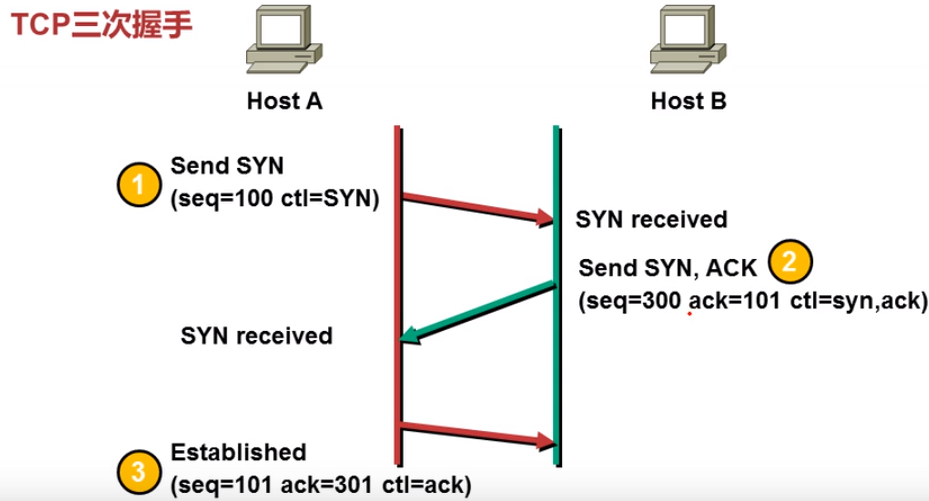
3.4 TCP的三次握手

加入两台主机进行连接,过程如下

１．A产生一个序列号,加入是100,带上这个序列号,向B发送一个SYN请求

２．B收到这个请求，如果确认连接，也会使用一个序列号ｓｅｑ，假如是３００，就会带上自己的序列号的ＳＹＮ请求，以及在对方序列号加一形成的ＡＣＫ号确认发送给对方

３．Ａ收到B的确认号和请求的ｓｅｑ连接后，也会发送一个ａｃｋ确认号，连接建立

3.5 端口号的连接

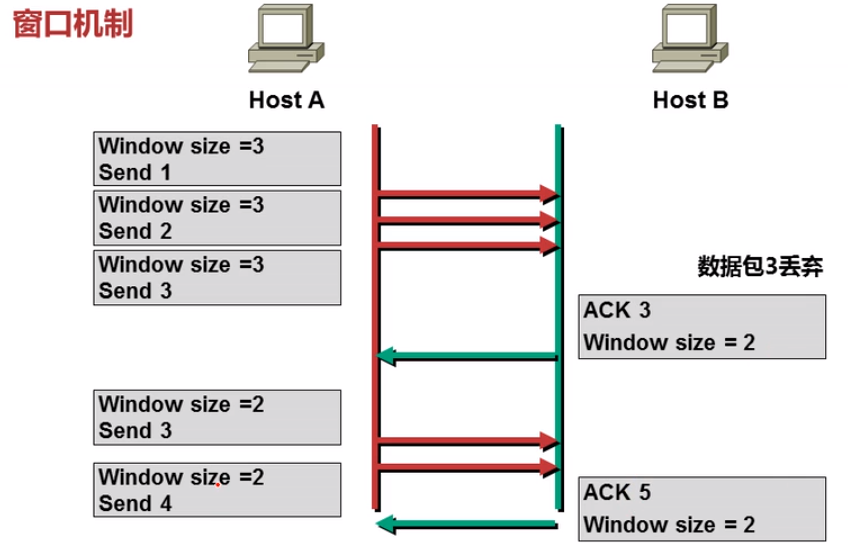
3.6 窗口机制

窗口机制是一种可靠的机制，加入AB主机进行会话连接,发送数据包,一开始A发了三个数据包,这是B没有处理完成,把数据包3丢弃,同时发送ACK为3,同时发送自己希望发送的的包的大小是2,这时A就会知道B的处理能力,会每次发送2个大小为2的包,连接一直进行

3.7 因特网层机制

负责将分组的报文从源端发到目的端

协议:ICMP,ARP,RARP,IP

网络层的作用：

为数据中的设备提供逻辑地址

负责数据包的寻径和转发

IP报文

ARP协议:

将IPv4地址解析为MAC地址

维护映射的缓存

查询arp的方式:arp -a

最开始没有arp表,会先发送一个广播的请求报文,写有IP,但是MAC地址时所有地址,是一个广播帧,在局域网内都会收到这个广播,非对应IP,不会处理,对应的IP会回应一个回应报文,,就会把MAC地址缓存在ARP表中

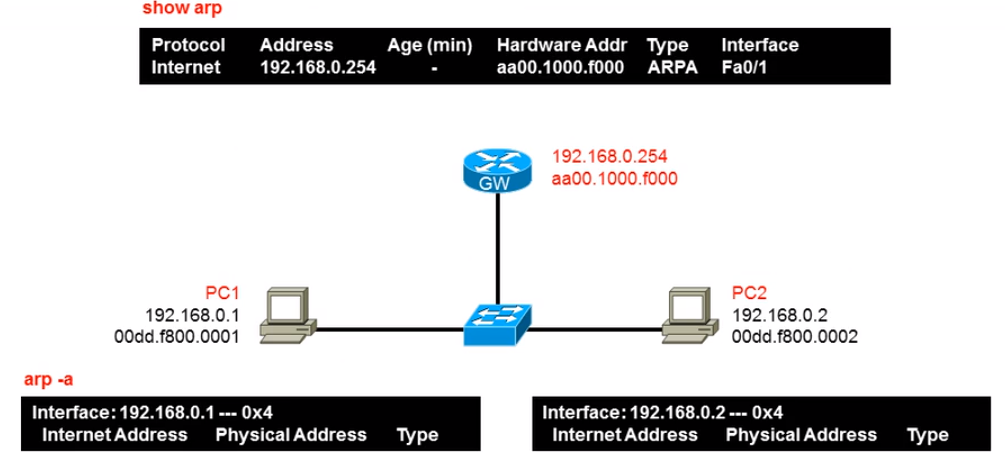
arp的一个请求报文

回应报文

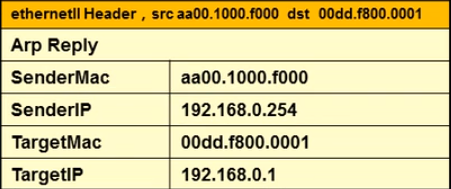
经过一系列arp请求,都会有自己的arp表,并维护

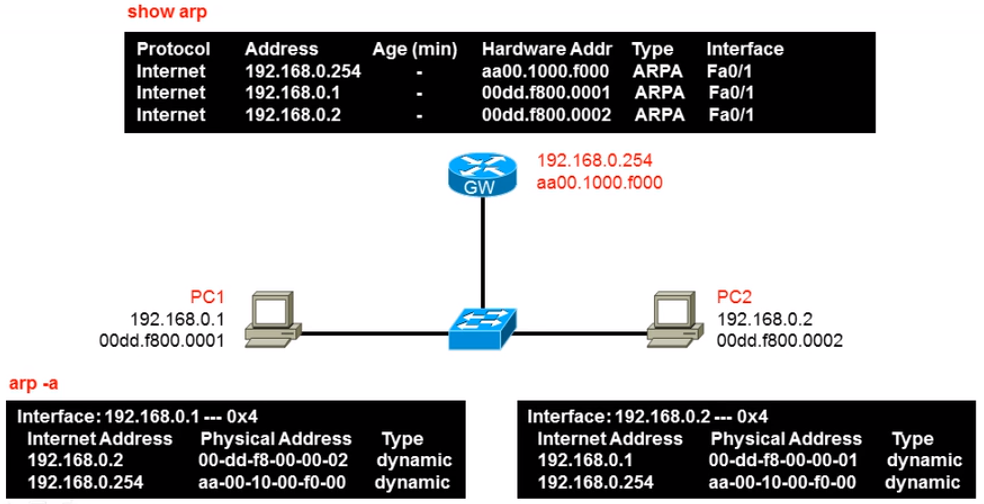
四 VLSM

可变长度的子网掩码

4.1 IP地址

IPv4,32位,点分十进制

路由器只关心网络部份

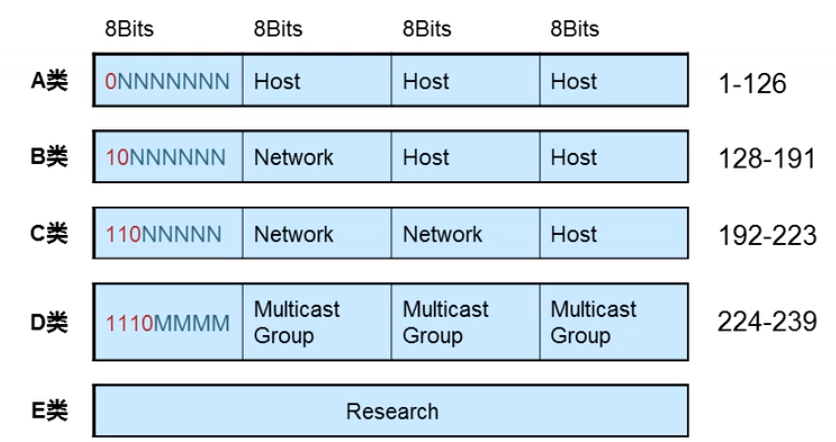
IP=网络部分+主机部分

通信类型:单播,广播,组播

IP地址类型:

IP=网络部分+主机部分

网络地址:指代网络的地址.在网络的IPv4地址范围内,最小地址保留为网络地址.此地址的主机部分的每个主机均为0.

广播地址:用于向网络中的所有主机发送数据的特殊地址.广播地址使用该网络范围内的最大地址.即主机部分的个比特位全部为1的地址

主机地址:分配给网络中终端设备的地址

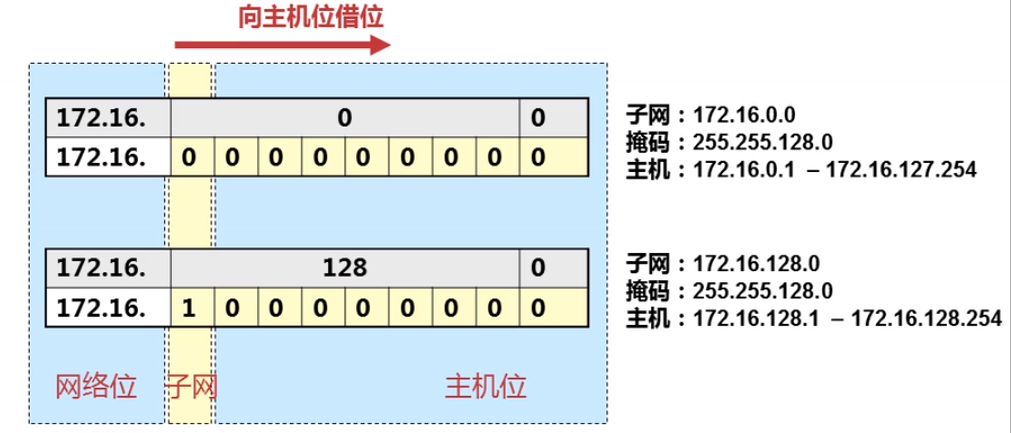
4.2 划分子网

掩码的作用:划分网络位和主机位

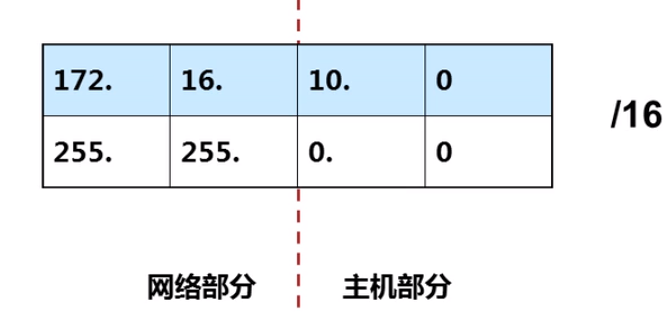
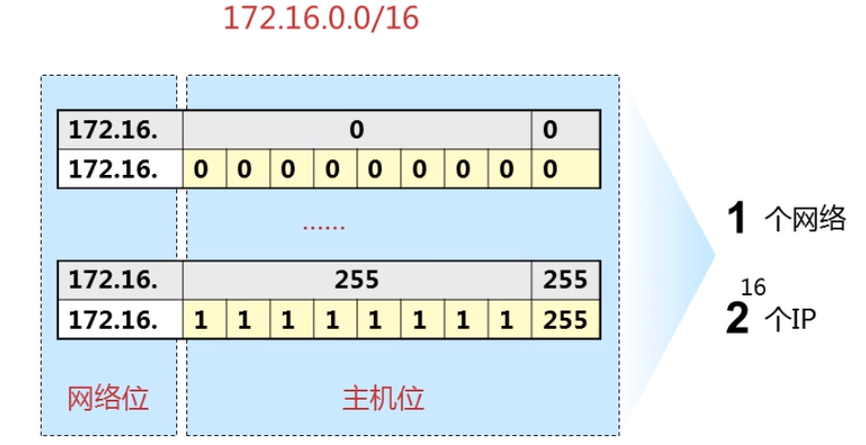
向主机借位划分

4.3 私有地址

10.0.0.0 to 10.255.255.255(10.0.0.0/8)

172.16.0.0 to 172.31.255.255(172.16.0.0/12)

192.168.0.0 to 192.168.255.255(192.168.0.0/16)

参考连接

公开课视频:https://www.bilibili.com/video/av24400474/?p=3