回顾 Monty Hall （三门问题）

一、问题描述

Monty Hall Problem 源于美国的一档电视节目《Let's Make a Deal》，其中Monty Hall 是这个节目的主持人。
节目中有三扇门1、2、3，其中有一扇门后面放着一辆汽车，另外两扇门后面是山羊，玩家只能选择一扇门，并赢得门后面的礼物。
游戏开始，你随机选择一扇门，假如为门1，然后主持人会从剩余两扇门中打开一扇后面是山羊的门，比如为门3。现在主持人问：为了赢得车，是否要改选门2（另外一扇没有被打开的门）？

二、现实打脸

直觉是剩下两扇门分别对应一辆车和一只山羊，所以选到车的概率是1/2，换不换都一样。

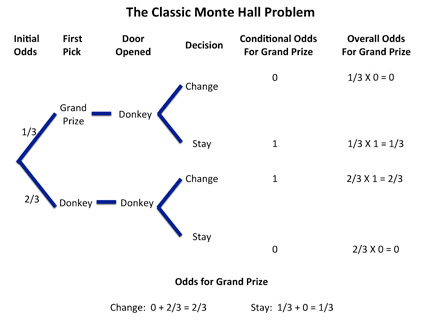
但如果分情况讨论，

可见换门的胜率为2/3，应该要换门。上图没有把主持人开门的步骤写出来，这里再补充一个，

到这里可能就明白了，问题就出在主持人知道门背后的情况，并且他总是会给你展示有羊的门（总不能给你展示有车的门吧）。

换个角度想，由于你只能选择一扇门，因此胜率是1/3，主持人拥有两扇门，他的胜率就是2/3，因为主持人总是能给你展示一道有羊的门，所以即便他给你展示了有羊的门，他的组合胜率依然是2/3。

现在给你一个机会换成一个胜率为2/3的组合，肯定要啊。

三、数学证明

事件A：你选择了有车的门
事件B：主持人选择了有羊的门

根据贝叶斯公式，
\[
P\{A|B\} = \frac{P\{A\}P\{B|A\}}{P\{B\}}
\]

可以确定 P{A}=1/3，然而不确定主持人是否了解门后的情况，因此 P{B|A}、p{B} 要分情况讨论：

情况一：主持人不知道门后的情况，开门的行为是随机的：

于是 P{B|A}=1，p{B}=2/3，那么 p{A}=1/2。换不换都一样。

情况二：主持人知道门后的情况，他肯定开一扇有山羊的门：

于是 P{B|A}=1，p{B}=1，那么 p{A}=1/3。换门胜算更大。

四、参考

Monty Hall 问题