Pytorch 之 backward

首先看这个自动求导的参数：

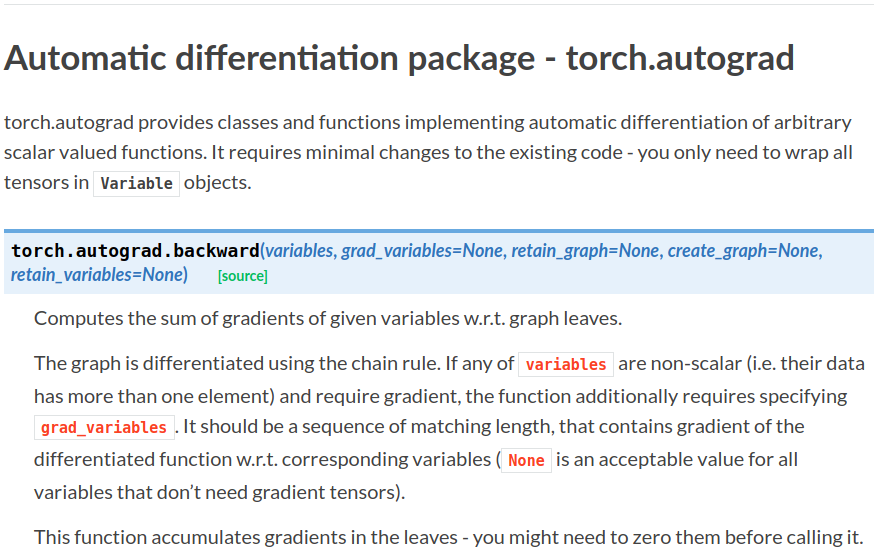
• grad_variables：形状与variable一致，对于y.backward()，grad_variables相当于链式法则dz/dx=dz/dy × dy/dx 中的 dz/dy。grad_variables也可以是tensor或序列。
• retain_graph：反向传播需要缓存一些中间结果，反向传播之后，这些缓存就被清空，可通过指定这个参数不清空缓存，用来多次反向传播。
• create_graph：对反向传播过程再次构建计算图，可通过backward of backward实现求高阶导数。

注意variables 和 grad_variables 都可以是 sequence。对于scalar（标量，一维向量）来说可以不用填写grad_variables参数，若填写的话就相当于系数。若variables非标量则必须填写grad_variables参数。下面结合参考示例来解释一下这个参数怎么用。

先说一下自己总结的一个通式，适用于所有形式：

      对于此式，x的梯度x.grad为 

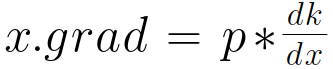
1.scalar标量

注意参数requires_grad=True让其成为一个叶子节点，具有求导功能。

手动求导结果：

代码实现：

import torch as t
from torch.autograd import Variable as v

a = v(t.FloatTensor([2, 3]), requires_grad=True)    # 注意这里为一维，标量
b = a + 3
c = b * b * 3
out = c.mean()
out.backward(retain_graph=True) # 这里可以不带参数，默认值为‘1’，由于下面我们还要求导，故加上retain_graph=True选项

结果：

a.grad
Out[184]:
Variable containing:
  15  
  18
[torch.FloatTensor of size 1x2]

结果与手动计算一样

backward带参数呢？此时的参数为系数

将梯度置零：

a.grad.data.zero_()

再次求导验证输入参数仅作为系数：

n.backward(torch.Tensor([[2,3]]), retain_graph=True)

结果：（2和3应该分别作为系数相乘）

a.grad
Out[196]:
Variable containing:
  30
  54
[torch.FloatTensor of size 1x2]

验证了我们的想法。

2.张量

import torch
from torch.autograd import Variable as V

m = V(torch.FloatTensor([[2, 3]]), requires_grad=True)   # 注意这里有两层括号，非标量
n = V(torch.zeros(1, 2))
n[0, 0] = m[0, 0] ** 2
n[0, 1] = m[0, 1] ** 3

求导 ：（此时的[[1, 1]]为系数，仅仅作为简单乘法的系数），注意 retain_graph=True，下面我们还要求导，故置为True。

n.backward(torch.Tensor([[1,1]])， retain_graph=True)

结果：

m.grad
Out[184]:
Variable containing:
  4  27
[torch.FloatTensor of size 1x2]

将梯度置零：

m.grad.data.zero_()

再次求导验证输入参数仅作为系数：

n.backward(torch.Tensor([[2,3]]))

结果：4,27 × 2,3 =8,81  验证了系数这一说法

 m.grad
Out[196]:
Variable containing:
  8  81
[torch.FloatTensor of size 1x2]

注意backward参数，由于是非标量，不填写参数将会报错。

3.  另一种重要情形

之前我们求导都相当于是loss对于x的求导，没有接触中间过程。然而对于下面的链式法则我们知道如果知道中间的导数结果，也可以直接计算对于输入的导数。而grad_variables参数在某种意义上就是中间结果。即上面都是z.backward()之类，那么考虑y.backward(b) 或 y.backward(x)是什么意思呢？

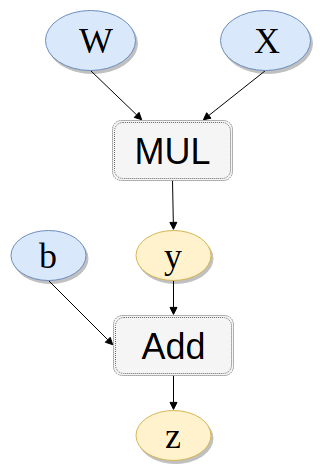
下面给出一个例子解释清楚：

import torch
from torch.autograd import Variable
x = Variable(torch.randn(3), requires_grad=True)
y = Variable(torch.randn(3), requires_grad=True)
z = Variable(torch.randn(3), requires_grad=True)
print(x)
print(y)
print(z)

t = x + y
l = t.dot(z)

结果：

# x
Variable containing:
 0.9168
 1.3483
 0.4293
[torch.FloatTensor of size 3]

# y
Variable containing:
 0.4982
 0.7672
 1.5884
[torch.FloatTensor of size 3]

# z
Variable containing:
 0.1352
-0.4037
-0.2425
[torch.FloatTensor of size 3]

在调用 backward 之前，可以先手动求一下导数，应该是： 

当我们打印x.grad和y.grad时都是 x.grad = y.grad = z。 当我们打印z.grad 时为 z.grad = t = x + y。这里都没有问题。重要的来了：

先置零：

x.grad.data.zero_()
y.grad.data.zero_()
z.grad.data.zero_()

看看下面这个情况：

t.backward(z)
print(x.grad)
print(y.grad)
print(z.grad)

此时的结果为：

x和y的导数仍然与上面一样为z。而z的导数为0。解释：
t.backward(z): 若求x.grad: z * dt/dx   即为dl/dt × dt/dx=z

               若求y.grad: z * dt/dy   即为dl/dt × dt/dy=z

               若求z.grad: z * dt/dz   即为dl/dt × dt/dz = z×0 = 0

再验证一下我们的想法：

清零后看看下面这种情况：

t.backward(x)
print(x.grad)
print(y.grad)
print(z.grad)

x和y的导数仍然相等为x。而z的导数为0。解释：
t.backward(x): 若求x.grad: x * dt/dx   即为x × 1 = x

               若求y.grad: x * dt/dy   即为x × 1 = x

               若求z.grad: x * dt/dz   即为x × 0 = 0
验证成功。

另：k.backward(p)接受的参数p必须要和k的大小一样。这一点也可以从通式看出来。

参考：

PyTorch 的 backward 为什么有一个 grad_variables 参数？

PyTorch 中文网

PyTorch中的backward [转]

Calculus on Computational Graphs: Backpropagation