第七十五课 图的遍历（DFS）

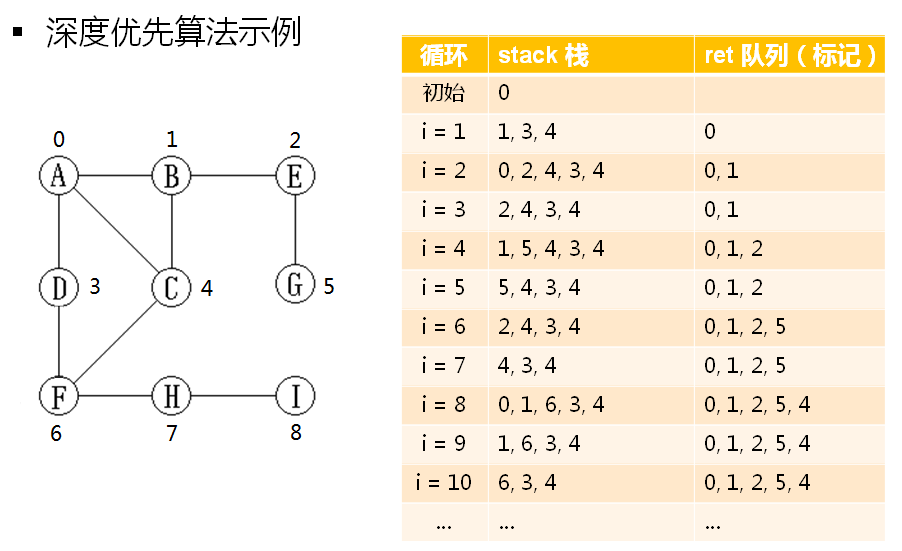
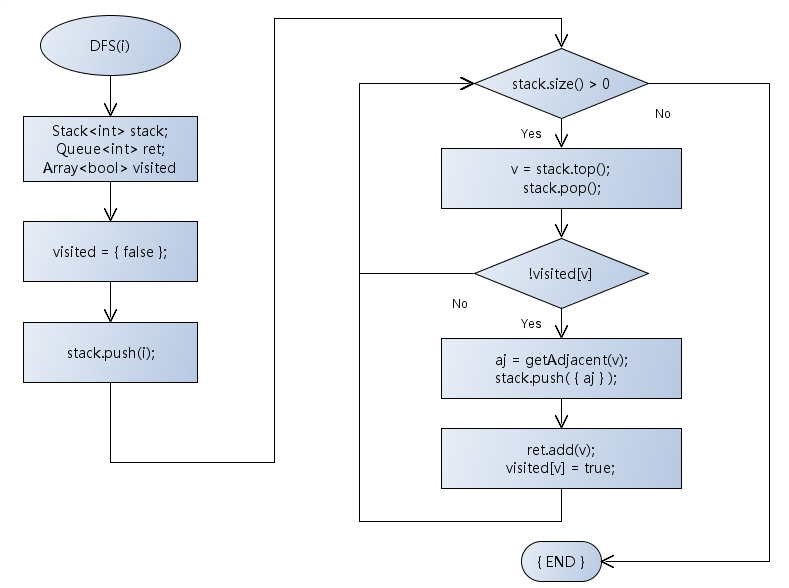
添加DFS函数：

 #ifndef GRAPH_H
 #define GRAPH_H

 #include "Object.h"
 #include "SharedPointer.h"
 #include "Array.h"
 #include "DynamicArray.h"
 #include "LinkQueue.h"
 #include "LinkStack.h"

 namespace DTLib
 {

 template < typename E >
 struct Edge : public Object
 {
     int b;
     int e;
     E data;

     Edge(int i=-, int j=-)
     {
         b = i;
         e = j;
     }

     Edge(int i, int j, const E& value)
     {
         b = i;
         e = j;
         data = value;
     }

     bool operator == (const Edge<E>& obj)
     {
         return (b == obj.b) && (e == obj.e);  //在这里不关注权值大小
     }

     bool operator != (const Edge<E>& obj)
     {
         return !(*this == obj);
     }
 };

 template < typename V, typename E >
 class Graph : public Object
 {
 protected:
     template < typename T >
     DynamicArray<T>* toArray(LinkQueue<T>& queue)
     {
         DynamicArray<T>* ret = new DynamicArray<T>(queue.length());

         if( ret != NULL )
         {
             for(int i=; i<ret->length(); i++, queue.remove())
             {
                 ret->set(i, queue.front());
             }
         }
         else
         {
             THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create ret object...");
         }

         return ret;
     }
 public:
     virtual V getVertex(int i) = ;
     virtual bool getVertex(int i, V& value) = ;
     virtual bool setVertex(int i, const V& value) = ;
     virtual SharedPointer< Array<int> > getAdjacent(int i) = ;
     virtual E getEdge(int i, int j) = ;
     virtual bool getEdge(int i, int j, E& value) = ;
     virtual bool setEdge(int i, int j, const E& value) = ;
     virtual bool removeEdge(int i, int j) = ;
     virtual int vCount() = ;
     virtual int eCount() = ;
     virtual int OD(int i) = ;
     virtual int ID(int i) = ;
     virtual int TD(int i)
     {
         return ID(i) + OD(i);
     }

     SharedPointer< Array<int> > BFS(int i)
     {
         DynamicArray<int>* ret = NULL;

         if( ( <= i) && (i < vCount()) )
         {
             LinkQueue<int> q;
             LinkQueue<int> r;
             DynamicArray<bool> visited(vCount());

             for(int i=; i<visited.length(); i++)
             {
                 visited[i] = false;
             }

             q.add(i);

             while( q.length() >  )
             {
                 int v = q.front();

                 q.remove();

                 if( !visited[v] )
                 {
                     SharedPointer< Array<int> > aj = getAdjacent(v);

                     for(int j=; j<aj->length(); j++)
                     {
                         q.add((*aj)[j]);
                     }

                     r.add(v);

                     visited[v] = true;
                 }
             }

             ret = toArray(r);
         }
         else
         {
             THROW_EXCEPTION(InvalidParameterException, "Index i is invalid...");
         }

         return ret;
     }

     SharedPointer< Array<int> > DFS(int i)
     {
         DynamicArray<int>* ret = NULL;

         if( ( <= i) && (i < vCount()) )
         {
             LinkStack<int> s;
             LinkQueue<int> r;
             DynamicArray<bool> visited(vCount());

             for(int j=; j<visited.length(); j++)
             {
                 visited[j] = false;
             }

             s.push(i);

             while( s.size() >  )
             {
                 int v = s.top();

                 s.pop();

                 if( !visited[v] )
                 {
                     SharedPointer< Array<int> > aj = getAdjacent(v);

                     for(int j=aj->length() - ; j>=; j--)
                     {
                         s.push((*aj)[j]);
                     }

                     r.add(v);

                     visited[v] = true;
                 }
             }

             ret = toArray(r);
         }
         else
         {
             THROW_EXCEPTION(InvalidParameterException, "Index i is invalid...");
         }

         return ret;
     }
 };

 }

 #endif // GRAPH_H

测试程序如下：

 #include <iostream>
 #include "BTreeNode.h"
 #include "ListGraph.h"
 #include "MatrixGraph.h"

 using namespace std;
 using namespace DTLib;

 int main()
 {
     MatrixGraph<, char, int> g;
     const char* VD = "ABEDCGFHI";

     for(int i=; i<; i++)
     {
         g.setVertex(, VD[i]);
     }

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     SharedPointer< Array<int> > sa = g.DFS();

     for(int i=; i<sa->length(); i++)
     {
         cout << (*sa)[i] << " ";
     }

     cout << endl;

     return ;
 }

结果如下：

深度优先的思想就是二叉树的先序遍历思想。

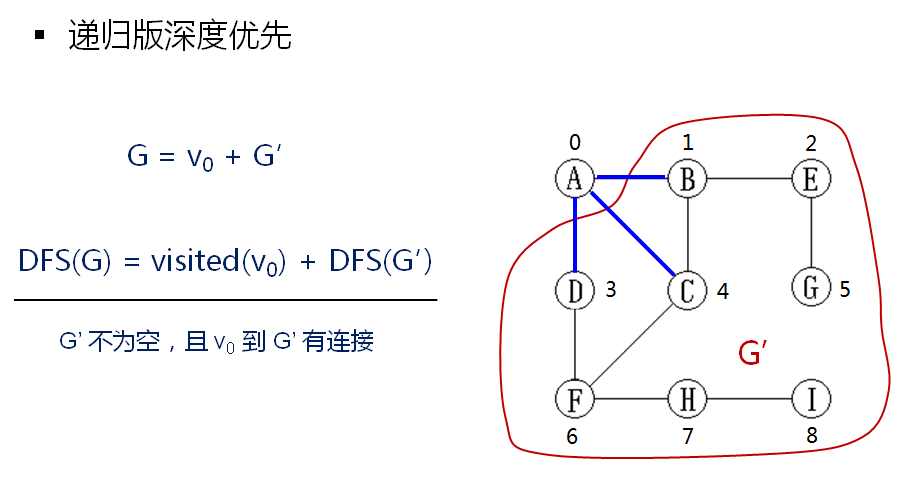
递归版的深入优先算法如下：

 #include <iostream>
 #include "BTreeNode.h"
 #include "ListGraph.h"
 #include "MatrixGraph.h"

 using namespace std;
 using namespace DTLib;

 template < typename V, typename E>
 void DFS(Graph<V, E>& g, int v, Array<bool>& visited)
 {
     if( ( <= v) && (v < g.vCount()) )
     {
         cout << v << endl;

         visited[v] = true;

         SharedPointer< Array<int> > aj = g.getAdjacent(v);

         for(int i=; i<aj->length(); i++)
         {
             if( !visited[(*aj)[i]] )
             {
                 DFS(g, (*aj)[i], visited);
             }
         }
     }
     else
     {
         THROW_EXCEPTION(InvalidParameterException, "Index v is invalid...");
     }
 }

 template < typename V, typename E >
 void DFS(Graph<V, E>& g, int v)
 {
     DynamicArray<bool> visited(g.vCount());

     for(int i=; i<visited.length(); i++)
     {
         visited[i] = false;
     }

     DFS(g, v, visited);
 }

 int main()
 {
     MatrixGraph<, char, int> g;
     const char* VD = "ABEDCGFHI";

     for(int i=; i<; i++)
     {
         g.setVertex(, VD[i]);
     }

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     SharedPointer< Array<int> > sa = g.DFS();

     for(int i=; i<sa->length(); i++)
     {
         cout << (*sa)[i] << " ";
     }

     cout << endl;

     DFS(g, );

     return ;
 }

结果如下：

小结：