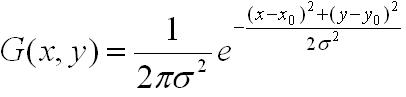Sift中尺度空间、高斯金字塔、差分金字塔(DOG金字塔)、图像金字塔
转自:https://blog.csdn.net/dcrmg/article/details/52561656
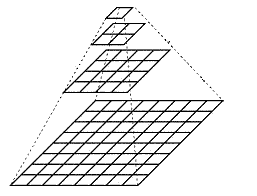
一、 图像金字塔
图像金字塔是一种以多分辨率来解释图像的结构,通过对原始图像进行多尺度像素采样的方式,生成N个不同分辨率的图像。把具有最高级别分辨率的图像放在底部,以金字塔形状排列,往上是一系列像素(尺寸)逐渐降低的图像,一直到金字塔的顶部只包含一个像素点的图像,这就构成了传统意义上的图像金字塔。
获得图像金字塔一般包括二个步骤:
1. 利用低通滤波器平滑图像
2. 对平滑图像进行抽样(采样)
有两种采样方式——上采样(分辨率逐级升高)和下采样(分辨率逐级降低)
上采样:
下采样:
二、高斯金字塔
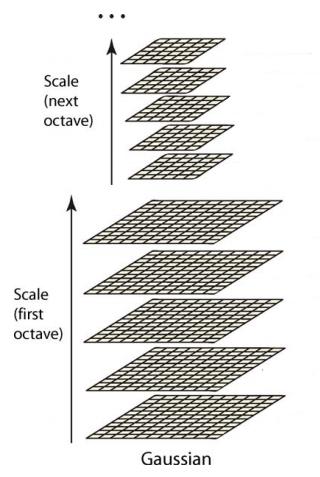
高斯金字塔式在Sift算子中提出来的概念,首先高斯金字塔并不是一个金字塔,而是有很多组(Octave)金字塔构成,并且每组金字塔都包含若干层(Interval)。
高斯金字塔构建过程:
1. 先将原图像扩大一倍之后作为高斯金字塔的第1组第1层,将第1组第1层图像经高斯卷积(其实就是高斯平滑或称高斯滤波)之后作为第1组金字塔的第2层,高斯卷积函数为:
对于参数σ,在Sift算子中取的是固定值1.6。
2. 将σ乘以一个比例系数k,等到一个新的平滑因子σ=k*σ,用它来平滑第1组第2层图像,结果图像作为第3层。
3. 如此这般重复,最后得到L层图像,在同一组中,每一层图像的尺寸都是一样的,只是平滑系数不一样。它们对应的平滑系数分别为:0,σ,kσ,k^2σ,k^3σ……k^(L-2)σ。
4. 将第1组倒数第三层图像作比例因子为2的降采样,得到的图像作为第2组的第1层,然后对第2组的第1层图像做平滑因子为σ的高斯平滑,得到第2组的第2层,就像步骤2中一样,如此得到第2组的L层图像,同组内它们的尺寸是一样的,对应的平滑系数分别为:0,σ,kσ,k^2σ,k^3σ……k^(L-2)σ。但是在尺寸方面第2组是第1组图像的一半。
这样反复执行,就可以得到一共O组,每组L层,共计O*L个图像,这些图像一起就构成了高斯金字塔,结构如下:
在同一组内,不同层图像的尺寸是一样的,后一层图像的高斯平滑因子σ是前一层图像平滑因子的k倍;
在不同组内,后一组第一个图像是前一组倒数第三个图像的二分之一采样,图像大小是前一组的一半;
高斯金字塔图像效果如下,分别是第1组的4层和第2组的4层:

三、 尺度空间
图像的尺度空间解决的问题是如何对图像在所有尺度下描述的问题。
在高斯金字塔中一共生成O组L层不同尺度的图像,这两个量合起来(O,L)就构成了高斯金字塔的尺度空间,也就是说以高斯金字塔的组O作为二维坐标系的一个坐标,不同层L作为另一个坐标,则给定的一组坐标(O,L)就可以唯一确定高斯金字塔中的一幅图像。
尺度空间的形象表述:
上图中尺度空间中k前的系数n表示的是第一组图像尺寸是当前组图像尺寸的n倍。
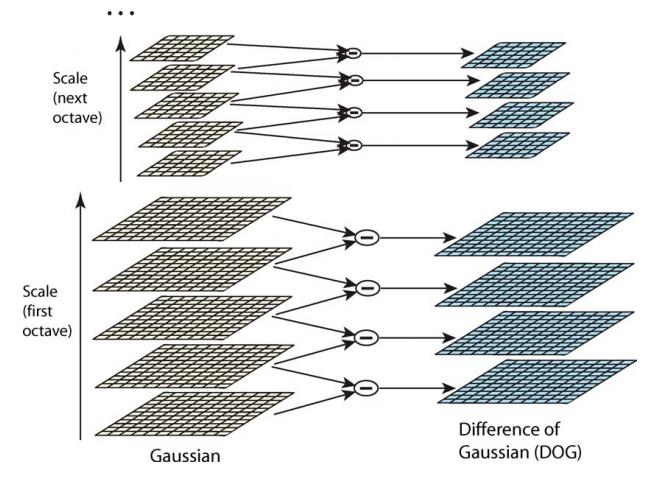
四、 DOG金字塔
差分金字塔,DOG(Difference
of Gaussian)金字塔是在高斯金字塔的基础上构建起来的,其实生成高斯金字塔的目的就是为了构建DOG金字塔。
DOG金字塔的第1组第1层是由高斯金字塔的第1组第2层减第1组第1层得到的。以此类推,逐组逐层生成每一个差分图像,所有差分图像构成差分金字塔。概括为DOG金字塔的第o组第l层图像是有高斯金字塔的第o组第l+1层减第o组第l层得到的。
DOG金字塔的构建可以用下图描述:
每一组在层数上,DOG金字塔比高斯金字塔少一层。后续Sift特征点的提取都是在DOG金字塔上进行的。
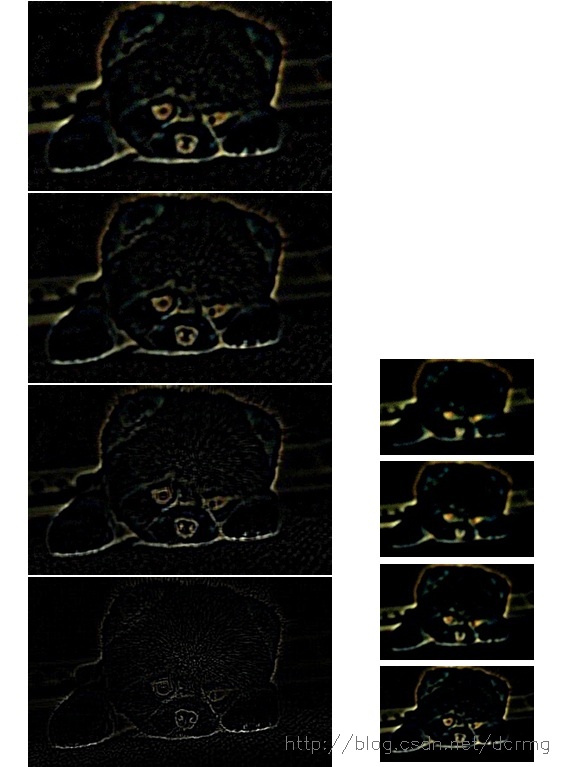
DOG金字塔的显示效果如下:
这些长得黑乎乎的图像就是差分金字塔的实际显示效果,只在第1组第1层差分图像上模糊可以看到一个轮廓。但其实这里边包含了大量特征点信息,只是我们人眼已经分辨不出来了。
下边对这些DOG图像进行归一化,可有很明显的看到差分图像所蕴含的特征,并且有一些特征是在不同模糊程度、不同尺度下都存在的,这些特征正是Sift所要提取的“稳定”特征:
Sift中尺度空间、高斯金字塔、差分金字塔(DOG金字塔)、图像金字塔的更多相关文章
- 图像金字塔、高斯金字塔、差分金字塔(DOG金字塔)、尺度空间、DoG (Difference of Gaussian)角点检测
[图像金字塔] 图像金字塔是一种以多分辨率来解释图像的结构,通过对原始图像进行多尺度像素采样的方式,生成N个不同分辨率的图像.把具有最高级别分辨率的图像放在底部,以金字塔形状排列,往上是一系列像素(尺 ...
- 图像金字塔及其在 OpenCV 中的应用范例(上)
前言 图像金字塔是计算机图形学中非常重要的一个概念. 本文将详细介绍这个概念,以及它的实现与应用. 图像金字塔的定义 图像金字塔是一组图像的集合,集合中的所有图像都是通过对某一图像连续降采样得到的一组 ...
- Atitit 图像金字塔原理与概率 attilax的理解总结qb23
Atitit 图像金字塔原理与概率 attilax的理解总结qb23 1.1. 高斯金字塔 ( Gaussianpyramid): 拉普拉斯金字塔 (Laplacianpyramid):1 1.2 ...
- OpenCV图像金字塔
图像金字塔 目标 本文档尝试解答如下问题: 如何使用OpenCV函数 pyrUp 和 pyrDown 对图像进行向上和向下采样. 原理 Note 以下内容来自于Bradski和Kaehler的大作: ...
- SIFT中的尺度空间和传统图像金字塔
SIFT中的尺度空间和传统图像金字塔 http://www.zhizhihu.com/html/y2010/2146.html 最近自己混淆了好多概念,一边弄明白的同时,也做了一些记录,分享一下.最近 ...
- 【OpenCV】SIFT原理与源码分析:DoG尺度空间构造
原文地址:http://blog.csdn.net/xiaowei_cqu/article/details/8067881 尺度空间理论 自然界中的物体随着观测尺度不同有不同的表现形态.例如我们形 ...
- 图像金字塔(pyramid)与 SIFT 图像特征提取(feature extractor)
David Lowe(SIFT 的提出者) 0. 图像金字塔变换(matlab) matlab 对图像金字塔变换接口的支持(impyramid),十分简单好用. 其支持在reduce和expand两种 ...
- DoG 、Laplacian、图像金字塔详解
DoG(Difference of Gaussian) DoG (Difference of Gaussian)是灰度图像增强和角点检测的方法,其做法较简单,证明较复杂,具体讲解如下: Differe ...
- 【计算机视觉】SIFT中LoG和DoG比较
<SIFT原理与源码分析>系列文章索引:http://www.cnblogs.com/tianyalu/p/5467813.html 在实际计算时,三种方法计算的金字塔组数noctaves ...
随机推荐
- 洛谷试炼场-简单数学问题-P1045 麦森数-高精度快速幂
洛谷试炼场-简单数学问题 B--P1045 麦森数 Description 形如2^P−1的素数称为麦森数,这时P一定也是个素数.但反过来不一定,即如果PP是个素数,2^P-1 不一定也是素数.到19 ...
- authentication plugin caching_sha2
操作系统:windows 10 mysql版本:mysql Ver 8.0.11 for Win64 on x86_64 (MySQL Community Server - GPL) 安装完mysq ...
- [No0000E1]C# 关键字
关键字是 C# 编译器预定义的保留字.这些关键字不能用作标识符,但是,如果您想使用这些关键字作为标识符,可以在关键字前面加上 @ 字符作为前缀. 在 C# 中,有些标识符在代码的上下文中有特殊的意义, ...
- app相关的一些网站
https://www.qimai.cn 排名排行关键字原aso100
- java设计模式--单例
GOF23(group of four)---由4个大牛总结的JAVA23种常用的设计模式,归根结底都是为了代码的可扩展性. 设计模式中一种比较重要的思想就是:开闭原则,尽量做到对扩展开放,对修改关闭 ...
- struts2 中 paramsPrepareParamsStack 拦截器
struts2二次参数拦截器内容: 规定了请求的执行顺序 在struts2中,其拦截器为框架精华部分,而二次参数拦截器paramsPrepareParamsStack 对于解决数据回显,对象修改属性 ...
- Installing Precise (12.04.2) using netboot onto a Marvell ArmadaXP Development Board
https://wiki.ubuntu.com/ARM/Server/Install https://wiki.ubuntu.com/ARM/Server/Install/ArmadaXP Arm ...
- jvisualvm All-in-One Java Troubleshooting Tool
java 监控.故障.性能可视化分析 VisualVM: Download https://visualvm.github.io/download.html All-in-One Java Troub ...
- EF-CodeFirst-基础
什么是Code-First Code-First主要用于领域驱动设计.在Code-First方法中,专注于应用程序的域,先开始为域实体创建类,而不是先设计数据库,然后创建与数据库设计相匹配的类.下图说 ...
- 重读《深入理解Java虚拟机》二、Java如何分配和回收内存?Java垃圾收集器如何工作?
线程私有的内存区域随用户线程的结束而回收,内存分配编译期已确定,内存分配和回收具有确定性.共享线程随虚拟机的启动.结束而建立和销毁,在运行期进行动态分配.垃圾收集器主要对共享内存区域(堆和方法区)进行 ...