洛谷 P3373 【模板】线段树 2

洛谷 P3373 【模板】线段树 2

洛谷传送门

题目描述

如题，已知一个数列，你需要进行下面三种操作：

• 将某区间每一个数乘上 xx
• 将某区间每一个数加上 xx
• 求出某区间每一个数的和

输入格式

第一行包含三个整数 n,m,pn,m,p，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含 nn 个用空格分隔的整数，其中第 ii 个数字表示数列第 ii 项的初始值。

接下来 mm 行每行包含若干个整数，表示一个操作，具体如下：

操作 11： 格式：1 x y k 含义：将区间 [x,y][x,y] 内每个数乘上 kk

操作 22： 格式：2 x y k 含义：将区间 [x,y][x,y] 内每个数加上 kk

操作 33： 格式：3 x y 含义：输出区间 [x,y][x,y] 内每个数的和对 pp 取模所得的结果

输出格式

输出包含若干行整数，即为所有操作 33 的结果。

输入输出样例

输入 #1复制

输出 #1复制

说明/提示

【数据范围】

对于 30%30% 的数据：n \le 8n≤8，m \le 10m≤10

对于 70%70% 的数据：n \le 10^3n≤103，m \le 10^4m≤104

对于 100%100% 的数据：n \le 10^5n≤105，m \le 10^5m≤105

除样例外，p = 571373p=571373

（数据已经过加强^_）

样例说明：

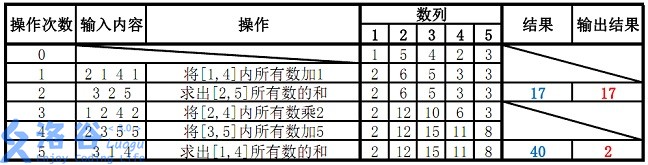
故输出应为 1717、22（ 40 \bmod 38 = 240mod38=2 ）

题解：

线段树模板维护区间乘和区间加，查询区间和。

如果对于简单线段树不是很了解的同学可以翻看本蒟蒻的这篇博客：

详解简单线段树

但是简单线段树并没有给出区间乘法的维护方法...

但我们可以参照区间加法进行类比。区间加法需要维护一个延迟标记，区间乘法当然也需要，由于乘法就是一连串的加法，所以我们在下传延迟标记的时候不仅需要下传乘法标记给线段树数组和子节点的乘法标记数组，还要把乘法标记下传给加法标记数组。也就是说：

线段树维护区间乘法的步骤为：

线段树数组乘标记，自己乘标记，加法数组乘标记。

加法的直接上简单线段树的板子即可。

注意，先乘后加！

代码：

#include<cstdio>
#define int long long
#define lson pos<<1
#define rson pos<<1|1
using namespace std;
const int maxn=1e5+10;
int n,m,mod;
int a[maxn];
int tree[maxn<<2],lazy[maxn<<2],lazy2[maxn<<2];
void build(int pos,int l,int r)
{
    int mid=(l+r)>>1;
    if(l==r)
    {
        tree[pos]=a[l];
        return;
    }
    build(lson,l,mid);
    build(rson,mid+1,r);
    tree[pos]=(tree[lson]+tree[rson])%mod;
}
void mark(int pos,int l,int r,int k,int flag)
{
    if(flag)
    {
        tree[pos]=(tree[pos]*k)%mod;
        lazy2[pos]=(lazy2[pos]*k)%mod;
        lazy[pos]=(lazy[pos]*k)%mod;
    }
    else
    {
        tree[pos]=(tree[pos]+(r-l+1)*k)%mod;
        lazy2[pos]=(lazy2[pos]+k)%mod;
    }
}
void pushdown(int pos,int l,int r)
{
    int mid=(l+r)>>1;
    mark(lson,l,mid,lazy[pos],1);
    mark(rson,mid+1,r,lazy[pos],1);
    mark(lson,l,mid,lazy2[pos],0);
    mark(rson,mid+1,r,lazy2[pos],0);
    lazy2[pos]=0,lazy[pos]=1;
}
void update(int pos,int l,int r,int x,int y,int k,int flag)
{
    int mid=(l+r)>>1;
    if(x<=l && r<=y)
    {
        if(flag)
            mark(pos,l,r,k,flag);
        else
            mark(pos,l,r,k,flag);
        return;
    }
    pushdown(pos,l,r);
    if(x<=mid)
        update(lson,l,mid,x,y,k,flag);
    if(y>mid)
        update(rson,mid+1,r,x,y,k,flag);
    tree[pos]=(tree[lson]+tree[rson])%mod;
}
int query(int pos,int l,int r,int x,int y)
{
    int ret=0;
    int mid=(l+r)>>1;
    if(x<=l && r<=y)
        return tree[pos]%mod;
    pushdown(pos,l,r);
    if(x<=mid)
        ret=(ret+query(lson,l,mid,x,y))%mod;
    if(y>mid)
        ret=(ret+query(rson,mid+1,r,x,y))%mod;
    return ret%mod;
}
signed main()
{
    for(int i=1;i<=maxn<<2;i++)
        lazy[i]=1,lazy2[i]=0;
    scanf("%lld%lld%lld",&n,&m,&mod);
    for(int i=1;i<=n;i++)
        scanf("%lld",&a[i]);
    build(1,1,n);
    for(int i=1;i<=m;i++)
    {
        int opt,x,y,k;
        scanf("%lld",&opt);
        if(opt==1)
        {
            scanf("%lld%lld%lld",&x,&y,&k);
            update(1,1,n,x,y,k,1);
        }
        else if(opt==2)
        {
            scanf("%lld%lld%lld",&x,&y,&k);
            update(1,1,n,x,y,k,0);
        }
        else
        {
            scanf("%lld%lld",&x,&y);
            printf("%lld\n",query(1,1,n,x,y));
        }
    }
    return 0;
}