Leetcode 5. Longest Palindromic Substring(最长回文子串， Manacher算法)

Leetcode 5. Longest Palindromic Substring(最长回文子串， Manacher算法)

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.

Example 2:

Input: "cbbd"
Output: "bb"

题解:

这个题重新学习了Manacher算法，重新研读第一次学习的代码，真正把这个题的思路想清楚，就可以按照理解很快的把代码实现出来，比我第一次学习这个算法的时候看懂别人的代码然后把别人的模板抄下来，进步了很多。

这个题给我的启发也是，学习任何算法，思考清楚整个过程然后再自己实现它，思考的过程长一点，理解好每个细节是很重要的，只有想明白才能很快把代码写出来！以后要养成没有思考清楚就不着急下手敲题的习惯。

Manacher算法：是一个很典型的空间换时间的算法，给出我初次学习的笔记https://www.cnblogs.com/shanyr/p/5676597.html

　　重新梳理以下这个算法：

　　算法主要分为三部分：

　　A. 扩展原字符串：

　　　　a.为了防止遍历到起始位置的时候会出现越界的情况，在最开始添加字符“$”(我是用手动判度是否到到结尾的，如果不加这个判断我感觉也可以在结尾加一个‘$’)

　　　　b.将每个字符用未出现过的字符隔开，一般用‘#’

　　     根据前两步，一个字符串会变成下面的形式

　　　　b a b a d

　　     ->$#b#a#b#a#d#

　　B. 变量定义：

　　　　a.定义p[i]表示从第i个位置可以向两边延伸的最长的位置，使得以i为中心，左右各扩展p[i]长度的子串满足回文

　　　　　例如对串$#b#a#b#a#d#的p数组为

　　　　　       $ #  b # a  # b  # a # d #

　　　　p  ->  0  0 1  0 3  0 3  0 1 0  1 0

　　　　　然后可以发现p中的最大值就是最长回文子串的长度，很容易证明。但是这个题要求输出的是子串，只要从最大值为中心，前后p[]的位置搜索，把不是'#'输出就可以。

　　C. 求p[i]:由于我们是O（n）的算法，所以在计算第i个位置的时候，前面的i-1个位置的p值已经算出来了。

　　　　我们可以利用之前求的对称性：定义mx为当前扫描的最远的位置，id为mx对应的中心点，可以将p[i]分成两种情况求解：

　　　　a. 情况1，如下图所示，mx-i >p[j],那么p[i]一定等于p[j]。（因为id左右mx是对称的）

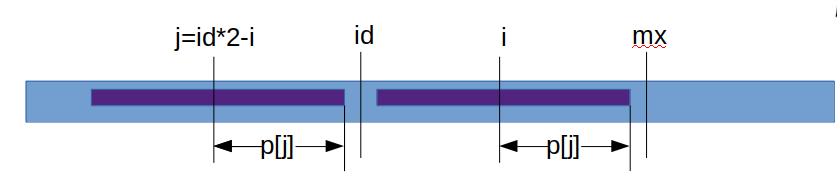
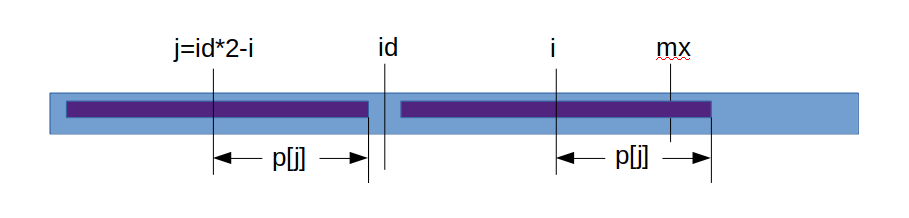
　　　　b.情况2，如下图所示，mx-i <= p[j],那么mx-i的长度的部分一定是对称的，但是超出的部分就要挨个判断了，判断结束后要更新mx = i+p[i], id = i。（因为id左右mx是对称的）

　

给出代码:

 class Solution {
 public:
     string longestPalindrome(string s) {
         //扩展
         string expend_s;
         expend_s+='$';
         int len = s.length();
         for(int i = ; i < len; i++){
             expend_s+='#';
             expend_s+=s[i];
         }
         expend_s+='#';
         //定义
         int p[*expend_s.length()];
         memset(p,,sizeof(p));
         int mx = , id = ;
         int max = , maxid = ;//保存最大回味子串搜索长度和位置
         //求p
         for(int i = ; i < expend_s.length(); i++){
             int j = *id - i;
             if(p[j]<mx-i){
                 p[i] = p[j];
             }
             else{
                 for(;expend_s[i+p[i]]==expend_s[i-p[i]]; p[i]++){
                     if(i+p[i]>=expend_s.length())break;//要判断右侧是否越界
                 }
                 mx = i+p[i];
                 id = i;
             }
             if(max < p[i]){
                 max = p[i];
                 maxid = i;
             }
         }
         string ans;
         for(int i = maxid-max+; i <= maxid+max-; i++){
             if(expend_s[i]!='#'){
                 ans+=expend_s[i];
             }
         }
         return ans;
     }
 };