MIT线性代数：17.正交矩阵和Cram-Schmidt正交化的更多相关文章

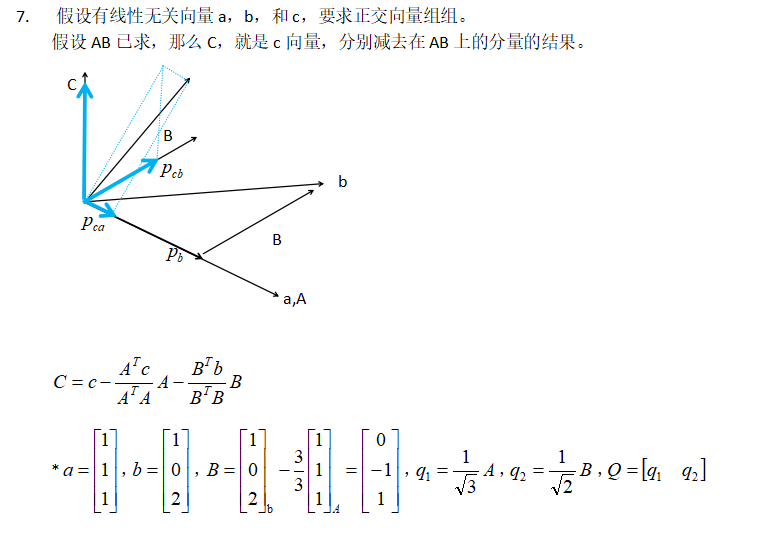
  1. 线性代数之——正交矩阵和 Gram-Schmidt 正交化

    这部分我们有两个目标.一是了解正交性是怎么让 \(\hat x\) .\(p\) .\(P\) 的计算变得简单的,这种情况下,\(A^TA\) 将会是一个对角矩阵.二是学会怎么从原始向量中构建出正交向 ...

  2. MIT线性代数课程 总结与理解-第一部分

    概述 个人认为线性代数从三个角度,或者说三个工具来阐述了线性关系,分别是: 向量 矩阵 空间 这三个工具有各自的一套方法,而彼此之间又存在这密切的联系,通过这些抽象出来的工具可以用来干一些实际的活,最 ...

  3. MIT线性代数：22.对角化和A的幂

  4. MIT线性代数：21.特征值和特征向量

  5. MIT线性代数：20.克拉默法则，逆矩阵和体积

  6. MIT线性代数：19.行列式和代数余子式

  7. MIT线性代数：18.行列式及其特性

  8. MIT线性代数：16.投影矩阵和最小二乘

  9. MIT线性代数：15.子空间的投影

随机推荐

  1. linux下搭建nginx+mysql+apache

    对于开发人员来说,进行Web开发时可以用Apache进行网站测试,然而当一个Web程序进行发布时,Apache中并发性能差就显得很突出,这时配置一台Nginx服务器显得尤为重要. 以下是配置Nginx ...

  2. HTML5 原生拖放

    前言: HTML5提供专门的拖拽与拖放的API,可以方便的指定某个元素可拖动,可以创建自定义的可拖动元素和放置目标 相关知识点: 1.拖放事件 拖放元素时,将依次触发下列事件 dragstart  按 ...

  3. MongoDB 学习笔记之 Aggregation Pipeline

    Aggregation Pipeline: 常用操作符介绍: $project:包含.排除.重命名和显示字段 $match:查询,需要同find()一样的参数 $limit:限制结果数量 $skip: ...

  4. python语言程序设计基础（嵩天）第三章课后习题部分个人练习

    p69: *题3.5: 源代码: (1)print(30-3**2+8//3**2*10)     答案:21 (2)print(3*4**2/8%5)     答案:1.0 (3)print(2** ...

  5. JPG和PNG特性分析及适用范围

    个人博客: http://mcchen.club JPG的特性   ----有损压缩 1.支持摄影图像或写实图像的高级压缩,并且可利用压缩比例控制图像文件大小. 2.有损压缩会使图像数据质量下降,并且 ...

  6. django-Xadmin后台管理

    0919自我总结 django-Xadmin后台管理 一.安装环境 pip install https://codeload.github.com/sshwsfc/xadmin/zip/django2 ...

  7. drf框架序列化和返序列化

    0903自我总结 drf框架序列化和反序列化 from rest_framework import serializers 一.自己对于序列化和反序列化使用的分类 前后端交互主要有get,post,p ...

  8. Win10安装虚拟机 + Ubuntu

    近期需要利用虚拟机,同时在虚拟机中安装Ubuntu系统.整理安装过程,供今后学习参考. 虚拟机安装包:VMware-workstation-full-12.1.0 链接:https://pan.bai ...

  9. Python之反射机制

    什么是反射? 1.有时我们要访问某个变量或是方法时并不知道到底有没有这个变量或方法,所以就要做些判断.判断是否存在字符串对应的变量及方法.2.我们知道访问变量时是不能加引号的,否则会被当成字符串处理. ...

  10. 详解Java Web项目启动执行顺序

    一. web.xml加载过程(步骤): 启动web项目,容器(如Tomcat.Apache)会去读取它的配置文件web.xml 中的两个节点,context-param和listener. 紧接着,容 ...