PCA降维的原理、方法、以及python实现。

参考：菜菜的sklearn教学之降维算法.pdf!!

PCA(主成分分析法)

1. PCA(最大化方差定义或者最小化投影误差定义)是一种无监督算法，也就是我们不需要标签也能对数据做降维，这就使得其应用范围更加广泛了。那么PCA的核心思想是什么呢？

• 例如D维变量构成的数据集，PCA的目标是将数据投影到维度为K的子空间中，要求K<D且最大化投影数据的方差。这里的K值既可以指定，也可以利用主成分的信息来确定。
• PCA其实就是方差与协方差的运用。
• 降维的优化目标：将一组 N 维向量降为 K 维，其目标是选择 K 个单位正交基，使得原始数据变换到这组基上后，各变量两两间协方差为 0，而变量方差则尽可能大（在正交的约束下，取最大的 K 个方差）。

2. PCA存在的问题：

• 原来的数据中比如包括了年龄，性别，身高等指标降维后的数据既然维度变小了，那么每一维都是什么含义呢？这个就很难解释了，所以PCA本质来说是无法解释降维后的数据的物理含义，换句话说就是降维完啦计算机能更好的认识这些数据，但是咱们就很难理解了。
• PCA对数据有两个假设：数据必须是连续数值型；数据中没有缺失值。
• 过拟合：PCA 保留了主要信息，但这个主要信息只是针对训练集的，而且这个主要信息未必是重要信息。有可能舍弃了一些看似无用的信息，但是这些看似无用的信息恰好是重要信息，只是在训练集上没有很大的表现，所以 PCA 也可能加剧了过拟合；

3. PCA的作用：

• 缓解维度灾难：PCA 算法通过舍去一部分信息之后能使得样本的采样密度增大（因为维数降低了），这是缓解维度灾难的重要手段；
• 降噪：当数据受到噪声影响时，最小特征值对应的特征向量往往与噪声有关，将它们舍弃能在一定程度上起到降噪的效果；
• 特征独立：PCA 不仅将数据压缩到低维，它也使得降维之后的数据各特征相互独立；

4. 方差的作用：咱们可以想象一下，如果一群人都堆叠在一起，我们想区分他们是不是比较困难，但是如果这群人站在马路两侧，我们就可以很清晰的判断出来应该这是两伙人。所以基于方差我们可以做的就是让方差来去判断咱们数据的拥挤程度，在这里我们认为方差大的应该辨识度更高一些，因为分的比较开（一条马路给隔开啦）。方差可以度量数值型数据的离散程度，数据若是想要区分开来，他那他们的离散程度就需要比较大，也就是方差比较大。

5. 协方差的作用：

6. 计算过程：(下图为采用特征值分解的计算过程，若采用SVM算法，则无需计算协方差矩阵！)

为什么我们需要协方差矩阵？我们最主要的目的是希望能把方差和协方差统一到一个矩阵里，方便后面的计算。

　　假设我们只有 a 和 b 两个变量，那么我们将它们按行组成矩阵 X：(与matlab不同的是，在numpy中每一列表示每个样本的数据，每一行表示一个变量。比如矩阵X，该矩阵表示的意义为：有m个样本点，每个样本点由两个变量组成！）

　　然后：

　　Cov(a,a) = E[(a-E(a))(a-E(a))], Cov(b,a) = E[(b-E(b))(a-E(a))]，因为E(b)=E(a)=0，所以大大简化了计算！！！(这就体现了去中心化的作用！)

　　我们可以看到这个矩阵对角线上的分别是两个变量的方差，而其它元素是 a 和 b 的协方差。两者被统一到了一个矩阵里。

7. 特征值与特征向量的计算方法-----特征值分解与奇异值分解法(SVD)(有关特征值与奇异值可见我的博文！)

(1) 特征值分解的求解过程较为简单，以下图为例子

(2) 特征值分解存在的缺点：

• 特征值分解中要求协方差矩阵A必须是方阵，即规模必须为n*n。
• 后期计算最小投影维度K时，计算量过大。
• 当样本维度很高时，协方差矩阵计算太慢；

(3) SVD算法(奇异值分解)的提出克服这些缺点，目前几乎所有封装好的PCA算法内部采用的都是SVD算法进行特征值、特征向量以及K值的求解。

• 奇异值(每个矩阵都有)：设A是一个mXn矩阵，称正半定矩阵A‘A的特征值的非负平方根为矩阵A的奇异值，其中A‘表示矩阵A的共扼转置矩阵(实数矩阵的共轭转置矩阵就是转置矩阵，复数矩阵的共轭转置矩阵就是上面所说的行列互换后每个元素取共轭)
• 只有方阵才有特征值。

(4) SVD算法的计算过程：(numpy中已经将SVD进行了封装，所以只需要调用即可)

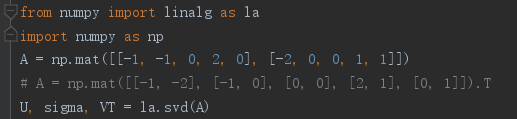
可以发现，采用SVD算法无需计算协方差矩阵，这样在数据量非常大的时候可以降低消耗。

• A为数据矩阵，大小为M*N(2*5)
• U是一个由与数据点之间具有最小投影误差的方向向量所构成的矩阵，大小为M*M(2*2),假如想要将数据由M维降至K维，只需要从矩阵U中选择前K个列向量，得到一个M*K的矩阵，记为Ureduce。按照下面的公式即可计算降维后的新数据：降维后的数据矩阵G = A.T * Ureduce.
• sigma为一个列向量，其包含的值为矩阵A的奇异值。
• VT是一个大小为N*N的矩阵，具体意义我们无需了解。

---

利用python实现PCA降维(采用SVD的方法)：

 from numpy import linalg as la
 import numpy as np
 #1.矩阵A每个变量的均值都为0，所以不用进行“去平均值”处理。倘若矩阵A的每个变量的均值不为0，则首先需要对数据进行预处理
 #  才可以进行协方差矩阵的求解。
 #2.与matlab不同的是，在numpy中每一列表示每个样本的数据，每一行表示一个变量。
 #  比如矩阵A，该矩阵表示的意义为：有5个样本点，每个样本点由两个变量组成！
 #3.np.mat()函数中矩阵的乘积可以使用 * 或 .dot()函数
 #  array()函数中矩阵的乘积只能使用 .dot()函数。而星号乘（*）则表示矩阵对应位置元素相乘，与numpy.multiply()函数结果相同。
 A = np.mat([[-1, -1, 0, 2, 0], [-2, 0, 0, 1, 1]])
 # A = np.mat([[-1, -2], [-1, 0], [0, 0], [2, 1], [0, 1]]).T
 U, sigma, VT = la.svd(A)
 print("U:")
 print(U)
 print("sigma:")
 print(sigma)
 print("VT:")
 print(VT)
 print("-"*30)
 print("降维前的数据：")
 print(A.T)
 print("降维后的数据:")
 print(A.T * U[:,0])

运行结果图：与上文采用特征值分解所得到的降维结果一致！

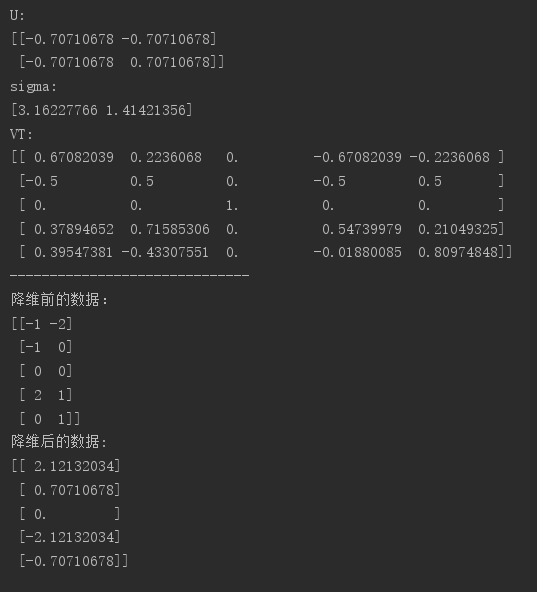
8.PCA的重建

众所周知，PCA可以将高维数据压缩为较少维度的数据，由于维度有所减少，所以PCA属于有损压缩，也就是，压缩后的数据没有保持原来数据的全部信息，根据压缩数据无法重建原本的高维数据，但是可以看作原本高维数据的一种近似。

还原的近似数据矩阵Q = 降维后的矩阵G * Ureduce.T

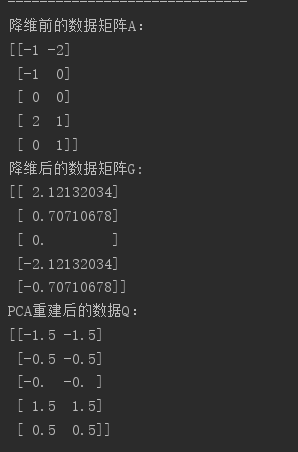
9.采用sklearn封装好的PCA实现数据降维(采用的是SVD算法)：

 import numpy as np
 from sklearn.decomposition import PCA
 # 利用sklearn进行PCA降维处理的时候，数据矩阵A的行数表示数据的个数，数据矩阵A的列数表示每条数据的维度。这与numpy中是相反的！
 # A = np.mat([[-1, -1, 0, 2, 0], [-2, 0, 0, 1, 1]]).T
 A = np.mat([[-1, -2], [-1, 0], [0, 0], [2, 1], [0, 1]])
 pca = PCA(n_components = 1)
 pca.fit(A)
 # 投影后的特征维度的方差比例
 print(pca.explained_variance_ratio_)
 # 投影后的特征维度的方差
 print(pca.explained_variance_)
 print(pca.transform(A))

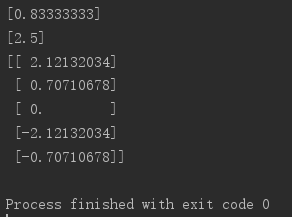
可以发现，采用sklearn封装的方法实现PCA与上文的方法达到的结果一致！

10.如何确定主成分数量(针对于Sklearn封装的PCA方法而言)

PCA算法将D维数据降至K维，显然K是需要选择的参数，表示要保持信息的主成分数量。我们希望能够找到一个K值，既能大幅降低维度，又能最大限度地保持原有数据内部的结构信息。实现的过程是通过SVD方法得到的S矩阵进行操作求解，

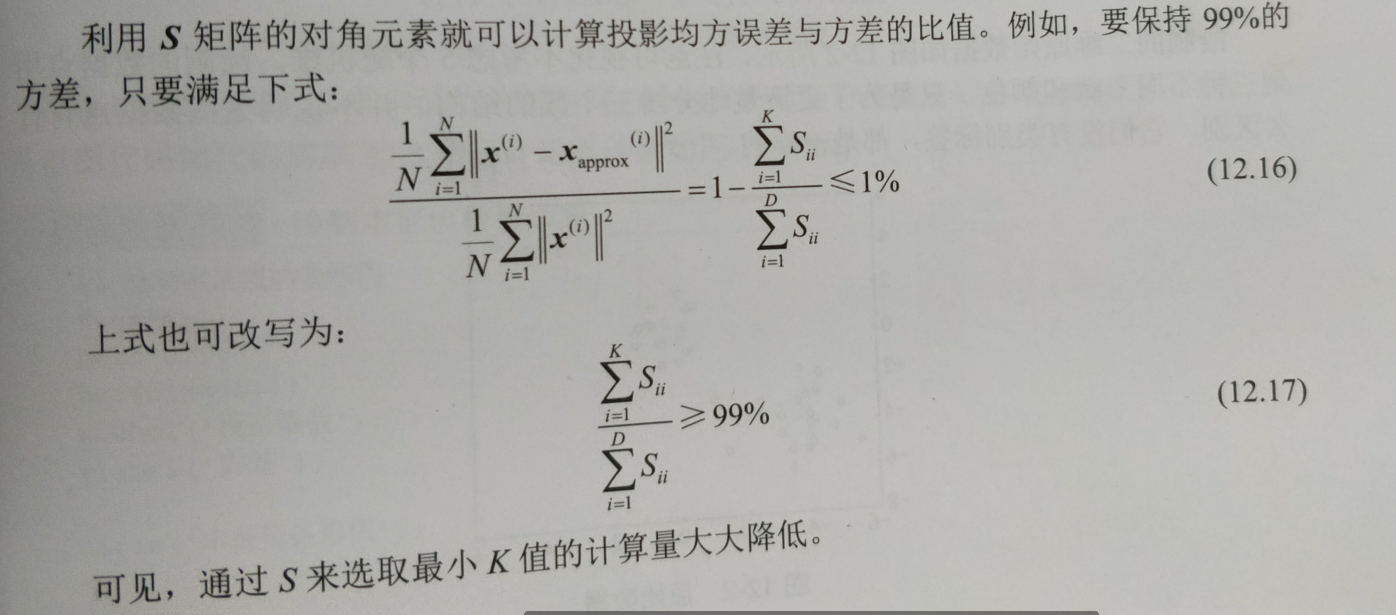
11.sklearn中封装的PCA方法的使用介绍。

PCA的函数原型

(1)主要参数介绍

n_components

• 这个参数类型有int型，float型，string型，默认为None。 它的作用是指定PCA降维后的特征数(也就是降维后的维度)。
• 若取默认(None)，则n_components==min(n_samples, n_features)，即降维后特征数取样本数和原有特征数之间较小的那个；
• 若n_components}设置为‘mle’并且svd_solver设置为‘full’则使用MLE算法根据特征的方差分布自动去选择一定数量的主成分特征来降维；
• 若0<n_components<1，则n_components的值为主成分方差的阈值； 通过设置该变量，即可调整主成分数量K。
• 若n_components≥1，则降维后的特征数为n_components；

copy

•  bool (default True)
• 在运行算法时，将原始训练数据复制一份。参数为bool型，默认是True，传给fit的原始训练数据X不会被覆盖；若为False，则传给fit后，原始训练数据X会被覆盖。

whiten

• bool, optional (default False)
• 是否对降维后的数据的每个特征进行归一化。参数为bool型，默认是False。

（2）主要方法介绍：

fit(X,y=None) ：用训练数据X训练模型，由于PCA是无监督降维，因此y=None。

transform(X,y=None) ：对X进行降维。

fit_transform(X) ：用训练数据X训练模型，并对X进行降维。相当于先用fit(X)，再用transform(X)。

inverse_transform(X) ：将降维后的数据转换成原始数据。(PCA的重建)

（3）主要属性介绍：

components：array, shape (n_components, n_features) ，降维后各主成分方向，并按照各主成分的方差值大小排序。

explained_variance：array, shape (n_components,) ，降维后各主成分的方差值，方差值越大，越主要。

explained_variance_ratio：array, shape (n_components,) ，降维后的各主成分的方差值占总方差值的比例，比例越大，则越主要。

singular_values：array, shape (n_components,) ，奇异值分解得到的前n_components个最大的奇异值。

二、LDA

1. 类间距离最大，类内距离最小(核心思想)

2. LDA的原理，公式推导见西瓜书，这里主要讲一下PCA与LDA的异同点！

• PCA为非监督降维，LDA为有监督降维PCA希望投影后的数据方差尽可能的大（最大可分性），因为其假设方差越多，则所包含的信息越多；而LDA则希望投影后相同类别的组内方差小，而组间方差大。LDA能合理运用标签信息，使得投影后的维度具有判别性，不同类别的数据尽可能的分开。举个简单的例子，在语音识别领域，如果单纯用PCA降维，则可能功能仅仅是过滤掉了噪声，还是无法很好的区别人声，但如果有标签识别，用LDA进行降维，则降维后的数据会使得每个人的声音都具有可分性，同样的原理也适用于脸部特征识别。
• 所以，可以归纳总结为有标签就尽可能的利用标签的数据（LDA），而对于纯粹的非监督任务，则还是得用PCA进行数据降维。
• LDA降维最低可以降维到（类别数-1），而PCA没有限制

参考资料：https://zhuanlan.zhihu.com/p/77151308?utm_source=qq&utm_medium=social&utm_oi=1095998405318430720