数据结构（十六）模式匹配算法--Brute Force算法和KMP算法

　　一、模式匹配

　　串的查找定位操作（也称为串的模式匹配操作）指的是在当前串（主串）中寻找子串（模式串）的过程。若在主串中找到了一个和模式串相同的子串，则查找成功；若在主串中找不到与模式串相同的子串，则查找失败。两种主要的模式匹配算法是Brute Force算法和KMP算法。

　　二、Brute Force算法

　　1.Brute Force算法也被称为朴素的模式匹配算法，是一种简单、直观的模式匹配算法。简单来说，就是对主串的每一个字符作为子串开头，与要匹配的字符串进行匹配。对主串做大循环，每个字符开头做次数为子串长度的小循环，直到匹配成功或全部遍历完成为止。

　　2.Brute Force算法的C语言代码实现：

/* 朴素的模式匹配法 */
int Index(String S, String T, int pos)
{
    int i = pos;    /* i用于主串S中当前位置下标值，若pos不为1，则从pos位置开始匹配 */
    int j = ;                /* j用于子串T中当前位置下标值 */
    while (i <= S[] && j <= T[]) /* 若i小于S的长度并且j小于T的长度时，循环继续 */
    {
        if (S[i] == T[j])     /* 两字母相等则继续 */
          {
            ++i;
             ++j;
          }
          else                 /* 指针后退重新开始匹配 */
          {
             i = i-j+;        /* i退回到上次匹配首位的下一位 */
             j = ;             /* j退回到子串T的首位 */
          }
    }
    if (j > T[])
        return i-T[];
    else
        return ;
}

　　3.Brute Force算法的Java语言代码实现：

    /*****************************朴素模式匹配算法*******************************************/
    public int indexOf_BF(StrMatchingINF str, int begin) throws Exception {
        if ((this != null) && (str != null) && (str.strLength() > 0 && (this.strLength() >= str.strLength()))) {
            int i = begin;
            int j = 0;
            int slen = this.strLength();          // strLength()函数返回的数组下标最大值
            int tlen = str.strLength();
            while ((i < slen) && (j < tlen)) {
                if (this.charAt(i) == str.charAt(j)) {
                    i++;
                    j++;
                } else {
                    i = i - j + 1;         // 注意：i退回到主串上次匹配首位的下一位
                    j = 0;                 // j回退到子串的首位
                }
            }
            if (j >= tlen) {    // 全部匹配成功
                return i - tlen;           // 返回 子串在主串中的下标
            } else {
                return 0;
            }
        } else {
            throw new Exception("主串为空或者子串为空或者子串长度大于主串长度");
        }
    }
 
    // BF算法比较次数统计
    public int indexOf_BFCount(StrMatchingINF str, int begin) throws Exception {
            int i = begin;
            int j = 0;
            int count = 0;
            int slen = this.strLength();
            int tlen = str.strLength();
            while ((i < slen) && (j < tlen)) {
                if (this.charAt(i) == str.charAt(j)) {
                    i++;
                    j++;
                } else {
                    i = i - j + 1;         // 注意：i退回到主串上次匹配首位的下一位
                    j = 0;                 // j回退到子串的首位
                }
                count ++;
            }
        return count;
    }
    /***********************************************************************************/

　　4.Brute Froce模式匹配算法简单且易于理解，但在一些情况下，时间效率非常低，其原因是主串s和模式串t中已有多个字符比较相等时，只要后面遇到一个字符比较不相等，就需要将主串的比较位置i回退。

　　假设主串的长度为n，子串的长度为m，则模式匹配的BF算法在最好情况下的时间复杂度为O(m),即主串的前m个字符刚好等于模式串的m个字符。

　　BF算法在最坏情况下的时间复杂度为O(m x n)：假设模式串的前m-1个字符串的相应字符序列比较总是相等，而模式串的第m个字符合主串的相应字符比较总是不相等时，此时，模式串的m个字符序列不许和主串相应字符序列一共比较n-m+1次，每次比较m个字符，总共需比较m x (n - m + 1)次，因此，其时间复杂度是O(m x n)。

　　例如1，主串s = “aaaab”，串长度n = 5，模式串t = “ab”，串长为m = 2。

　　每趟比较4次后匹配失败，i回到原位置加1，j返回到0，继续下一趟匹配，共计需要5 - 2 + 1 = 4趟，总共比较了4 x 2 = 8次。

　　例如2，主串s = “aaaaa”，串长度n = 5，模式串t = “ab”，串长为m = 2。

　　每趟比较4次后匹配失败，i回到原位置加1，j返回到0，继续下一趟匹配，共计需要5 - 2 + 1 = 4趟，这4趟是比较了4次，然而由于i继续加1，使得s的最后一位和t的第一位比较了一次，总共比较了4 x 2 + 1 = 9次。

　　三、KMP算法

　　1.KMP模式匹配算法也叫克努特-莫里斯-普拉特算法，可以大大避免重复遍历的情况。KMP算法的主要思想是，每当某趟匹配失败时，i指针不回退，而是利用已经得到的“部分匹配”的结果，将模式向右“滑动”尽可能远的一段距离后，继续进行比较。

　　2.在朴素的模式匹配算法中，主串的i值是不断地回溯来完成的，KMP算法就是为了避免没有必要的回溯发生。

　　3.既然i值不回溯，也就是不可以变小，那么要考虑的变化就是j值了，通过观察可以发现，j值的变化与主串没有关系，而是拒绝域T串的结构中是否有重复的问题，也就是说，j值的多少取决于当前字符之前的串的前后缀的相似度。

　　4.把T串各个位置的j值变化定义为一个数组next，那么next的长度就是T串的长度，于是，可以得到下面的函数定义：

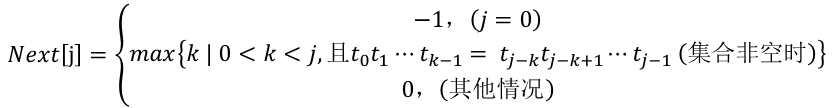
　　以模式串T = “abcabc”为例，
　　当j=0时，next[0]=-1;
　　当j=1时，next[1]=0;
　　当j=2时，等号左边最大为t0，      等号右边最大为t1，      由于t0不等于t1，所以next[2]=0;
　　当j=3时，等号左边最大为t0t1，    等号右边最大为t1t2，    由于t0不等于t2，所以next[3]=0;
　　当j=4时，等号左边最大为t0t1t2，  等号右边最大为t1t2t3，  由于t0等于t3，  所以next[4]=1;
　　当j=5时，等号左边最大为t0t1t2t3，等号右边最大为t1t2t3t4，由于t1等于t4,即有t0t1=t3t4，所以next[5]=next[4]+1=2;
 
　　以模式串T = “ababaaa”为例，
　　当j=0时，next[0]=-1;
　　当j=1时，子串为a，     next[1]=0;
　　当j=2时，子串为ab，    t0不等于t1，next[2]=0;
　　当j=3时，子串为aba，   t0=t2=‘a’，next[3]=1;
　　当j=4时，子串为abab，  t1=t3=‘b’，即有t0t1=t2t3，    则next[4]=next[3]+1=2;
　　当j=5时，子串为ababa， t2=t4=‘a’，即有t0t1t2=t2t3t4，则next[5]=next[4]+1=3;
　　当j=6时，子串为ababaa，t3不等于t5，则k=next[k]=next[3]=1；又因为t1不等于t5，则k=next[k]=next[1]=0；又因为t0等于t5，则next[6]=next[1]+1=1;

　　求解next[j]函数值的过程是一个递推过程：

　　初始时，next[0]=-1，next[1]=0;

　　若存在next[j]=k，则表明在模式串T中有“t0 t1... tk-1” = “tj-k tj-k+1 ... tj-1”　(0<k<j)，其中，k为满足等式的最大值。此时计算next[j+1]的值存在以下两种情况：

若tk = tj，则表明在模式串中存在“t0 t1... tk-1 tk” = “tj-k tj-k+1 ... tj-1 tj”　(0<k<j)并且不可能存在大于k的值满足上式，因此可以得到next[j+1]=next[j] + 1 = k + 1
若tk != tj，则表明在模式串中存在“t0 t1... tk-1 tk”不等于“tj-k tj-k+1 ... tj-1 tj”　(0<k<j)，此时可以把求next[j]的过程看成是一个模式匹配过程，整个模式串即是主串又是模式串。在当前匹配过程中，已有“t0 t1... tk-1” = “tj-k tj-k+1 ... tj-1”成立，则当tk不等于tj时，应将模式串T向右滑动值next[k]的位置，并把next[k]位置上的字符与主串中第j位置上的字符作比较。若此时next[k]的位置位置上的字符等于tj，则表明在“主串”T中第j+1个字符之前存在一个最大长度为next[k]的子串，使得t0~tnext[k] = tj-k~tj，因此有next[j+1]=next[k]+1。若此时此时next[k]的位置位置上的字符不等于tj，则将模式串T向右滑动继续匹配，直至某次比较有tk=tj，或某次比较有tk不等于tj且k=0，此时有next[j+1]=0

　　5.next[j]函数算法的Java语言代码实现

    private int[] get_Next(StrMatchingINF T) throws Exception {
        int[] next = new int[T.strLength()];
        int j = 1;
        int k = 0;
        next[0] = -1;
        next[1] = 0;
        while (j < T.strLength() - 1) {
            if (T.charAt(j) == T.charAt(k)) {
                next[j + 1] = k + 1;
                j++;
                k++;
            } else if (k == 0) {
                next[j + 1] = 0;
                j++;
            } else {
                k = next[k];
            }
        }
        return next;
    }

　　四、改进的KMP算法

　　1.以上定义的next[j]函数在某些情况下还存在缺陷。例如，主串s=“bbbcbbbbbc”，模式串t=“bbbbc”，在匹配时，当i=3，j=3时，s3不等于t3，则j向右滑动next[j]，接着还需要进行s3与t2，s3与t1，s3与t0的三次比较。实际上，因为模式串中的t0、t1、t2这三个字符与t3都相等，后三次比较结果与s3和t3的比较结果相同，因此，可以不必进行后三次的比较，而是直接将模式串向右滑动4个字符，比较s4与t0。

　　2.一般来说，若模式串t中存在tj=tk（k=next[j]）,且si不等于tj时，则下一次si不必与tk进行比较，而直接与t next[k]进行比较，因此，修正next[j]函数为nextval[j]：

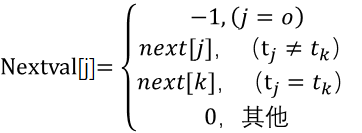
　　3.nextval[j]函数算法的Java语言代码实现

    private int[] get_NextVal(StrMatchingINF T) throws Exception {
        int[] nextval = new int[T.strLength()];
        int j = 1;
        int k = 0;
        nextval[0] = -1;
        while (j < T.strLength() - 1) {
            if (k == -1 || T.charAt(j) == T.charAt(k)) {
                j++;
                k++;
                if (T.charAt(j) != T.charAt(k)) {
                    nextval[j] = k;
                } else {
                    nextval[j] = nextval[k];
                }
            } else {
                k = nextval[k];
            }
        }
        return nextval;
    }

　　五、三种模式匹配算法的C语言代码实现（和Java实现有出入，数组下标为0的位置存储的是数组长度）：

#include "string.h"
#include "stdio.h"
#include "stdlib.h"
#include "io.h"
#include "math.h"
#include "time.h"
 
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 100 /* 存储空间初始分配量 */
 
typedef int Status;        /* Status是函数的类型,其值是函数结果状态代码，如OK等 */
typedef int ElemType;    /* ElemType类型根据实际情况而定，这里假设为int */
 
typedef char String[MAXSIZE+]; /*  0号单元存放串的长度 */
 
/* 生成一个其值等于chars的串T */
Status StrAssign(String T,char *chars)
{
    int i;
    if(strlen(chars)>MAXSIZE)
        return ERROR;
    else
    {
        T[]=strlen(chars);
        for(i=;i<=T[];i++)
            T[i]=*(chars+i-);
        return OK;
    }
}
 
Status ClearString(String S)
{
    S[]=;/*  令串长为零 */
    return OK;
}
 
/*  输出字符串T。 */
void StrPrint(String T)
{
    int i;
    for(i=;i<=T[];i++)
        printf("%c",T[i]);
    printf("\n");
}
 
/*  输出Next数组值。 */
void NextPrint(int next[],int length)
{
    int i;
    for(i=;i<=length;i++)
        printf("%d",next[i]);
    printf("\n");
}
 
/* 返回串的元素个数 */
int StrLength(String S)
{
    return S[];
}
 
/* 朴素的模式匹配法 */
int Index(String S, String T, int pos)
{
    int i = pos;            /* i用于主串S中当前位置下标值，若pos不为1，则从pos位置开始匹配 */
    int j = ;                /* j用于子串T中当前位置下标值 */
    while (i <= S[] && j <= T[]) /* 若i小于S的长度并且j小于T的长度时，循环继续 */
    {
        if (S[i] == T[j])     /* 两字母相等则继续 */
          {
            ++i;
             ++j;
          }
          else                 /* 指针后退重新开始匹配 */
          {
             i = i-j+;        /* i退回到上次匹配首位的下一位 */
             j = ;             /* j退回到子串T的首位 */
          }
    }
    if (j > T[])
        return i-T[];
    else
        return ;
}
 
/* 通过计算返回子串T的next数组。 */
void get_next(String T, int *next)
{
    int i,j;
      i=;
      j=;
      next[]=;
      while (i<T[])  /* 此处T[0]表示串T的长度 */
     {
        if(j== || T[i]== T[j])     /* T[i]表示后缀的单个字符，T[j]表示前缀的单个字符 */
        {
              ++i;
            ++j;
            next[i] = j;
        }
        else
            j= next[j];    /* 若字符不相同，则j值回溯 */
      }
}
 
/* 返回子串T在主串S中第pos个字符之后的位置。若不存在，则函数返回值为0。 */
/*  T非空，1≤pos≤StrLength(S)。 */
int Index_KMP(String S, String T, int pos)
{
    int i = pos;        /* i用于主串S中当前位置下标值，若pos不为1，则从pos位置开始匹配 */
    int j = ;            /* j用于子串T中当前位置下标值 */
    int next[];        /* 定义一next数组 */
    get_next(T, next);    /* 对串T作分析，得到next数组 */
    while (i <= S[] && j <= T[]) /* 若i小于S的长度并且j小于T的长度时，循环继续 */
    {
        if (j== || S[i] == T[j])     /* 两字母相等则继续，与朴素算法增加了j=0判断 */
          {
             ++i;
             ++j;
          }
          else             /* 指针后退重新开始匹配 */
               j = next[j];/* j退回合适的位置，i值不变 */
    }
    if (j > T[])
        return i-T[];
    else
        return ;
}
 
/* 求模式串T的next函数修正值并存入数组nextval */
void get_nextval(String T, int *nextval)
{
      int i,j;
      i=;
      j=;
      nextval[]=;
      while (i<T[])  /* 此处T[0]表示串T的长度 */
     {
        if(j== || T[i]== T[j])     /* T[i]表示后缀的单个字符，T[j]表示前缀的单个字符 */
        {
              ++i;
            ++j;
            if (T[i]!=T[j])      /* 若当前字符与前缀字符不同 */
                nextval[i] = j;    /* 则当前的j为nextval在i位置的值 */
              else
                nextval[i] = nextval[j];    /* 如果与前缀字符相同，则将前缀字符的 */
                                            /* nextval值赋值给nextval在i位置的值 */
        }
        else
            j= nextval[j];            /* 若字符不相同，则j值回溯 */
      }
}
 
int Index_KMP1(String S, String T, int pos)
{
    int i = pos;        /* i用于主串S中当前位置下标值，若pos不为1，则从pos位置开始匹配 */
    int j = ;            /* j用于子串T中当前位置下标值 */
    int next[];        /* 定义一next数组 */
    get_nextval(T, next);    /* 对串T作分析，得到next数组 */
    while (i <= S[] && j <= T[]) /* 若i小于S的长度并且j小于T的长度时，循环继续 */
    {
        if (j== || S[i] == T[j])     /* 两字母相等则继续，与朴素算法增加了j=0判断 */
          {
             ++i;
             ++j;
          }
          else             /* 指针后退重新开始匹配 */
               j = next[j];/* j退回合适的位置，i值不变 */
    }
    if (j > T[])
        return i-T[];
    else
        return ;
}
 
int main()
{
    int i,*p;
    String s1,s2;
 
    StrAssign(s1,"abcdex");
    printf("子串为: ");
    StrPrint(s1);
    i=StrLength(s1);
    p=(int*)malloc((i+)*sizeof(int));
    get_next(s1,p);
    printf("Next为: ");
    NextPrint(p,StrLength(s1));
    printf("\n");
 
    StrAssign(s1,"abcabx");
    printf("子串为: ");
    StrPrint(s1);
    i=StrLength(s1);
    p=(int*)malloc((i+)*sizeof(int));
    get_next(s1,p);
    printf("Next为: ");
    NextPrint(p,StrLength(s1));
    printf("\n");
 
    StrAssign(s1,"ababaaaba");
    printf("子串为: ");
    StrPrint(s1);
    i=StrLength(s1);
    p=(int*)malloc((i+)*sizeof(int));
    get_next(s1,p);
    printf("Next为: ");
    NextPrint(p,StrLength(s1));
    printf("\n");
 
    StrAssign(s1,"aaaaaaaab");
    printf("子串为: ");
    StrPrint(s1);
    i=StrLength(s1);
    p=(int*)malloc((i+)*sizeof(int));
    get_next(s1,p);
    printf("Next为: ");
    NextPrint(p,StrLength(s1));
    printf("\n");
 
    StrAssign(s1,"ababaaaba");
    printf("   子串为: ");
    StrPrint(s1);
    i=StrLength(s1);
    p=(int*)malloc((i+)*sizeof(int));
    get_next(s1,p);
    printf("   Next为: ");
    NextPrint(p,StrLength(s1));
    get_nextval(s1,p);
    printf("NextVal为: ");
    NextPrint(p,StrLength(s1));
    printf("\n");
 
    StrAssign(s1,"aaaaaaaab");
    printf("   子串为: ");
    StrPrint(s1);
    i=StrLength(s1);
    p=(int*)malloc((i+)*sizeof(int));
    get_next(s1,p);
    printf("   Next为: ");
    NextPrint(p,StrLength(s1));
    get_nextval(s1,p);
    printf("NextVal为: ");
    NextPrint(p,StrLength(s1));
 
    printf("\n");
 
    StrAssign(s1,"");
    printf("主串为: ");
    StrPrint(s1);
    StrAssign(s2,"");
    printf("子串为: ");
    StrPrint(s2);
    printf("\n");
    printf("主串和子串在第%d个字符处首次匹配（朴素模式匹配算法）\n",Index(s1,s2,));
    printf("主串和子串在第%d个字符处首次匹配（KMP算法） \n",Index_KMP(s1,s2,));
    printf("主串和子串在第%d个字符处首次匹配（KMP改良算法） \n",Index_KMP1(s1,s2,));
 
    return ;
}
 
输出为：
子串为: abcdex
Next为: 
 
子串为: abcabx
Next为: 
 
子串为: ababaaaba
Next为: 
 
子串为: aaaaaaaab
Next为: 
 
   子串为: ababaaaba
   Next为:
NextVal为: 
 
   子串为: aaaaaaaab
   Next为:
NextVal为: 
 
主串为:
子串为: 
 
主串和子串在第41个字符处首次匹配（朴素模式匹配算法）
主串和子串在第41个字符处首次匹配（KMP算法）
主串和子串在第41个字符处首次匹配（KMP改良算法）

　　六、三种模式匹配算法即其各自的比较次数统计算法的Java语言代码实现：

接口类：

package bigjun.iplab.stringMatching;
 
public interface StrMatchingINF {
 
    // 求顺序串的长度
    public int strLength();
    // 读取并返回串中的第index个字符值
    public char charAt(int index) throws Exception;
 
    // Brute-Force模式匹配算法
    public int indexOf_BF(StrMatchingINF str, int begin) throws Exception;
    // KMP模式匹配算法
    public int indexOf_KMP(StrMatchingINF str, int begin) throws Exception;
    // 改进的KMP模式匹配算法
    public int indexOf_ImprovedKMP(StrMatchingINF str, int begin) throws Exception;
 
}

实现类：

package bigjun.iplab.stringMatching;
 
public class StrMatching implements StrMatchingINF{
 
    private char[] strElem;
    private int curlength;
 
    // 构造方法：以字符串常量构造串对象
    public StrMatching(String str) {
        char[] tempCharArray = str.toCharArray();
        strElem = tempCharArray;
        curlength = tempCharArray.length;
    }
 
    public int strLength() {
        return curlength;
    }
 
    public char charAt(int index) throws Exception {
        if ((index < 0) || (index >= curlength)) {
            throw new Exception("索引值超出范围，无法给出对应字符");
        }
        return strElem[index];
    }
 
    /*****************************朴素模式匹配算法*******************************************/
    public int indexOf_BF(StrMatchingINF str, int begin) throws Exception {
        if ((this != null) && (str != null) && (str.strLength() > 0 && (this.strLength() >= str.strLength()))) {
            int i = begin;
            int j = 0;
            int slen = this.strLength();          // strLength()函数返回的数组下标最大值
            int tlen = str.strLength();
            while ((i < slen) && (j < tlen)) {
                if (this.charAt(i) == str.charAt(j)) {
                    i++;
                    j++;
                } else {
                    i = i - j + 1;         // 注意：i退回到主串上次匹配首位的下一位
                    j = 0;                 // j回退到子串的首位
                }
            }
            if (j >= tlen) {    // 全部匹配成功
                return i - tlen;           // 返回 子串在主串中的下标
            } else {
                return -1;
            }
        } else {
            throw new Exception("主串为空或者子串为空或者子串长度大于主串长度");
        }
    }
 
    // BF算法比较次数统计
    public int indexOf_BFCount(StrMatchingINF str, int begin) throws Exception {
            int i = begin;
            int j = 0;
            int count = 0;
            int slen = this.strLength();
            int tlen = str.strLength();
            while ((i < slen) && (j < tlen)) {
                if (this.charAt(i) == str.charAt(j)) {
                    i++;
                    j++;
                } else {
                    i = i - j + 1;         // 注意：i退回到主串上次匹配首位的下一位
                    j = 0;                 // j回退到子串的首位
                }
                count ++;
                if (j >= tlen)              // 全部匹配成功
                    return count;           // 返回 子串在主串中的下标
            }
        return count;
    }
 
    /************************************KMP模式匹配算法***********************************************/
    // KMP模式匹配算法
    public int indexOf_KMP(StrMatchingINF str, int begin) throws Exception {
        int[] next = get_Next(str);
        int i = begin;
        int j = 0;
        while (i < this.strLength() && j < str.strLength()) {
            if (j == -1 || this.charAt(i) == str.charAt(j)) {
                i++;
                j++;
            } else {
                j = next[j];
            }
        }
        if (j < str.strLength()) {
            return -1;
        } else {
            return (i - str.strLength());
        }
    }
 
    private int[] get_Next(StrMatchingINF T) throws Exception {
        int[] next = new int[T.strLength()];
        int j = 1;  // 注意这里，只给定了数组下标为0和1的初始值，所以要令j从1开始，和get_Nextval()区分开
        int k = 0;
        next[0] = -1;
        next[1] = 0;
        while (j < T.strLength() - 1) {
            if (T.charAt(j) == T.charAt(k)) {
                next[j + 1] = k + 1;
                j++;
                k++;
            } else if (k == 0) {
                next[j + 1] = 0;
                j++;
            } else {
                k = next[k];
            }
        }
        return next;
    }
 
    public int indexOf_KMPCount(StrMatchingINF str, int begin) throws Exception {
        int[] next = get_Next(str);
        int count = 0;
        int i = begin;
        int j = 0;
        while (i < this.strLength() && j < str.strLength()) {
            if (j == -1 || this.charAt(i) == str.charAt(j)) {
                i++;
                j++;
            } else if (j == 0) {
                i++;
            } else {
                j=next[j];
            }
            count++;
        }
        return count;
    }
 
    /*********************************改进的KMP模式匹配算法**********************************************/
    public int indexOf_ImprovedKMP(StrMatchingINF str, int begin) throws Exception {
        int[] next = get_NextVal(str);
        int i = begin;
        int j = 0;
        while (i < this.strLength() && j < str.strLength()) {
            if (j == -1 || this.charAt(i) == str.charAt(j)) {
                i++;
                j++;
            } else {
                j = next[j];
            }
        }
        if (j < str.strLength()) {
            return -1;
        } else {
            return (i - str.strLength());
        }
    }
 
    private int[] get_NextVal(StrMatchingINF T) throws Exception {
        int[] nextval = new int[T.strLength()];
        int j = 0;          // 注意这里，只给定了数组下标为0的初始值，所以要令j从0开始，和get_Next()区分开
        int k = -1;
        nextval[0] = -1;
        while (j < T.strLength() - 1) {
            if (k == -1 || T.charAt(j) == T.charAt(k)) {
                j++;
                k++;
                if (T.charAt(j) != T.charAt(k))
                    nextval[j] = k;
                else
                    nextval[j] = nextval[k];
 
            } else
                k = nextval[k];
 
        }
        return nextval;
    }
 
    public int indexOf_ImprovedKMPCount(StrMatchingINF str, int begin) throws Exception {
        int[] next = get_NextVal(str);
        int i = begin;
        int j = 0;
        int count = 0;
        while (i < this.strLength() && j < str.strLength()) {
            if (j == -1 || this.charAt(i) == str.charAt(j)) {
                i++;
                j++;
            } else if (j == 0) {
                i++;
            }{
                j = next[j];
            }
            count++;
        }
        return count;
    }
 
    /***********************************************************************/
 
    public static void main(String[] args) throws Exception {
        StrMatching str1 = new StrMatching("aaaaaaab");
        StrMatching str2 = new StrMatching("aaaab");
        System.out.println("采用BF算法，   主串和子串在主串数组下标为" + str1.indexOf_BF(str2, 0) + "的位置首次匹配成功");
        System.out.println("采用KMP算法，主串和子串在主串数组下标为" + str1.indexOf_KMP(str2, 0) + "的位置首次匹配成功");
        System.out.println("采用改进的KMP算法，主串和子串在主串数组下标为" + str1.indexOf_ImprovedKMP(str2, 0) + "的位置首次匹配成功");
        System.out.println("采用BF算法，   比较次数为: " + str1.indexOf_BFCount(str2, 0));
        System.out.println("采用KMP算法，比较次数为: " + str1.indexOf_KMPCount(str2, 0));
        System.out.println("采用改进的KMP算法，比较次数为: " + str1.indexOf_ImprovedKMPCount(str2, 0));
 
        System.out.println();    
 
        StrMatching str3 = new StrMatching("aaaaaaaa");
        StrMatching str4 = new StrMatching("aaaab");
        System.out.println("采用BF算法，   主串和子串在主串数组下标为" + str3.indexOf_BF(str4, 0) + "的位置首次匹配成功");
        System.out.println("采用KMP算法，主串和子串在主串数组下标为" + str3.indexOf_KMP(str4, 0) + "的位置首次匹配成功");
        System.out.println("采用改进的KMP算法，主串和子串在主串数组下标为" + str3.indexOf_ImprovedKMP(str4, 0) + "的位置首次匹配成功");
        System.out.println("采用BF算法，   比较次数为: " + str3.indexOf_BFCount(str4, 0));
        System.out.println("采用KMP算法，比较次数为: " + str3.indexOf_KMPCount(str4, 0));
        System.out.println("采用改进的KMP算法，比较次数为: " + str3.indexOf_ImprovedKMPCount(str4, 0));
 
        System.out.println();
 
        StrMatching str5 = new StrMatching("00000000000000000000000000000000000000000000000001");
        StrMatching str6 = new StrMatching("0000000001");
        System.out.println("采用BF算法，   主串和子串在主串数组下标为" + str5.indexOf_BF(str6, 0) + "的位置首次匹配成功");
        System.out.println("采用KMP算法，主串和子串在主串数组下标为" + str5.indexOf_KMP(str6, 0) + "的位置首次匹配成功");
        System.out.println("采用改进的KMP算法，主串和子串在主串数组下标为" + str5.indexOf_ImprovedKMP(str6, 0) + "的位置首次匹配成功");
        System.out.println("采用BF算法，   比较次数为: " + str5.indexOf_BFCount(str6, 0));
        System.out.println("采用KMP算法，比较次数为: " + str5.indexOf_KMPCount(str6, 0));
        System.out.println("采用改进的KMP算法，比较次数为: " + str5.indexOf_ImprovedKMPCount(str6, 0));
 
        System.out.println();
 
        StrMatching str7 = new StrMatching("bbbcbbbbc");
        StrMatching str8 = new StrMatching("bbbbc");
        System.out.println("采用BF算法，   主串和子串在主串数组下标为" + str7.indexOf_BF(str8, 0) + "的位置首次匹配成功");
        System.out.println("采用KMP算法，主串和子串在主串数组下标为" + str7.indexOf_KMP(str8, 0) + "的位置首次匹配成功");
        System.out.println("采用改进的KMP算法，主串和子串在主串数组下标为" + str7.indexOf_ImprovedKMP(str8, 0) + "的位置首次匹配成功");
        /* i从0到4，每一趟的次数为：4 , 3 , 2 , 1 , 5 */
        System.out.println("采用BF算法，   比较次数为: " + str7.indexOf_BFCount(str8, 0));
        /* next[j]    为-1、0、1、2、3 */
        /* i从0到4，每一趟的次数为：4 , 1 , 1 , 1 , 5 */
        System.out.println("采用KMP算法，比较次数为: " + str7.indexOf_KMPCount(str8, 0));
        /* nextval[j] 为-1、0、 0、0、3*/
        /* 由于t0、t1、t2都与t3相等，却s3不等于t3，所以s3不等于t0、t1、t2，所以没有必要让s3和t0、t1、t2比较*/
        /* i从0到4，每一趟的次数为：4 , 0 , 0 , 0 , 5 */
        System.out.println("采用改进的KMP算法，比较次数为: " + str7.indexOf_ImprovedKMPCount(str8, 0));
 
    }
 
}

输出：

采用BF算法，   主串和子串在主串数组下标为3的位置首次匹配成功
采用KMP算法，主串和子串在主串数组下标为3的位置首次匹配成功
采用改进的KMP算法，主串和子串在主串数组下标为3的位置首次匹配成功
采用BF算法，   比较次数为: 20
采用KMP算法，比较次数为: 11
采用改进的KMP算法，比较次数为: 8
 
采用BF算法，   主串和子串在主串数组下标为-1的位置首次匹配成功
采用KMP算法，主串和子串在主串数组下标为-1的位置首次匹配成功
采用改进的KMP算法，主串和子串在主串数组下标为-1的位置首次匹配成功
采用BF算法，   比较次数为: 24
采用KMP算法，比较次数为: 12
采用改进的KMP算法，比较次数为: 8
 
采用BF算法，   主串和子串在主串数组下标为40的位置首次匹配成功
采用KMP算法，主串和子串在主串数组下标为40的位置首次匹配成功
采用改进的KMP算法，主串和子串在主串数组下标为40的位置首次匹配成功
采用BF算法，   比较次数为: 410
采用KMP算法，比较次数为: 90
采用改进的KMP算法，比较次数为: 50
 
采用BF算法，   主串和子串在主串数组下标为4的位置首次匹配成功
采用KMP算法，主串和子串在主串数组下标为4的位置首次匹配成功
采用改进的KMP算法，主串和子串在主串数组下标为4的位置首次匹配成功
采用BF算法，   比较次数为: 15
采用KMP算法，比较次数为: 12
采用改进的KMP算法，比较次数为: 9

数据结构（十六）模式匹配算法--Brute Force算法和KMP算法的更多相关文章

串匹配模式中的BF算法和KMP算法
考研的专业课以及找工作的笔试题,对于串匹配模式都会有一定的考察,写这篇博客的目的在于进行知识的回顾与复习,方便遇见类似的题目不会纠结太多. 传统的BF算法传统算法讲的是串与串依次一对一的比较,举例设 ...
字符串匹配-BF算法和KMP算法
声明:图片及内容基于https://www.bilibili.com/video/av95949609 BF算法原理分析 Brute Force 暴力算法用来在主串中查找模式串是否存以及出现位置 ...
BF算法和KMP算法
这两天复习数据结构(严蔚敏版),记录第四章串中的两个重要算法,BF算法和KMP算法,博主主要学习Java,所以分析采用Java语言,后面会补上C语言的实现过程. 1.Brute-Force算法(暴力法 ...
【数据结构与算法】字符串匹配（Rabin-Karp 算法和KMP 算法）
Rabin-Karp 算法概念用于在一个字符串中查找另外一个字符串出现的位置. 与暴力法不同,基本原理就是比较字符串的哈希码 ( HashCode ) , 快速的确定子字符串是否等于被查 ...
字符串与模式匹配算法（三）：KMP算法
一.KMP算法介绍 KMP算法与前面的MP算法一脉相承,都是充分利用先前匹配的过程中已经得到的结果来避免频繁回溯.回顾一下MP算法,如下图的模式串偏移,当前模式字符串P的左端的p0与目标字符串T中tj ...
字符串匹配的BF算法和KMP算法学习
引言:关于字符串字符串(string):是由0或多个字符组成的有限序列.一般写作`s = "123456..."`.s这里是主串,其中的一部分就是子串. 其实,对于字符串大小关系 ...
串的模式匹配 BF算法和KMP算法
设有主串s和子串t,子串t的定位就是要在主串中找到一个与子串t相等的子串.通常把主串s称为目标串,把子串t称为模式串,因此定位也称为模式匹配. 模式匹配成功是指在目标串s中找到一个模式串t: 不成功则 ...
软件设计师_朴素模式匹配算法和KMP算法
1.从主字符串中匹配模式字符串(暴力匹配) 2. KMP算法
字符串匹配（BF算法和KMP算法及改进KMP算法）
#include <stdio.h> #include <string.h> #include <stdlib.h> #include<cstring> ...

随机推荐

Jib构建镜像的问题分析(Could not find or load main class ${start-class})
问题简述通过Jib插件将SpringBoot工程制作成Docker镜像成功,但是运行镜像的时候报错(Could not find or load main class ${start-class}) ...
基于Docker搭建大数据集群（二）基础组件配置
主要内容 jdk环境搭建 scala环境搭建 zookeeper部署 mysql部署前提 docker容器之间能免密钥登录 yum源更换为阿里源安装包微云分享 | tar包目录下 JDK 1.8 ...
Linux 部署vsftp服务及详解
一.FTP服务概述: FTP服务器(File Transfer Protocol Server)是在互联网上提供文件存储和访问服务的计算机,它们依照FTP协议提供服务. FTP(File Transf ...
ArchLinux安（重）装指南
说实话,我其实是不想要出这篇博客的.在我这一个月安装Arch的过程中,让我感触比较深的一点是: 没有谁比这个系统的官方更懂它. 尤其是这种比较复杂的系统,更是如此. 这几天,我经历了一次重装,系统坏了 ...
useradd、id、userdel、usermod、chsh、passwd、pwck
1.useradd [-cdefgGmkMsu] 用户名称用来添加用户 -c “备注“:加上备注文字 -d 路径:指定家目录 -e 有效期限:指定帐号的有效期限: -f 缓冲天数:指定在密码过期后多 ...
ElasticSearch实战系列三: ElasticSearch的JAVA API使用教程
前言在上一篇中介绍了ElasticSearch实战系列二: ElasticSearch的DSL语句使用教程---图文详解,本篇文章就来讲解下 ElasticSearch 6.x官方Java API的 ...
Scala 学习笔记之集合(3)
建立一个Java类,为了演示Java集合类型向Scala集合的转换: import java.util.ArrayList; import java.util.List; public class S ...
SpringBoot使用thymeleaf模板引擎引起的模板视图解析错误
Whitelabel Error Page This application has no explicit mapping for /error, so you are seeing this as ...
Asp.Net Core中Session使用
web程序中,Session是一个无法避开的点. 最近新开项目,打算从开始搭建一个基础的架子,后台用户登录成功后,需要保存session. 新建的asp.net core的模板已经包含了Session ...
Mac 10.14在新窗口中打开文件夹
Mac 10.14 Open folders in new window (high Sierra) System Preferences > Dock. Change "Prefer ...

数据结构（十六）模式匹配算法--Brute Force算法和KMP算法

数据结构（十六）模式匹配算法--Brute Force算法和KMP算法的更多相关文章

随机推荐

热门专题