python常用算法（5）——树，二叉树与AVL树

1，树

　　树是一种非常重要的非线性数据结构，直观的看，它是数据元素（在树中称为节点）按分支关系组织起来的结构，很像自然界中树那样。树结构在客观世界中广泛存在，如人类社会的族谱和各种社会组织机构都可用树形象表示。树在计算机领域中也得到了广泛应用，如在编译源程序时，可用树表示源程序的语法结构。又如在数据库系统中，树型结构也是信息的重要组织形式之一。一切具有层次关系的问题都可以用树来描述。

　　树（Tree）是元素的集合。树的定义是递归的，树是一种递归的数据结构。比如：目录结构。树是由n个结点组成的集合：如果n=0，那这就是一颗空树；如果 n>0，那么存在1个结点作为树的根节点，其他结点可以分为m个集合，每个集合本身又是一棵树。

• 1，树的根结点没有前驱结点，除根结点之外所有结点有且只有一个前驱结点。
• 2，树中所有结点可以有零个或者多个后继结点。

1.1  树的术语

1. 根节点：树的第一个节点，没有父节点的节点
2. 叶子节点：不带分叉的节点
3. 树的深度（高度）：就是分了多少层
4. 孩子节点，父节点：节点与节点之间的关系

　　如下图，我们分别解释：

　  1）B是K的祖先结点，K是B的子孙节点，E是K的双亲节点，K是E的孩子节点，K是L的兄弟节点。

　　2）树中一个结点的子节点个数为该节点的度，树中结点最大度数为树的度。

　　3）度大于0为节点结点，度等于0为叶子结点。

　　4）结点层次如图，结点深度时从根结点从顶往下累加，结点高度从低往上累加，树的高度（深度）是树的最大层数。

　　5）有序树：从左到右有次序，有关联。反之为无序树。

　　6）两结点之间的路径是两个结点之间所经过的结点序列构成的，路径长度是路径上所经过的边的个数。

　　7）森林是 m （m >=0）棵互不相交的集合。

　　上面观察实际上给了我们一种严格的定义树的方法：

• 1，树是元素的集合
• 2，该集合可以为空，这时树中没有元素，我们称树为空树（empty tree）
• 3，如果该集合不为空，那么该集合有一个根节点，以及0个或者多个子树。根节点与他的子树的根节点用一个边（edge）相连。

1.2  树的实现

　　树的示意图已经给出了树的一种内存实现方法：每个节点存储元素和多个指向子节点的指针。然而，子节点数目的是不确定的。一个父节点可能有大量的子节点，而另一个父节点可能只有一个子节点，而树的增删节点操作会让子节点的数目发生进一步的变换。这种不确定性就可能就可能带来大量的内存相关操作，并且容易造成内存的浪费。

　　一种经典的实现方法如下：

　　树的内存实现：拥有同一父节点的两个结点互为兄弟节点（sibling）。上图的实现方式中，每个节点包含一个指针指向第一个子节点，并且有另一个指针指向他的下一个兄弟节点。这样，我们就可以用统一的，确定的结构来表示每个节点。

1.3  树的实例——模拟文件系统

　　代码如下：

#_*_coding:utf-8_*_

class Node:
    def __init__(self, name, type='dir'):
        self.name = name
        self.type = type  # 'dir'  or ; 'file'
        self.children = []
        self.parent = None
        # 链式存储

    def __repr__(self):
        return self.name

class FileSystemTree:
    def __init__(self):
        self.root = Node("/")  # 首先我们创建一个根目录
        self.now = self.root

    def mkdir(self, name):
        # 创建一个文件目录，所以我们必须保证name是以 /结尾，如果没有，我们就加
        if name[-1] != '/':
            name += '/'
        node = Node(name)
        # 创建一个文件目录
        self.now.children.append(node)
        node.parent = self.now

    def ls(self):
        # 展示当前文件夹下的文件
        return self.now.children

    def cd(self, name):
        # 切换到指定目录  注意：支持绝对路径和相对路径
        # 相对路径是从now的路径下开始，而绝对路径是从root路径下开始找
        if name[-1] != '/':
            name += '/'
        if name == '../':
            self.now = self.now.parent
            return
        for child in self.now.children:
            if child.name == name:
                # 如果传入的目录名等于孩子的目录名，我们直接切换
                self.now = child
                return
        raise ValueError("invalid dir")

tree = FileSystemTree()
tree.mkdir('var/')
tree.mkdir('bin/')
tree.mkdir('usr/')
print(tree.ls())  # [var/, bin/, usr/]
tree.cd('bin/')
print(tree.ls())  # []
print(tree.root.children)  # [var/, bin/, usr/]

　　

2，二叉树

2.1  二叉树的定义

　　二叉树的链式存储：将二叉树的节点定义为一个对象，节点之间通过类似链表的链接方式来连接。

　　二叉树是一种特殊的树，它具有以下特点：

　　1）至多只有两棵子树，二叉树有左右之分，次序不能颠倒，也是递归形式定义。

　　2）或者为空二叉树，即 n=0

　　3）或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一颗二叉树。

　　4）每个节点至多有两个节点，即每个节点的度最多为2

　　5）二叉树中所有节点的形态有5种：空节点，无左右子树的节点，只有左子树的节点，只有右子树的节点和具有左右子树的节点

　　二叉树的定义如下：

class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None  # 左孩子
        self.rchild = None  # 右孩子

a = BiTreeNode("A")
b = BiTreeNode("B")
c = BiTreeNode("C")
d = BiTreeNode("D")
e = BiTreeNode("E")
f = BiTreeNode("F")
g = BiTreeNode("G")

e.lchild = a
e.rchild = g
a.rchild = c
c.lchild = b
c.rchild = d
g.rchild = f

root = e
print(root.lchild.rchild.data)
　　

　　二叉树的节点定义：

class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None  # 左孩子
        self.rchild = None  # 右孩子

　　

2.2  二叉树与度为2的有序树的区别：

　　1）度为2的树至少有3个结点，而二叉树可以为空。

　　2）左右次数。

2.3  二叉树的存储方式

　　二叉树的存储结构分为链式存储结构和顺序存储结构（列表）

二叉树的顺序存储方式

　　 思考：父节点和左孩子节点的编号下标有什么关系？

　　 0-1   1-3   2-5   3-7  4-9               i  ---->   2i+1

　　父节点和右孩子节点的编号下标有有什么关系？

　　0-2   1-4  2-6  3-8  4-10               i  ----->  2i+2

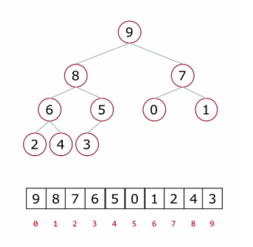
二叉树的链式存储

　　结构采用链式存储二叉树中的数据元素，用链建立二叉树中结点之间的关系。二叉树最常用的链式存储结构是二叉链，每个节点包含三个域，分别是数据元素域 data，左孩子链域 LChild 和 右孩子链域 rChild。与单链表带头结点和不带头节点的两种情况相似，二叉链存储结构的二叉树也有带头结点和不带头节点两种。

2.4   二叉树的遍历

　　那么如何遍历一颗二叉树呢？其实有两种通用的遍历树策略：

深度优先搜索（DFS）

　　在这个策略中，我们采用深度作为优先级，以便从根开始一直到达某个确定的叶子，然后再返回根到达另一个分支。

　　深度优先搜索策略又可以根据根节点，左孩子和右孩子的相对顺序被细分为先序遍历，中序遍历和后序遍历。

宽度优先搜索（BFS）

　　我们按照高度顺序一层一层的访问整棵树，高层次的节点将会被低层次的节点先被访问到。

下图中的顶点按照访问的顺序编号，按照1-2-3-4-5 的顺序来比较不同的策略：

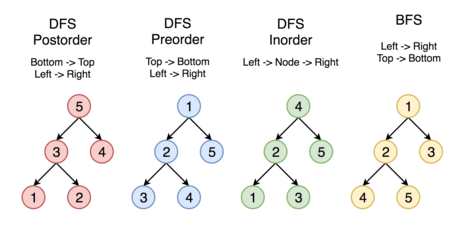
　　下面学习二叉树的遍历方式，以下图的二叉树为例，我们分别学习前序遍历，中序遍历，后序遍历，层次遍历。

前序遍历

　　思想：先访问根节点，再先序遍历左子树，然后再序遍历右子树。总的来说是 根——左——右

　　前序遍历如图所示：

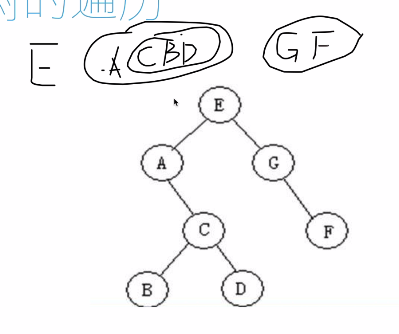
　　代码如下：

# 二叉树的前序遍历
def pre_order(root):
    if root:
        print(root.data)  # 先打印根节点
        pre_order(root.lchild)
        pre_order(root.rchild)

# pre_order(root)
'''
E
A
C
B
D
G
F
'''

中序遍历

　　思想：先中序访问左子树，再序访问根节点，最后中序遍历右子树。总的来说是 左——根——右

　　中序遍历如图所示：

　　代码如图所示：

# 中序遍历
def in_order(root):
    if root:
        in_order(root.lchild)
        print(root.data)
        in_order(root.rchild)

# in_order(root)
'''
A
B
C
D
E
G
F
'''

　　

后序遍历

　　思想：先后续访问左子树，然后后续访问右子树，最后访问根，总的来说是  左——右——根

　　后序遍历如图所示：

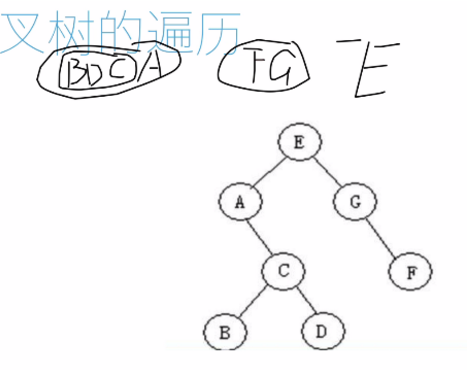
　　代码如下：

# 后序遍历
def post_order(root):
    if root:
        post_order(root.lchild)
        post_order(root.rchild)
        print(root.data)

post_order(root)
'''
B
D
C
A
F
G
E
'''

　　

层次遍历（宽度优先遍历）

　　思想：利用队列，依次将根，左子树，右子树存入队列，按照队列的先进先出规则来实现层次遍历。

　　按照上面的例子：

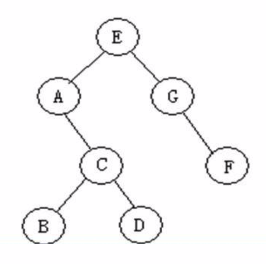
　　简单来说就是：根节点进队，然后出队，接着孩子节点入队，当队列为空则停止循环。

　　当E进队，然后E出队，E出队后，他的左孩子和右孩子进队，也就是AG；然后A出队，他没有左孩子，右孩子C进队，然后G出队，它没有左孩子，右孩子F进队。。。。。。

　　代码如下：

from collections import deque

def level_order(root):
    queue = deque()
    queue.append(root)
    while len(queue) > 0:  # 只要队不空
        node = queue.popleft()
        print(node.data)
        if node.lchild:
            queue.append(node.lchild)
        if node.rchild:
            queue.append(node.rchild)

level_order(root)
'''
E
A
G
C
F
B
D
'''

　　

3  几个特殊的二叉树

3.1  满二叉树

　　满二叉树作为一种特殊的二叉树，它是指：除了叶子节点，所有节点都有两个孩子（左子树和右子树），并且所有叶子节点深度都一样。

　　其特点有：

• 1）叶子节点只能出现在最下面一层
• 2）非叶子节点度一定是2
• 3）在同样深度的二叉树中，满二叉树的节点个数最多，节点个数为：2^h-1，其h为树的深度。

3.2  完全二叉树

　　完全二叉树是由满二叉树引申而来，假设二叉树深度为 h，那么除了第h层外，之前的每一层（1~h-1）的节点数都达到最大，即没有空的位置，而且第K层的子节点也都集中在左子树上（顺序）。

　　其具有以下特点：

• 1）叶子节点可以出现在最后一层或倒数第二层
• 2）最后一层的叶子节点一定集中在左部连续位置
• 3）完全二叉树严格按层序编号（可利用数组或列表实现，满二叉树同理）
• 4）若一个节点为叶子节点，那么编号比其大的节点均为叶子节点

3.3  二叉排序树

　　一颗二叉树或者空二叉树，如：左子树上所有关键字均小于根结点的关键字，右子树上的所有结点的关键字均大于根结点的关键字，左子树和右子树各是一颗二叉排序树。

3.4  平衡二叉树

　　树上任何一结点的左子树和右子树的深度只差不超过1 。

4， 二叉搜索树（BST）

4.1 二叉搜索树的定义

　　二叉搜索树(Binary Search Tree)，又名二叉排序树(Binary Sort Tree)。

　　由于二叉树的子节点数目确定，所以可以直接采用下图方式在内存中实现。每个节点有一个左子节点（left children）和右子节点（right children）。左子节点是左子树的根节点，右子节点是右子树的根节点。

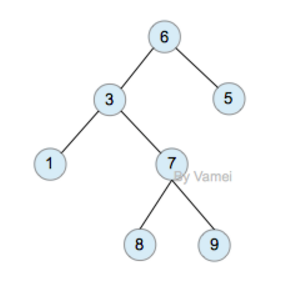
　　如果我们给二叉树加一个额外的条件，就可以得到一种被称为二叉搜索树（binary search tree）的特殊二叉树。二叉搜索树要求：每个节点都不比它左子树的任意元素小，而且不比它的右子树的任意元素大。

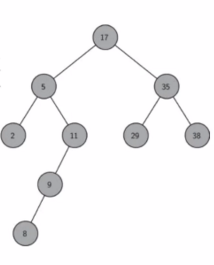
　　二叉搜索树是一颗二叉树且满足性质：设x是二叉树的一个节点。如果 y 是 x 左子树的一个节点，那么 y.key <= x.key；如果y 是x 的右子树的一个节点，那么 y.key >= x.key。

4.2  二叉搜索树的性质

• 1）若左子树不为空，则左子树上所有节点的值均小于或等于它的根节点的值
• 2）若右子树不为空，则右子树上所有节点的值均大于或等于它的跟节点的值
• 3）左右子树也分别为二叉搜索树

　　二叉搜索树，注意树中元素的大小。二叉搜索树可以方便的实现搜索算法。在搜索元素 x 的时候，我们可以将 x 和根节点比较：

• 1，如果 x 等于根节点，那么找到 x ,停止搜索（终止条件）
• 2，如果 x 小于根节点，那么搜索左子树
• 3，如果 x 大于根节点，那么搜索右子树

　　二叉搜索树所需要进行的操作次数最多与树的深度相等。n个结点的二叉搜索树的深度最多为 n ，最少为 log(n).

4.3  二叉搜索树的插入操作

　　从根节点开始，若插入的值比根节点的值小，则将其插入根节点的左子树；若比根节点的值大，则将其插入根节点的右子树。该操作可以使用递归进行实现。

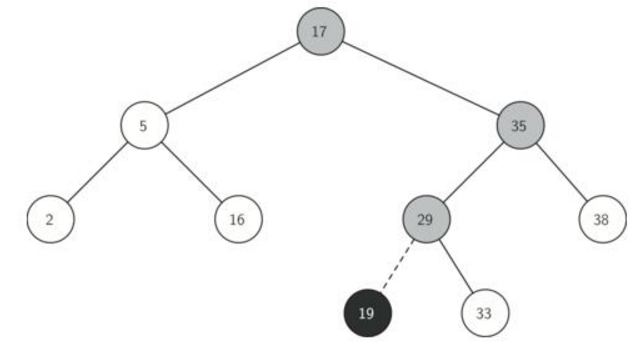
　　代码如下：

class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None  # 左孩子
        self.rchild = None  # 右孩子
        self.parent = None

class BST:
    def __init__(self, li=None):
        self.root = None
        if li:
            for val in li:
                self.insert_no_rec(val)

    def insert(self, node, val):
        if not node:
            node = BiTreeNode(val)
        elif val < node.data:
            node.lchild = self.insert(node.lchild, val)
            node.lchild.parent = node
        elif val > node.data:
            node.rchild = self.insert(node.rchild, val)
            node.rchild.parent = node
        return node

    def insert_no_rec(self, val):
        p = self.root
        if not p:  # 空树
            self.root = BiTreeNode(val)
            return
        while True:
            if val < p.data:
                if p.lchild:
                    p = p.lchild
                else:  # 左孩子不存在
                    p.lchild = BiTreeNode(val)
                    p.lchild.parent = p
                    return
            elif val > p.data:
                if p.rchild:
                    p = p.rchild
                else:
                    p.rchild = BiTreeNode(val)
                    p.rchild.parent = p
                    return
            else:
                return

4.4  二叉搜索树的查询操作

　　 从根节点开始查找，待查找的值是否与根节点的值相同，若相同则返回True；否则，判断待寻找的值是否比根节点的值小，若是则进入根节点左子树进行查找，否则进入右子树进行查找。该操作使用递归实现。

　　代码如下：

def query(self, node, val):
    if not node:
        return None
    if node.data < val:
        return self.query(node.rchild, val)
    elif node.data > val:
        return self.query(node.lchild, val)
    else:
        return node

4.5  二叉树的查询操作——找最大值（最小值）

　　查找最小值：从根节点开始，沿着左子树一直往下，直到找到最后一个左子树节点，按照定义可知，该节点一定是该二叉搜索树中的最小值节点。

　　程序代码如下：

def findMin(self, root):
    '''查找二叉搜索树中最小值点'''
    if root.left:
        return self.findMin(root.left)
    else:
        return root

　　查找最大值：从根节点开始，沿着右子树一直往下，知道找到最后一个右子树节点，按照定义可知，该节点一定是该二叉搜索树中的最大值节点。

　　程序代码如下：

def findMax(self, root):
    '''查找二叉搜索树中最大值点'''
    if root.right:
        return self.findMax(root.right)
    else:
        return root

4.6  二叉搜索树的删除操作

　　对二叉搜索树节点的删除操作分为以下三种情况

 　　1，如果要删除的节点是叶子节点：直接删除

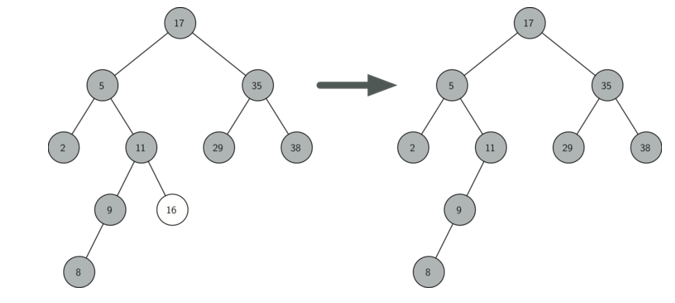
　　2，如果要删除的节点只有一个孩子：将此节点的父亲与孩子连接，然后删除该节点（注意：该待删节点可能只有左子树或者右子树）

　　3，如果要删除的节点有两个孩子：将其右子树的最小节点（该节点最多有一个右孩子）删除，并替换当前节点

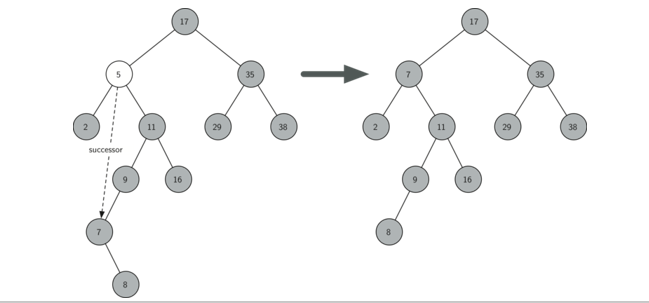
　　代码如下：

# _*_coding:utf-8_*_
import random

class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None  # 左孩子
        self.rchild = None  # 右孩子
        self.parent = None

class BST:
    def __init__(self, li=None):
        self.root = None
        if li:
            for val in li:
                self.insert_no_rec(val)

    def __remove_node_1(self, node):
        # 第一种情况：node是叶子节点
        if not node.parent:
            self.root = None
        if node == node.parent.lchild:  # node是他父亲的左孩子
            node.parent.lchild = None
            node.parent = None  # 可以不写
        else:  # node是他父亲的右孩子
            node.parent.rchild = None

    def __remove_node_21(self, node):
        # 情况2.1:node只有一个孩子，且为左孩子
        if not node.parent:  # 根节点
            self.root = node.lchild
            node.lchild.parent = None
        elif node == node.parent.lchild:  # node是它父亲的左孩子
            node.parent.lchild = node.lchild
            node.lchild.parent = node.parent
        else:  # node 是它父亲的右孩子
            node.parent.rchild = node.lchild
            node.lchild.parent = node.parent

    def __remove_node_22(self, node):
        # 情况2.2：node只有一个孩子，且为右孩子
        if not node.parent:
            self.root = node.rchild
        elif node == node.parent.lchild:
            node.parent.lchild = node.rchild
            node.rchild.parent = node.parent
        else:
            node.parent.rchild = node.rchild
            node.rchild.parent = node.parent

    def delete(self, val):
        if self.root:  # 不是空树
            node = self.query_no_rec(val)
            if not node:  # 不存在
                return False
            if not node.lchild and not node.rchild:  # 1，叶子节点
                self.__remove_node_1(node)
            elif not node.rchild:  # 2.1 只有一个左孩子
                self.__remove_node_21(node)
            elif not node.lchild:  # 2.2 只有一个右孩子
                self.__remove_node_22(node)
            else:
                # 3,两个孩纸都有
                min_node = node.rchild
                while min_node.lchild:  # 有左孩子
                    min_node = min_node.lchild
                node.data = min_node.data
                # 删除min_node
                if min_node.rchild:
                    self.__remove_node_22(min_node)
                else:
                    self.__remove_node_1(min_node)

　　

4.7  二叉搜索树的打印操作

　　实现二叉搜索树的前序遍历，中序遍历，后序遍历，并打印出来。其中中序遍历打印出来的数列是按照递增顺序排列。

　　程序的代码如下：

def printTree(self, root):
    # 打印二叉搜索树（中序打印，有序数列—）
    if root == None:
        return
    self.printTree(root.left)
    print(root.val, end=',')
    self.printTree(root.right)

4.8  二叉树的插入，查询，删除，打印完整代码

　　代码如下：

# _*_coding:utf-8_*_
import random

class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None  # 左孩子
        self.rchild = None  # 右孩子
        self.parent = None

class BST:
    def __init__(self, li=None):
        self.root = None
        if li:
            for val in li:
                self.insert_no_rec(val)

    def insert(self, node, val):
        if not node:
            node = BiTreeNode(val)
        elif val < node.data:
            node.lchild = self.insert(node.lchild, val)
            node.lchild.parent = node
        elif val > node.data:
            node.rchild = self.insert(node.rchild, val)
            node.rchild.parent = node
        return node

    def insert_no_rec(self, val):
        p = self.root
        if not p:  # 空树
            self.root = BiTreeNode(val)
            return
        while True:
            if val < p.data:
                if p.lchild:
                    p = p.lchild
                else:  # 左孩子不存在
                    p.lchild = BiTreeNode(val)
                    p.lchild.parent = p
                    return
            elif val > p.data:
                if p.rchild:
                    p = p.rchild
                else:
                    p.rchild = BiTreeNode(val)
                    p.rchild.parent = p
                    return
            else:
                return

    def query(self, node, val):
        if not node:
            return None
        if node.data < val:
            return self.query(node.rchild, val)
        elif node.data > val:
            return self.query(node.lchild, val)
        else:
            return node

    def query_no_rec(self, val):
        p = self.root
        while p:
            if p.data < val:
                p = p.rchild
            elif p.data > val:
                p = p.lchild
            else:
                return p
        return None

    def pre_order(self, root):
        if root:
            print(root.data, end=',')
            self.pre_order(root.lchild)
            self.pre_order(root.rchild)

    def in_order(self, root):
        if root:
            self.in_order(root.lchild)
            print(root.data, end=',')
            self.in_order(root.rchild)

    def post_order(self, root):
        if root:
            self.post_order(root.lchild)
            self.post_order(root.rchild)
            print(root.data, end=',')

    def __remove_node_1(self, node):
        # 第一种情况：node是叶子节点
        if not node.parent:
            self.root = None
        if node == node.parent.lchild:  # node是他父亲的左孩子
            node.parent.lchild = None
            node.parent = None  # 可以不写
        else:  # node是他父亲的右孩子
            node.parent.rchild = None

    def __remove_node_21(self, node):
        # 情况2.1:node只有一个孩子，且为左孩子
        if not node.parent:  # 根节点
            self.root = node.lchild
            node.lchild.parent = None
        elif node == node.parent.lchild:  # node是它父亲的左孩子
            node.parent.lchild = node.lchild
            node.lchild.parent = node.parent
        else:  # node 是它父亲的右孩子
            node.parent.rchild = node.lchild
            node.lchild.parent = node.parent

    def __remove_node_22(self, node):
        # 情况2.2：node只有一个孩子，且为右孩子
        if not node.parent:
            self.root = node.rchild
        elif node == node.parent.lchild:
            node.parent.lchild = node.rchild
            node.rchild.parent = node.parent
        else:
            node.parent.rchild = node.rchild
            node.rchild.parent = node.parent

    def delete(self, val):
        if self.root:  # 不是空树
            node = self.query_no_rec(val)
            if not node:  # 不存在
                return False
            if not node.lchild and not node.rchild:  # 1，叶子节点
                self.__remove_node_1(node)
            elif not node.rchild:  # 2.1 只有一个左孩子
                self.__remove_node_21(node)
            elif not node.lchild:  # 2.2 只有一个右孩子
                self.__remove_node_22(node)
            else:
                # 3,两个孩纸都有
                min_node = node.rchild
                while min_node.lchild:  # 有左孩子
                    min_node = min_node.lchild
                node.data = min_node.data
                # 删除min_node
                if min_node.rchild:
                    self.__remove_node_22(min_node)
                else:
                    self.__remove_node_1(min_node)

    def printTree(self, root):
        # 打印二叉搜索树（中序打印，有序数列—）
        if root == None:
            return
        self.printTree(root.left)
        print(root.val, end=',')
        self.printTree(root.right)

# 删除
tree = BST([1, 4, 2, 5, 3, 8, 6, 9, 7])
tree.in_order(tree.root)
print(" ")
tree.delete(4)
tree.delete(1)
tree.delete(8)
tree.in_order(tree.root)

'''
# 插入操作
tree = BST([4,6,7,9,2,1,3,5,8])
tree.pre_order(tree.root)
print(" ")
tree.in_order(tree.root)
print(" ")
tree.post_order(tree.root)
print(" ")
'''
4, 2, 1, 3, 6, 5, 7, 9, 8,
1, 2, 3, 4, 5, 6, 7, 8, 9,
1, 3, 2, 5, 8, 9, 7, 6, 4,
'''

# 查询操作
li = list(range(0, 500, 2))
random.shuffle(li)

tree = BST(li)
print(tree.query_no_rec(4).data)
# 4

'''

　　

4.9  二叉搜索树的效率

　　平均情况下，二叉搜索树进行搜索的时间复杂度为O(nlgn)

　　最坏情况下，二叉搜索树可能非常偏斜，如下图所示：

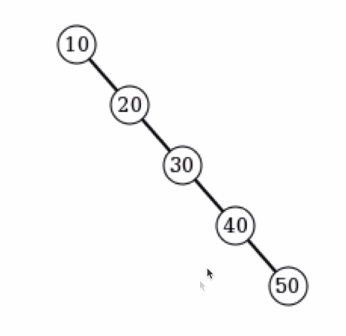
解决方案：

1. 随机化传入
2. AVL树

5，AVL树

5.1  AVL树的定义

　　在计算机科学中，AVL树（发明此树的三位科学家的名字首字母）是最早被发明的自平衡二叉查找树。在AVL树中，任一节点对应的两棵子树的最大高度为1，因此他也被称为高度平衡树。查找，插入和删除在平均和最坏的情况下的时间复杂度都是 O(log n)。增加和删除元素的操作则可能需要借由一次或多次树旋转，以实现树的重新平衡。

　　节点的平衡因子是它的左子树的高度减去它的右子树的高度（有时相反）。带有平衡因子1， 0或者-1的节点被认为是平衡的。带有平衡因子 -2 或 2的节点被认为是不平衡的，并需要重新平衡这个树，平衡因子可以直接存储在每个节点中，或从可能存储在节点的子树高度计算出来。

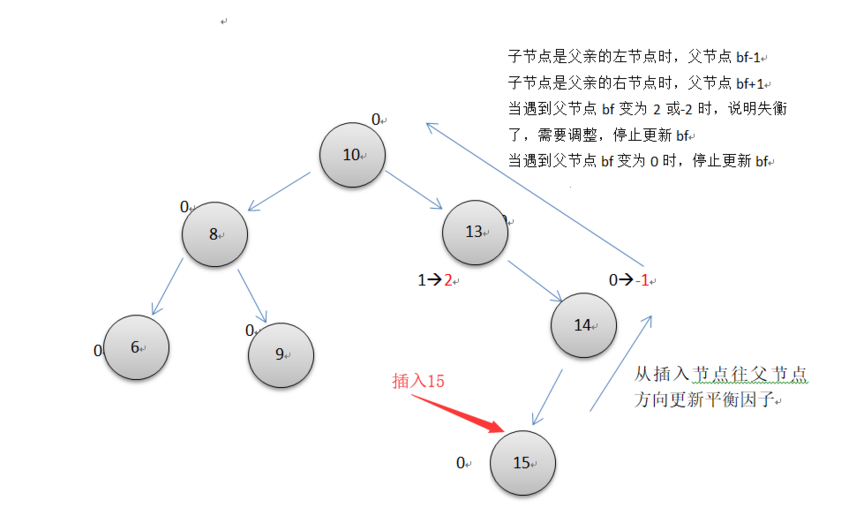
　　AVL树是一颗自平衡的二叉搜索树。一般要求每个节点的左子树和右子树的高度最多差1（空树的高度定义为 -1）。在高度为 h 的AVL树中，最少的节点数 S(h) = S(h-1) + S(h-2) + 1 得到，其中 S(0) = 1， S(1) = 2。

　　如下图所示，分别为高度为0， 1， 2， 3的AVL树所需要的最少节点数：

5.2  AVL树的性质

1. AVL树本质上还是一颗二叉搜索树
2. 根的左右子树的高度之差的绝对值（平衡因子）不能超过1
3. 根的左右子树都是平衡二叉树（二叉排序树，二叉搜索树）

5.3  AVL树的复杂度

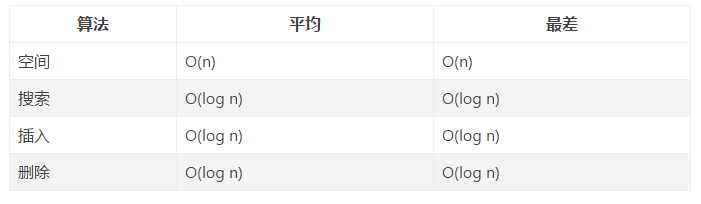
5.3  旋转

　　旋转是AVL树最重要的操作了，理解了旋转就理解了AVL树的实现原理。

左单旋转

　　下图节点上面的数字表示平衡因子

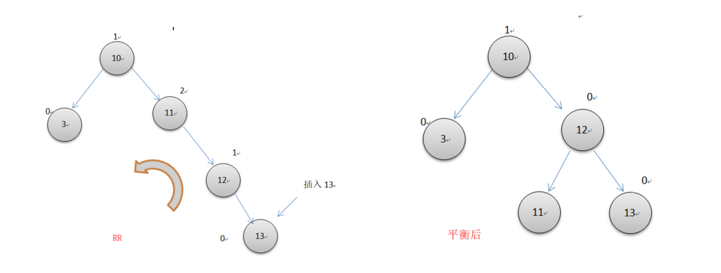
　　如上图所示，插入13后，右边子树11节点的平衡因子变为了2（左右节点的高度差），整个AVL树开始不平衡，这时便要开始以12为轴心进行一次左单旋转。具体旋转操作时原来11的父节点10指向12,12的左节点指向11，而11的右节点指向原来的12的左节点（此例中，12的左节点为空）。

右单旋转

　　上图中插入3后左子树不平衡了，根节点8的平衡因子变为了-2，此时应该以6为轴心向右单旋转一次，具体操作与左单旋转类似：8的左节点指向6的有节点（此时为7），6的右节点指向8，由于8原来是跟节点，没有父节点，所以根节点指向6.旋转后6和8节点都恢复0的平衡因子了。

左右双旋转

　　如上图所示，10节点的平衡因子是 -2，而它的左节点的平衡因子却为1，两个节点失去平衡的方向不一样，所以要先以7位轴心对节点6左单旋转一次，再以7为轴心对节点10右旋转一次。操作细节与上面单次循环一样。注意此时操作的3个结点的平衡因子要根据不同7的平衡因子单独调整。

右左双旋转

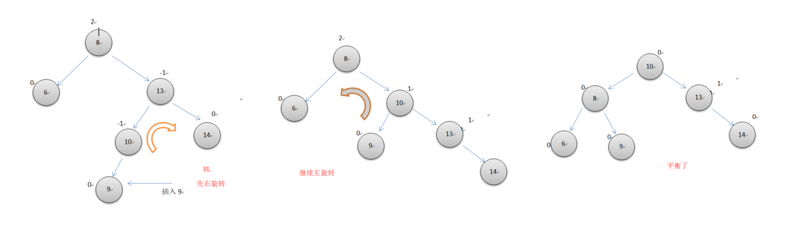
　　如上图所示，当一个节点的平衡因子为2，而它的右子节点的平衡因子为-1时，就需要先进行右旋转，再左旋转。注意中间节点13右旋转后的平衡因子变为1了。代码同左右双旋转类似。

5.4  AVL树——插入

　　插入一个节点可能会破坏 AVL树的平衡，可以通过旋转操作来进行修正。

　　插入一个节点后，只有从插入节点到根节点的路径上的节点的平衡可能被改变。我们需要找出第一个破坏了平衡条件的节点，称之为K，K的两棵子树的高度差2.

　　不平衡的出现可能有四种情况：

1，对K的左儿子的左子树进行一次插入

2，对K的左儿子的左子树进行一次插入

3，对K的右儿子的左子树进行一次插入

4，对K的右儿子的右子树进行一次插入

　　情况1和4是对称的，需要进行一次单旋转操作，情况2与3需要一次双旋转操作。

AVL插入——左旋

　　不平衡是由于对K的右孩子的右子树插入导致的：左旋

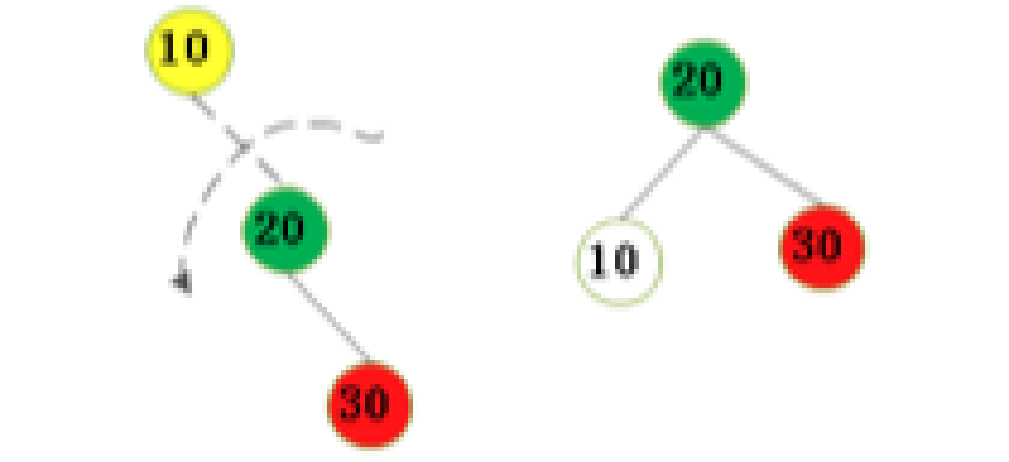
　　那代码过程如下图所示：

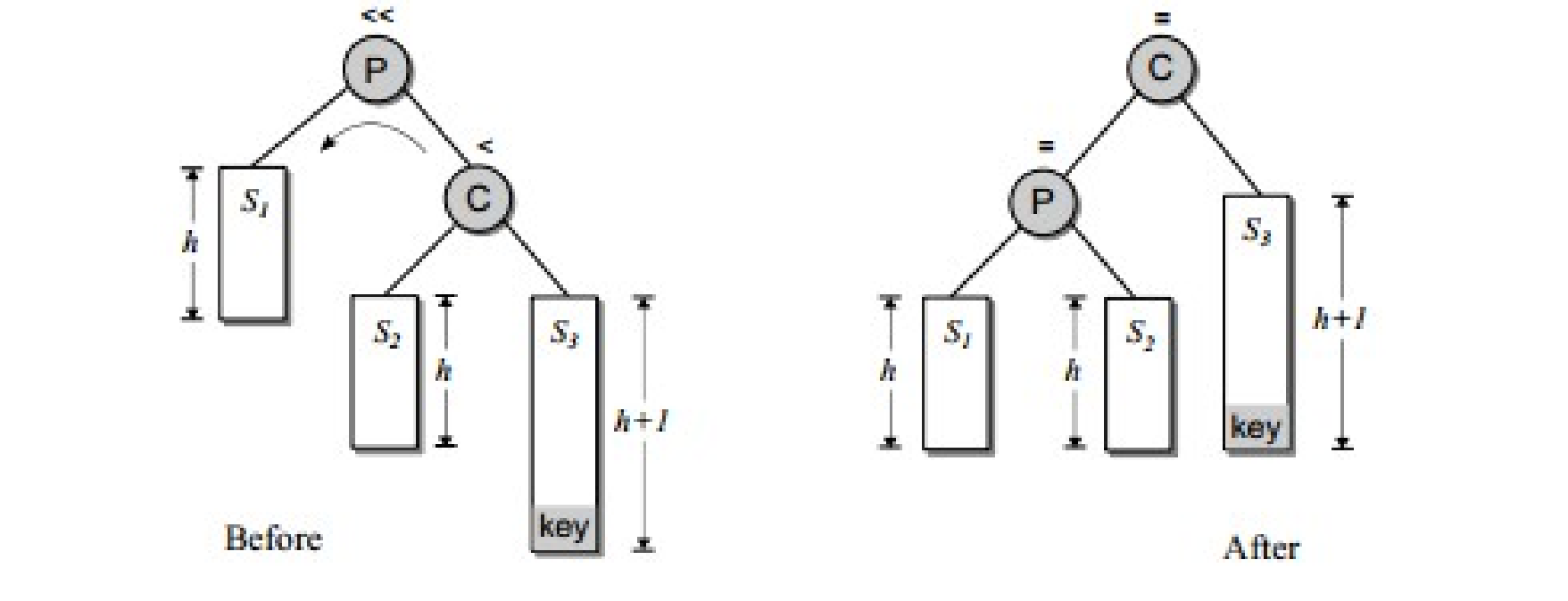
　　代码如下：

#_*_coding:utf-8_*_
from bst import BiTreeNode, BST

class AVLNode(BiTreeNode):
    def __init__(self, data):
        BiTreeNode.__init__(self, data)
        self.bf = 0

class AVLTree(BST):
    def __init__(self, li=None):
        BST.__init__(self, li)

    def rotate_left(self, p, c):
        s2 = c.lchild
        p.rchild = s2
        if s2:
            s2.parent = p
        c.lchild = p
        p.parent = c

        p.bf = 0
        c.bf = 0

AVL插入——右旋

　　不平衡是由于对K的左孩子的左子树插入导致的：右旋

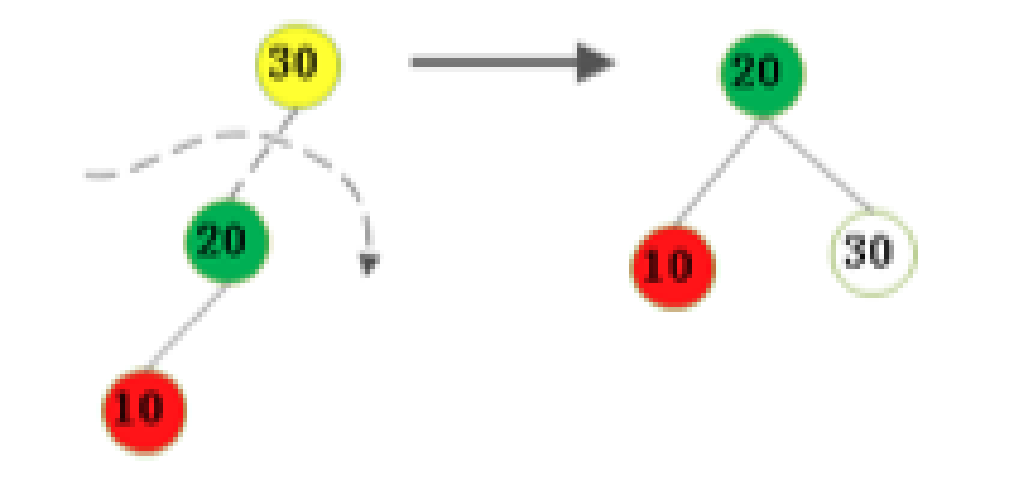
　　右旋插入的过程如下图：

　　代码如下：

#_*_coding:utf-8_*_
from bst import BiTreeNode, BST

class AVLNode(BiTreeNode):
    def __init__(self, data):
        BiTreeNode.__init__(self, data)
        self.bf = 0

class AVLTree(BST):
    def __init__(self, li=None):
        BST.__init__(self, li)

    def rotate_right(self, p, c):
        s2 = c.rchild
        p.lchild = s2
        if s2:
            s2.parent = p
        c.rchild = p
        p.parent = c

        p.bf = 0
        c.bf = 0

AVL插入——右旋-左旋

　　不平衡是由于对K的右孩子的左子树插入导致的：右旋-左旋

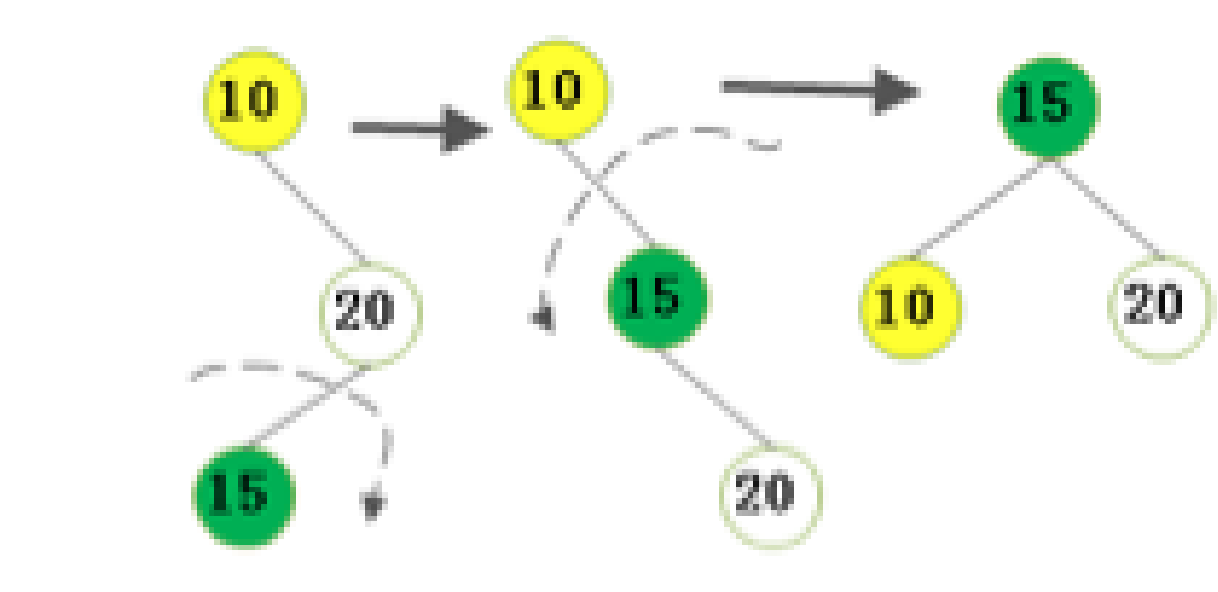
　　右旋左旋的代码流程如图所示：

　　代码如下：

#_*_coding:utf-8_*_
from bst import BiTreeNode, BST

class AVLNode(BiTreeNode):
    def __init__(self, data):
        BiTreeNode.__init__(self, data)
        self.bf = 0

class AVLTree(BST):
    def __init__(self, li=None):
        BST.__init__(self, li)

    def rotate_right_left(self, p, c):
        g = c.lchild

        s3 = g.rchild
        c.lchild = s3
        if s3:
            s3.parent = c
        g.rchild = c
        c.parent = g

        s2 = g.lchild
        p.rchild = s2
        if s2:
            s2.parent = p
        g.lchild = p
        p.parent = g

        # 更新bf
        if g.bf > 0:
            p.bf = -1
            c.bf = 0
        elif g.bf < 0:
            p.bf = 0
            c.bf = 1
        else :  # 插入的是g
            p.bf = 0
            c.bf = 0

AVL插入——左旋-右旋

　　还有一种不平衡是由于对K的左孩子的右子树插入导致的：左旋-右旋

　　代码的流程如下：

　　代码如下：

#_*_coding:utf-8_*_
from bst import BiTreeNode, BST

class AVLNode(BiTreeNode):
    def __init__(self, data):
        BiTreeNode.__init__(self, data)
        self.bf = 0

class AVLTree(BST):
    def __init__(self, li=None):
        BST.__init__(self, li)

    def rotate_left_right(self, p, c):
        g = c.rchild

        s2 = g.lchild
        c.rchild = s2
        if s2:
            s2.parent = c
        g.lchild = c
        c.parent = g

        s3 = g.rchild
        p.lchild = s3
        if s3:
            s3.parent = p
        g.rchild = p
        p.parent = g

        # 更新bf
        if g.bf < 0:
            p.bf = 1
            c.bf = 0
        elif g.bf > 0:
            p.bf = 0
            c.bf = -1
        else:
            p.bf = 0
            c.bf = 0

　　

AVL树的删除操作

　　删除操作比较复杂。

　　1，当前节点为要删除的节点且是树叶（无子树），直接删除，当前节点（为None）的平衡不受影响。

　　2.当前节点为要删除的节点且只有一个左儿子或右儿子，用左儿子或右儿子代替当前节点，当前节点的平衡不受影响。

　　3.当前节点为要删除的节点且有左子树右子树:如果右子树高度较高，则从右子树选取最小节点，将其值赋予当前节点，然后删除右子树的最小节点。如果左子树高度较高，则从左子树选取最大节点，将其值赋予当前节点，然后删除左子树的最大节点。这样操作当前节点的平衡不会被破坏。

　　4.当前节点不是要删除的节点，则对其左子树或者右子树进行递归操作。当前节点的平衡条件可能会被破坏，需要进行平衡操作。

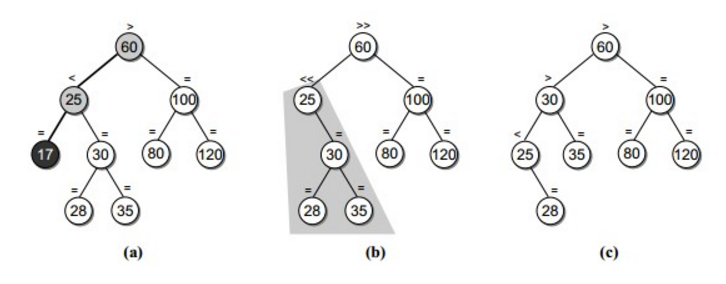
　　如上图，25为当前节点，左子树删除17后平衡条件被破坏，需要根据当前节点(25)的右子树(30)的左子树(28)高度是否高于右子树(35)的高度进行判断，若高于，进行双旋转，否则进行单旋转。

二叉搜索树的扩展应用——B树

　　B树（B-Tree）：B 树是一颗自平衡的多路搜索树，常用语数据库的索引。

1. 定义任意非叶子结点最多只有 M 个儿子；且 M>2 ；

2. 根结点的儿子数为 [2, M] ；

3. 除根结点以外的非叶子结点的儿子数为 [M/2, M] ；

4. 每个结点存放至少 M/2-1 （取上整）和至多 M-1 个关键字；（至少 2 个关键字）

5. 非叶子结点的关键字个数 = 指向儿子的指针个数 -1 ；

6. 非叶子结点的关键字： K[1], K[2], …, K[M-1] ；且 K[i] < K[i+1] ；

7. 非叶子结点的指针： P[1], P[2], …, P[M] ；其中 P[1] 指向关键字小于 K[1] 的子树， P[M] 指向关键字大于 K[M-1] 的子树，其它 P[i] 指向关键字属于 (K[i-1], K[i]) 的子树；

8. 所有叶子结点位于同一层；

如：（ M=3 ）

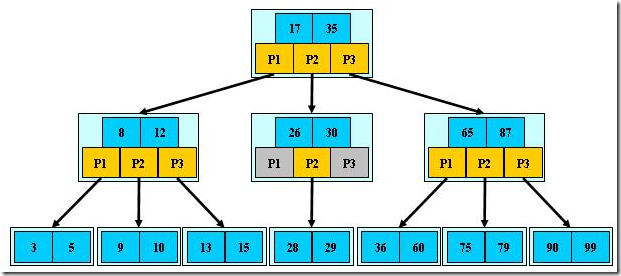
B- 树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为空，或已经是叶子结点；

B- 树的特性：

1. 关键字集合分布在整颗树中；

2. 任何一个关键字出现且只出现在一个结点中；

3. 搜索有可能在非叶子结点结束；

4. 其搜索性能等价于在关键字全集内做一次二分查找；

5. 自动层次控制；

由于限制了除根结点以外的非叶子结点，至少含有 M/2 个儿子，确保了结点的至少利用率，其最底搜索性能为：

　　

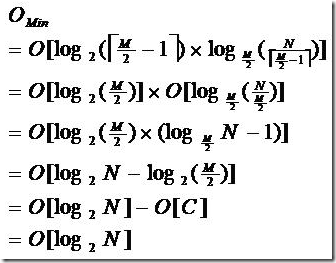
其中， M 为设定的非叶子结点最多子树个数， N 为关键字总数；

所以 B- 树的性能总是等价于二分查找（与 M 值无关），也就没有 B 树平衡的问题；

由于 M/2 的限制，在插入结点时，如果结点已满，需要将结点分裂为两个各占 M/2 的结点；删除结点时，需将两个不足 M/2 的兄弟结点合并；

二叉搜索树的扩展应用——B+ 树

B+ 树是 B- 树的变体，也是一种多路搜索树：

1. 其定义基本与 B- 树同，除了：

2. 非叶子结点的子树指针与关键字个数相同；

3. 非叶子结点的子树指针 P[i] ，指向关键字值属于 [K[i], K[i+1]) 的子树（ B- 树是开区间）；

5. 为所有叶子结点增加一个链指针；

6. 所有关键字都在叶子结点出现；

如：（ M=3 ）

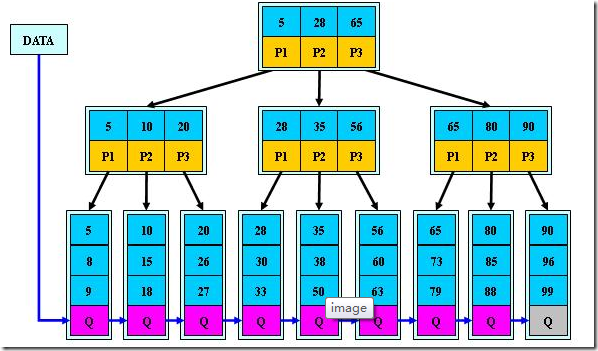
B+ 的搜索与 B- 树也基本相同，区别是 B+ 树只有达到叶子结点才命中（ B- 树可以在非叶子结点命中），其性能也等价于在关键字全集做一次二分查找；

B+ 的特性：

1. 所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；

2. 不可能在非叶子结点命中；

3. 非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；

4. 更适合文件索引系统；

二叉搜索树的扩展应用——B* 树

　　是B+ 树的变体，在B+ 树的非根和非叶子节点再增加指向兄弟的指针。

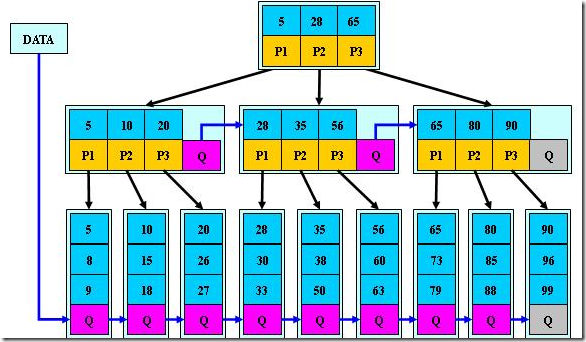
B* 树定义了非叶子结点关键字个数至少为 (2/3)*M ，即块的最低使用率为 2/3 （代替 B+ 树的 1/2 ）；

B+ 树的分裂：当一个结点满时，分配一个新的结点，并将原结点中 1/2 的数据复制到新结点，最后在父结点中增加新结点的指针； B+ 树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针；

B* 树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制 1/3 的数据到新结点，最后在父结点增加新结点的指针；

所以， B* 树分配新结点的概率比 B+ 树要低，空间使用率更高；

6，二叉树的图形化显示

6.1  在线生成 bst 树和 avl 树

　　学习过程中难免遇到理解的问题：图形化能很好的帮助我们理解问题，下面是两个在线生成二叉树的网址，根据自己需要看看，添加

• https://visualgo.net/zh/bst
• http://btv.melezinek.cz/binary-search-tree.html

6.2  程序自己生成二叉树

　　利用PyGraphviz模块画出二叉树

　　参考网址：http://pygraphviz.github.io/documentation/pygraphviz-1.5/  这里有详细的使用说明

安　　装该模块失败，参考这篇博客 https://blog.csdn.net/chirebingxue/article/details/50393755

　　使用了该模块以完成最后生成的二叉树显示，代码如下

import pygraphviz as pgv
    def draw(self, filename='./tree.png'):
        g = pgv.AGraph(strict=False, directed=True)
        g.node_attr['shape'] = 'circle'

        def traver(node):
            if node:
                if not node.parent:
                    g.add_node(node.key)
                else:
                    g.add_edge(node.parent.key, node.key)
                traver(node.left)
                traver(node.right)
        traver(self.root)
        g.layout('dot')
        g.draw(filename)

　　简单的测试改模块的效果

tree = AVLTree()
tree.insert(range(0, 20, 2))  # 自己简单实现了个可以接受一个可迭代对象的数值的插入
tree.draw()
tree.delete_key(14)
tree.draw('tree2.png')

　　最后生成下面的PNG图

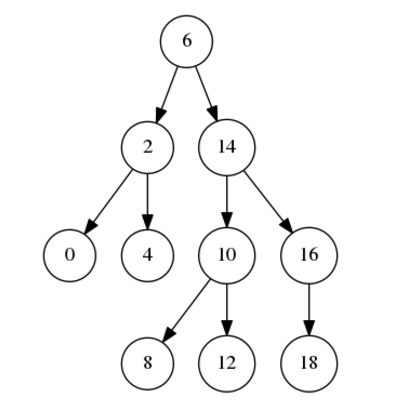
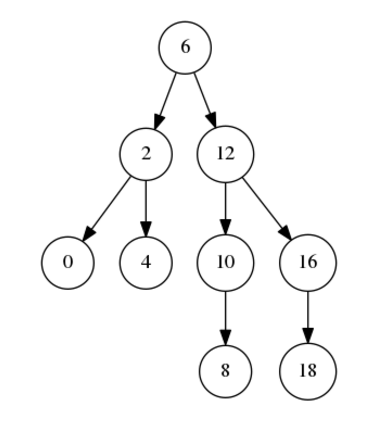
传送门：代码的GitHub地址：https://github.com/LeBron-Jian/BasicAlgorithmPractice

参考文献：树：https://www.cnblogs.com/hwnzy/p/11118942.html

二叉搜索树：https://www.cnblogs.com/lliuye/p/9118591.html

AVL树：https://www.cnblogs.com/yscl/p/10077607.html

B  B+  B* 树的学习笔记来自：https://www.nowcoder.com/test/question/done?tid=29244714&qid=14850#summary