AI/机器学习（计算机视觉/NLP）方向面试复习1

1. 判断满二叉树

所有节点的度要么为0，要么为2，且所有的叶子节点都在最后一层。

#include <iostream>
using namespace std;
class TreeNode {
public:
	int val;
	TreeNode* left;
	TreeNode* right;
//创建的时候输入参数x，会把x给val，nullptr给left和right
	TreeNode(int x) : val(x), left(nullptr), right(nullptr) {};
	TreeNode(int x, TreeNode* l, TreeNode* r) : val(x), left(l), right(r) {};
};
bool isfull(TreeNode* cur) {
	if (cur == nullptr) return true;
	if (cur->left == nullptr && cur->right != nullptr || cur->left != nullptr && cur->right == nullptr) return false;
	if (cur->left != nullptr) {
		isfull(cur->left);
		isfull(cur->right);
	}
	else {
		return true;
	}

}

int main() {
	int x = 1;
	TreeNode* left = new TreeNode(1);
	TreeNode* right = new TreeNode(1);
	TreeNode* root = new TreeNode(1, left, nullptr);
	cout << isfull(root) << endl;

}

重点在于创建一个TreeNode类，并且写出构造函数，调用构造函数创建节点。

2. 给定一个数，求该数的平方根，不用内置函数

二分法求解。递归。

float n;
float e = 0.001;
float findsquare(float left, float right) {
	float mid = (left + right) / 2;
	if (mid * mid - n >= 0 && mid * mid - n < e || mid * mid - n <= 0 && mid * mid - n >= -e) {
		return mid;
	}
	else {
		if (mid * mid > n) {
			findsquare(left, mid);
		}
		else {
			findsquare(mid, right);
		}
	}
}
int main() {
	cin >> n;
	cout<< findsquare(0, n)<<endl;

}

3. GAN model 内容

图像生成模型。图像生成模型比较了解的两种是GAN和diffusion。

GAN的基本流程：生成器可以用任何输出二维图片的网络，例如DNN或者CNN。

Discriminator一般输入为图片，输出为real或者fake。

每一轮，将reference输入到discriminator里判别为real，Generator输出的输入到discriminator里判别为假。

Generator的损失函数和Discriminator的损失函数都是二元交叉熵，也就是评估真实数据的概率，Generator的目标是最大化二元交叉熵，也就是让假结果都为正，而Discriminator是最小化二元交叉熵，让假结果都为假。

4. Diffusion model 内容

首先是数学知识：

条件概率公式

基于马尔科夫假设：当前概率仅与上一刻概率有关，与其他时刻无关。可以把条件概率其他项约掉。

高斯分布的KL散度公式：

参数重整化：整理出z作为网络输入，其他两个作为网络参数，可求梯度的。

多元VAE目标函数，都是根据x推理出z，用z预测x。多元VAE的z有多个。

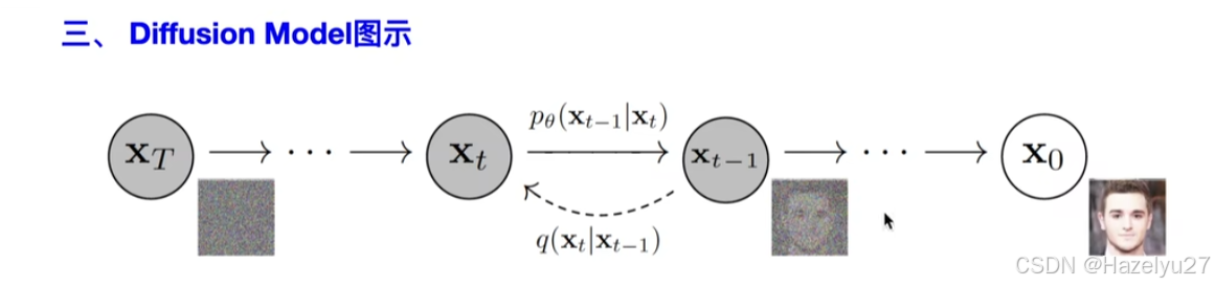
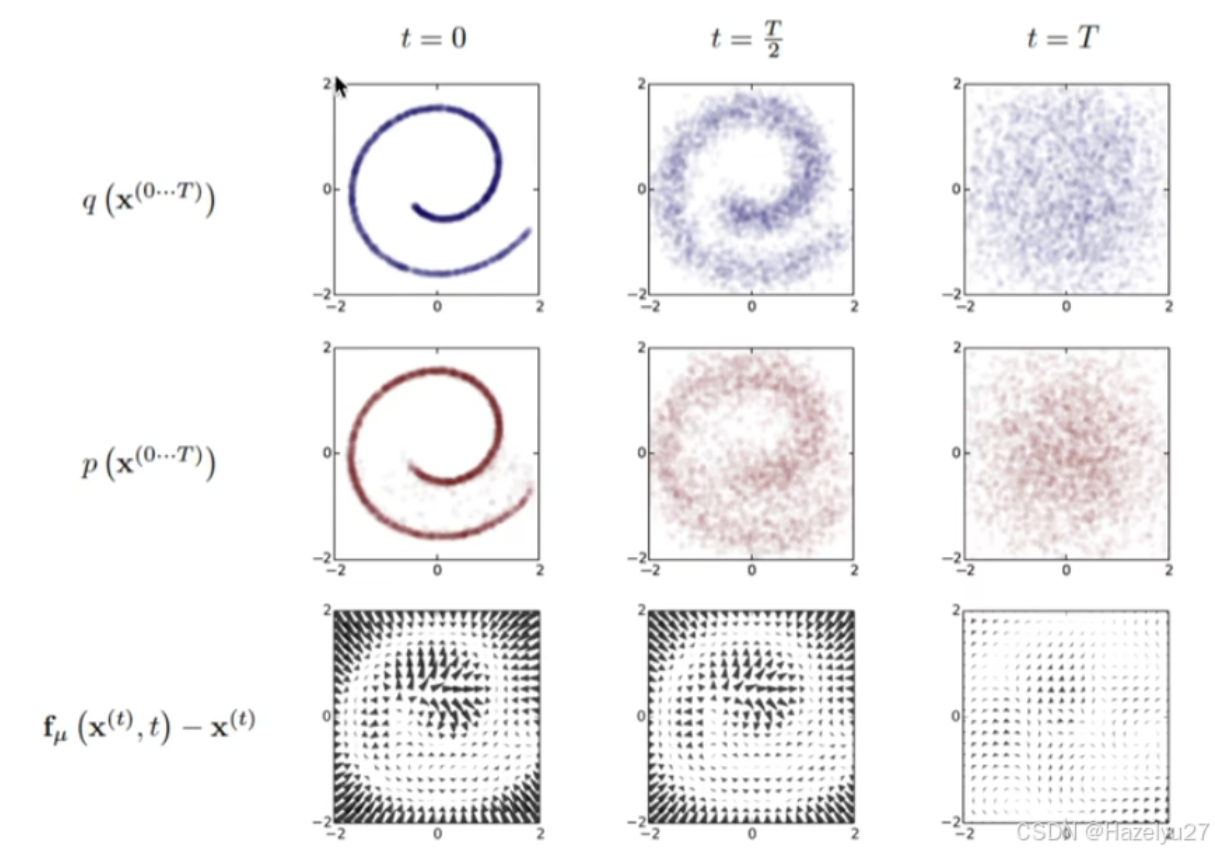
Diffusion Model 主要是两个过程，先从目标分布中扩散，得到噪声分布，是熵增的过程；

然后是从噪声分布中预测出目标分布。训练过程就是训练好这个x，这样就能在随机生成（例如高斯分布 ）的噪声中获得想要的目标分布。

扩散过程是p，逆扩散过程是q。漂移量是两者之间的差。

5. 二叉树的创建，插入和删除

这里应该是搜索二叉树，左节点小于自己，右节点大于自己。

删除先不写了不会

#include<iostream>
using namespace std;

class TreeNode {
public:
	int val;
	TreeNode* left;
	TreeNode* right;
	TreeNode(int x) :val(x), left(nullptr), right(nullptr) {};
	TreeNode(int x, TreeNode* l, TreeNode* r) : val(x), left(l), right(r) {};
};
TreeNode* insert(TreeNode* cur, int x) {
	if (cur == nullptr) {
		return new TreeNode(x);
	}
	if (x < cur->val) {
		cur->left = insert(cur->left, x);
	}
	else if (x > cur->val) {
		cur->right = insert(cur->right, x);
	}
	return cur;

}
//有点复杂，先不写了
TreeNode* deleteNode(TreeNode* cur, int val) {
	if (cur == nullptr) {
		return cur;
	}

}
int main() {
	int x = 1;
	TreeNode* root = new TreeNode(x);
	insert(root, 2);
}

6. Linux相关命令：

top 查看进程信息
df -h 查看硬盘使用情况
ps aux 查看所有进程
kill -9 pid 杀死编号为pid的进程
chmod 修改权限
grep 从文件名中找到包含某个字符串的数据
wc -l 统计行数
cut 分割一行内容
echo $PATH | cut -d ':' -f 3,5：输出PATH用:分割后第3、5列数据
find -name 查找文件
vim 浏览
head -3 显示前三行内容
docker:
docker ps -a 查看容器
docker attach 恢复容器
docker exec 挂起容器
docker run 跑容器
vim :n 到第n行 dd 删除当前行 :q！直接退出 :wq保存退出 gg=G格式化
ssh 登录服务器 scp -r传文件

7. 快速排序

#include <bits/stdc++.h>
using namespace std;
const int N = 100001;
void quicksort(int * arr, int l, int r){
    if(l >= r) return;
    int i = l-1, j = r+1;
    int mid = (l+r) / 2;
    int x = arr[mid];
    while(i<j){
        do i++; while(arr[i] < x) ;
       do j--; while(arr[j] > x) ;
       if(i<j) swap(arr[i],arr[j]);
    }
    quicksort(arr, l,j);
    quicksort(arr, j+1, r);

}
int main(){
    int n;
    cin>>n;
    int arr[N];
    for(int i =0;i<n;i++){
        cin>>arr[i];
    }
    quicksort(arr,0,n-1);
    for(int i =0;i<n;i++){
        cout<<arr[i]<<" ";
    }cout<<endl;
}

总是会忘记的点：先do后while，i和j初始化为l-1和r+1,因为进入dowhile循环后会自增or自减。

quicksort(arr, l,j); 这里不能用i代替j，因为i是一定大于x的，j是小于等于x的。要保证左边的段是小于等于x，右边的段是大于等于x。

8. xgboost和deepfm的性能。

（1）xgboost的结构：由多个回归决策树的模型构成。每一步都加入一个新的树。（前向分布算法，用贪心的策略）逐步优化基学习器。

优化第t棵树时，前面t-1颗树的参数是确定的。每轮的目标函数是n个样本的最小损失+正则项

正则项是前t颗树的复杂度。它由叶子结点的个数和每个节点值w的平方和决定，正则项是为了防止过拟合的。叶子节点越多，越容易过拟合。节点值大，就会导致这棵树占比比较多，也容易过拟合。

在机器学习中，一般通过梯度下降法优化参数。但是树模型是阶跃的，不连续的函数求不了梯度。所以xgboost是对每个叶节点求loss。 每个叶结点的loss可以用梯度来算，分别用了一阶导数和二阶导数也就是Hessian矩阵来找最优的分割点。

（2）xgboost如何用在推荐系统上？

将用户的上下文信息作为特征输入到xgboost中，预测用户的点击概率。所以xgboost是做回归的，放入到里面后

因为是回归任务，所以每轮迭代是选择叶节点的分裂点，然后根据分裂点得到一个值，这个值就是点击概率。多个数就是加权求平均。树的节点个数这些都是超参数。

（3）xgboost如何并行的？

并行时，在最优分裂点时用并行运算加快效率。它对特征进行分块，并行计算每个特征的增益，通过增益找到最佳分割点。再同步结果，选择最大的特征进行分割。

xgboost相对于梯度提升树（GBDT）有啥提升？

引入了二阶导数（Hessian），这在优化过程中比传统GBDT（只使用一阶导数信息）更为准确。

（4）Deepfm算法：

deep factorization machines 因子分解机。它对低阶特征做特征交互，另外一个DNN神经网络，做高阶特征交互。一般输出是两者的加权和。

因子分解机（FM）是什么？

FM是SVM的拓展，更适合用于处理稀疏特征。主要考虑到多维特征之间的交叉关系（就像SVM的核函数，用内积，但是却是用因子分解参数化的方式，而SVM中用的是稠密参数化的方式，这使得FM相比SVM的参数少了很多，更加容易计算）。其中参数的训练使用的矩阵分解的方法。

例如对于电影评分中的数据，用onehot向量建模，一个特征是非常稀疏的，非常长。因子分解机就是一种改进的二阶多项式模型，考虑到两个向量之间的相似性，例如喜欢这个类型电影的对另一个类型电影的喜欢。（推荐系统之FM（因子分解机）模型原理以及代码实践 - 简书）

本质上是用deepfm给召回阶段的候选集合排序。所以做的仅仅只是排序，不是召回。Loss用的是adam。

（5）为什么在大规模数据集上使用deepfm？

在处理用户行为数据和隐式反馈数据时，DeepFM通过其深度部分能够捕捉到复杂的非线性关系，表现较好。在大规模推荐系统中，如广告推荐、商品推荐等，DeepFM具有优势。

适合大规模数据和自动特征学习的场景，尤其在处理高维稀疏特征时表现出色。但需要大量数据和计算资源才能充分发挥其优势。

9. 判断链表里是否有环

可以用哈希法或者快慢指针法。快慢指针要注意：判断fast的next。不然会出界，并且初始化两个指针不能相同，不然当只有一个数据时返回就不对了。

    bool hasCycle(ListNode *head) {
        if (head == nullptr) return false;
        ListNode* slow = head;
        ListNode* fast = head->next;
        while(slow != fast){
            if(fast == nullptr || fast->next == nullptr) return false;
            slow = slow->next;
            fast = fast->next->next;
        }
        return true;
    }

哈希表法：注意插入是insert

bool hasCycle(ListNode *head) {
        unordered_set<ListNode*> sets;
        ListNode * cur = head;
        while(cur!=nullptr){
            if(sets.count(cur)) return true;
            sets.insert(cur);
            cur = cur->next;
        }
        return false;
    }

10. HDFS相关基础知识

对hadoop了解的不多，主要是使用了一些hadoop的命令进行数据读取。

HDFS是hadoop distribution file system。HDFS的文件分布在服务器集群上，提供副本和容错率保证。

适用于存储特别大的文件，采用流式数据进行访问。但不适合毫秒级别的访问，是有点延时的。

我是使用了一些命令行的命令，例如：

hadoop fs -copyFromLocal // copy file
hadoop fs mkdir
hadoop fs -ls