nim 3. 各种集合

其实我挺想先去学习一下nim的模块系统，毕竟我决定暂时放弃学习golang，就是因为感觉他的模块和包方面的设计，不像c#+nuget的组合那么舒服。

但是这里还是先学习一下集合吧，感觉这方面nim很有现代感。

常用的集合

• Arrays   定长数组
• Sequences  变长数组
• Tuples 元组

1）定长数组

定义Arrays数组的时候， 如果知道初始值，可以直接初始化。  如果不知道初始值，需要指定长度和类型。

var
  b = [5, 7, 9]    #有初始值
  d: array[7, string]  #无初始值
  c = []  # error      

定长数组的长度和类型都是定义的时候就要明确的。

2）变长数组

1 var
2   e1: seq[int] = @[]  #无初始值，需要指定类型
3   f = @["abc", "def"]  #有初始值，可以自动推断类型 ， 用 @ 符合，和定长数组区分。

这个有点像c#的List, 支持泛型的， 可以调用泛型方法初始化变长数组

var  e = newSeq[int]()

看看增删元素的代码：

1 var list = @[1,2]
2 list.add(3)
3 list.del(1)
4 echo list

这段代码输出：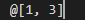

可以看到，del方法是按照下标删除元素。

切片

看代码

var list = @[1,2,3,4]
echo "切片:", list[1..2]

输出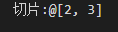：， 看来输出的还是变长数组。  再测试一下

var list = @[1,2,3,4]
var list2 = list[1..2]
list2.add(5)
echo "切片2: ", list2

输出：

感觉写起来和python没差别，却拥有了c的执行效率， 这应该就是nim的魅力所在吧。

感觉这篇有点长了， 元组就不多说了，感觉和c#的元组类型没啥差别。  【end】