笔记-AHOI2013 差异

AHOI2013 差异

---

方法1：SA

先板个后缀数组（带 \(height\) 不带 \(st\) 表），用单调队列递推每个后缀 \(sa_i\) 对答案的贡献，求和，用定值减之。

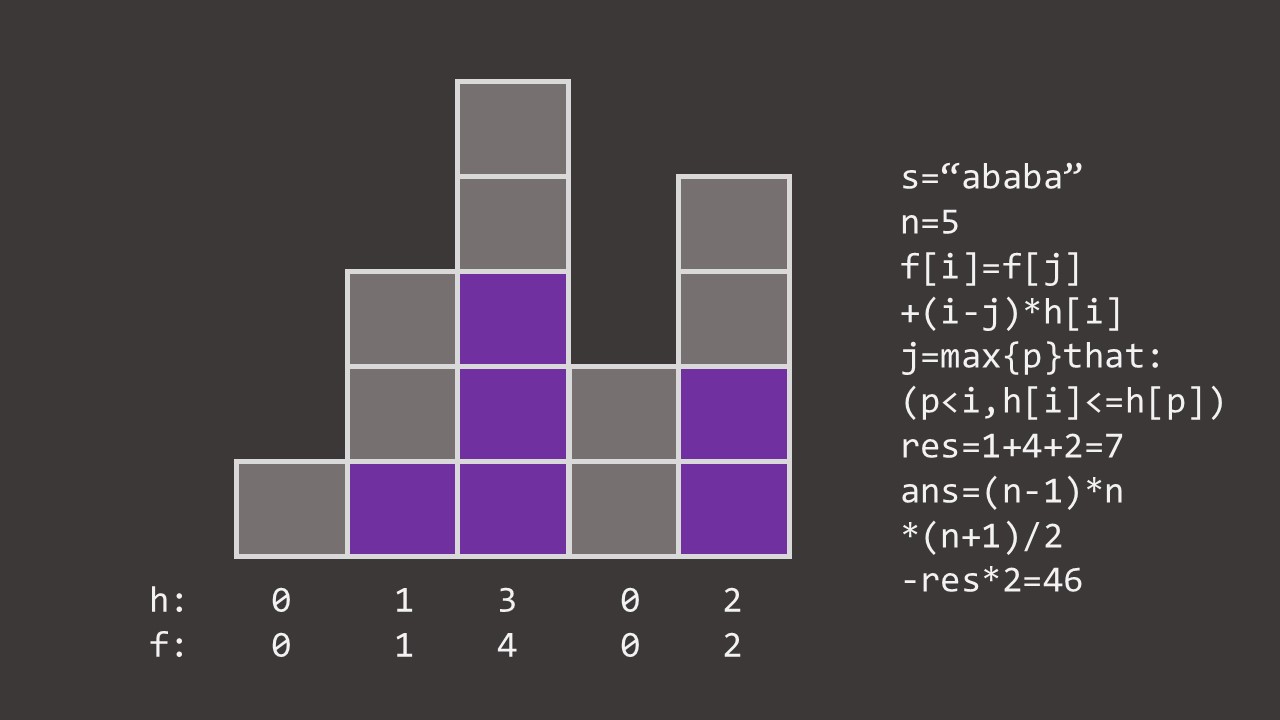
#include <bits/stdc++.h>
using namespace std;

//Start
typedef long long ll;
typedef double db;
#define mp(a,b) make_pair(a,b)
#define x first
#define y second
#define b(a) a.begin()
#define e(a) a.end()
#define sz(a) int((a).size())
#define pb(a) push_back(a)
const int inf=0x3f3f3f3f;
const ll INF=0x3f3f3f3f3f3f3f3f;

//Data
const int N=5e5;
int n;
char s[N+7];

//SuffixArray
int m,c[N+7],tp[N+7],rk[N+7],sa[N+7],h[N+7];
void csort(){
	for(int i=0;i<=m;i++) c[i]=0;
	for(int i=1;i<=n;i++) c[rk[i]]++;
	for(int i=1;i<=m;i++) c[i]+=c[i-1];
	for(int i=n;i>=1;i--) sa[c[rk[tp[i]]]--]=tp[i];
}
void build(){
	for(int i=1;i<=n;i++) rk[i]=s[i],tp[i]=i;
	m=128,csort();
	for(int w=1,p=1,i;p<n;w<<=1,m=p){
		for(p=0,i=n-w+1;i<=n;i++) tp[++p]=i;
		for(i=1;i<=n;i++)if(sa[i]>w) tp[++p]=sa[i]-w;
		csort(),swap(rk,tp),rk[sa[1]]=p=1;
		for(i=2;i<=n;rk[sa[i]]=p,i++)
			if(tp[sa[i]]!=tp[sa[i-1]]||tp[sa[i]+w]!=tp[sa[i-1]+w]) p++;
	}
	for(int i=1,j,k=0;i<=n;h[rk[i++]]=k)
		for(k=k?k-1:k,j=sa[rk[i]-1];s[i+k]==s[j+k];k++);
}

//Main
int main(){
	scanf("%s",&s[1]);
	n=strlen(&s[1]),build();
	vector<int> q(n+7); int lst=0,qc=0;
	vector<ll> f(n+7); ll res=0;
	for(int i=1;i<=n;i++){
		while(qc&&h[q[qc]]>h[i]) qc--;
		int j=qc?q[qc]:lst;
		res+=(f[i]=f[j]+1ll*(i-j)*h[i]);
		if(!h[i]) lst=i;
		else q[++qc]=i;
	}
	for(int i=1;i<=n;i++)
		printf("%d ",sa[i]);puts("");
	for(int i=1;i<=n;i++)
		printf("%d ",h[i]);puts("");
	for(int i=1;i<=n;i++)
		printf("%lld ",f[i]);puts("");
	printf("%lld\n",1ll*(n-1)*n*(n+1)/2-res*2);
	return 0;
}

---

方法2：SAM

注意到这个式子是 \(\tt SAM\) \(\bf parent~tree\) 树上两点的距离，计算每条边的贡献和即可。

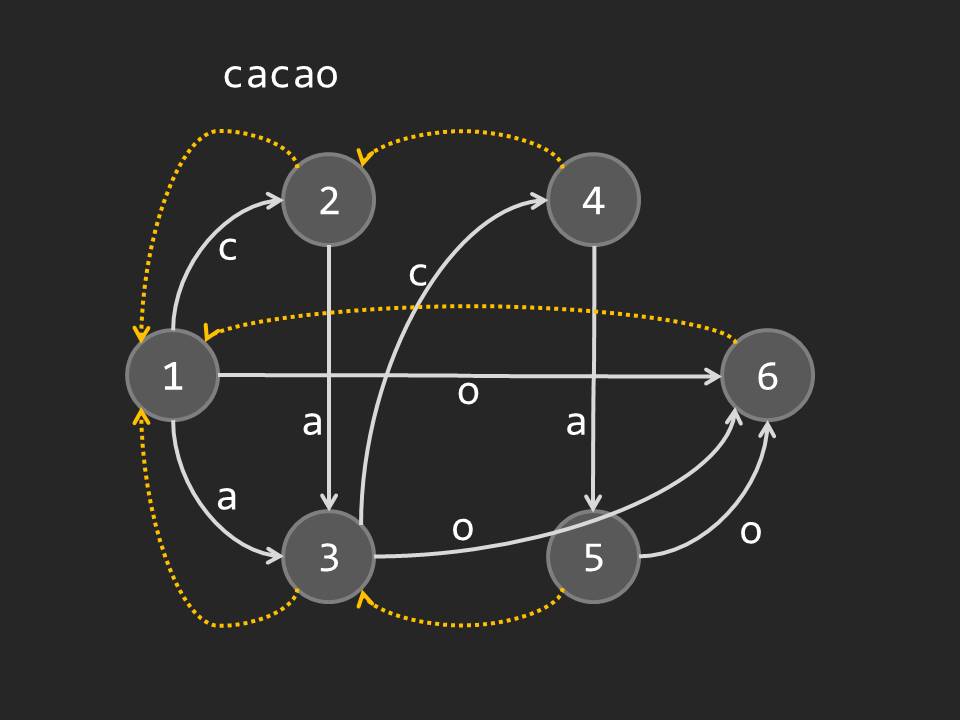
#include <bits/stdc++.h>
using namespace std;

//Start
typedef long long ll;
typedef double db;
#define mp(a,b) make_pair(a,b)
#define x first
#define y second
#define b(a) a.begin()
#define e(a) a.end()
#define sz(a) int((a).size())
#define pb(a) push_back(a)
const int inf=0x3f3f3f3f;
const ll INF=0x3f3f3f3f3f3f3f3f;

//Data
const int N=5e5;
int n;
char s[N+7];
ll ans;

//SuffixAutomata
const int T=(N<<1);
int cnt=1,en=1,ch[T+7][26],fa[T+7],dep[T+7],sz[T+7];
int c[T+7],q[T+7];
void insert(int c){
    int p=en,np=++cnt;
    dep[en=np]=dep[p]+1;
    for(;p&&!ch[p][c];p=fa[p]) ch[p][c]=np;
    if(!p) fa[np]=1;
    else {
        int q=ch[p][c];
        if(dep[q]==dep[p]+1) fa[np]=q;
        else {
            int nq=++cnt;
            dep[nq]=dep[p]+1;
            memcpy(ch[nq],ch[q],sizeof ch[q]);
            fa[nq]=fa[q],fa[q]=fa[np]=nq;
            for(;ch[p][c]==q;p=fa[p]) ch[p][c]=nq;
        }
    }
    sz[np]=1;
}
void run(){
    for(int i=1;i<=cnt;i++) c[i]=0;
    for(int i=1;i<=cnt;i++) c[dep[i]]++;
    for(int i=1;i<=cnt;i++) c[i]+=c[i-1];
    for(int i=1;i<=cnt;i++) q[c[dep[i]]--]=i;
    for(int i=cnt;i>=1;i--){
    	int p=q[i];
        sz[fa[p]]+=sz[p];
        ans+=1ll*(dep[p]-dep[fa[p]])*sz[p]*(n-sz[p]);
    }
}

//Main
int main(){
	scanf("%s",&s[1]),n=strlen(&s[1]);
	for(int i=1;i<=n;i++) insert(s[i]-'a');
	run();
	printf("%lld\n",ans);
    return 0;
}

---

祝大家学习愉快！