loj10153二叉苹果树

有一棵二叉苹果树，如果数字有分叉，一定是分两叉，即没有只有一个儿子的节点。这棵树共 N 个节点，标号 1 至 N，树根编号一定为 1。

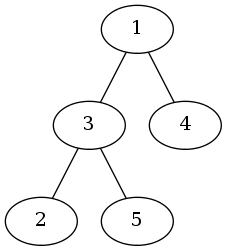
我们用一根树枝两端连接的节点编号描述一根树枝的位置。一棵有四根树枝的苹果树，因为树枝太多了，需要剪枝。但是一些树枝上长有苹果，给定需要保留的树枝数量，求最多能留住多少苹果。

输入格式

第一行两个数 N 和 Q ，N 表示树的节点数，Q 表示要保留的树枝数量。

接下来 N−1 行描述树枝信息，每行三个整数，前两个是它连接的节点的编号，第三个数是这根树枝上苹果数量。

输出格式

输出仅一行，表示最多能留住的苹果的数量。

样例

样例输入

5 2
1 3 1
1 4 10
2 3 20
3 5 20

样例输出

21

数据范围与提示

对于 100% 的数据，1≤Q≤N≤100,N≠1，每根树枝上苹果不超过 30000 个。

————————————————————————————————————————————————————

树形动归，

开始写的是首先把树变成二叉树，然后动归，记过严重超时，69分，直接在树上进行动归，就可以了，而且时间快很多！！

————————————————————————————————————————————————————

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int maxn=105;
 4 struct edge
 5 {
 6     int u,v,w,nxt;
 7 }e[maxn<<1];
 8 int head[maxn],js;
 9 int n,m;
10 int f[maxn][maxn];
11 struct node
12 {
13     int w,lc,rc;
14 }tree[maxn];
15 int lc[maxn],rc[maxn],ww[maxn];
16 inline void addage(int u,int v,int w)
17 {
18     e[++js].u=u;e[js].v=v;e[js].w=w;
19     e[js].nxt=head[u];head[u]=js;
20 }
21 int dfs(int u,int fa,int s)
22 {
23     if(s==1)return f[u][s]=ww[u];
24     if(s==0)return 0;
25     if(f[u][s]>0)return f[u][s];
26     for(int i=head[u];i;i=e[i].nxt)
27     {
28         int v=e[i].v;
29
30         if(v!=fa)
31         {
32             ww[v]=e[i].w;
33             if(lc[u]==0)lc[u]=v;
34             else rc[u]=v;
35             for(int j=0;j<s;++j)
36             {
37                 dfs(v,u,j);
38             }
39         }
40     }
41     for(int i=0;i<s;++i)
42         f[u][s]=max(f[u][s],f[lc[u]][i]+f[rc[u]][s-i-1]+ww[u]);
43     return f[u][s];
44 }
45 void readint(int &x)
46 {
47     x=0;
48     char c=getchar();
49     for(;c>'9'||c<'0';c=getchar());
50     for(;c>='0' && c<='9';c=getchar())x=x*10+c-'0';
51 }
52 int main()
53 {
54     readint(n);readint(m);
55     for(int u,v,w,i=1;i<n;++i)
56     {
57         readint(u);readint(v);readint(w);
58         addage(u,v,w);
59         addage(v,u,w);
60     }
61     dfs(1,0,m+1);
62     cout<<f[1][m+1];
63     return 0;
64 }