tarjan复习笔记 双连通分量，强连通分量

声明：图自行参考割点和桥QVQ

双连通分量

• 如果一个无向连通图\(G=(V,E)\)中不存在割点（相对于这个图），则称它为点双连通图

• 如果一个无向连通图\(G=(V,E)\)中不存在割边（相对于这个图），则称它为边双连通图

• 无向图的极大点双连通子图称为点双连通分量，简称\(v-DCC\)

• 无向图的极大边双连通子图称为边双连通分量，简称\(e-DCC\)

• 如果称一个双连通子图\(G'=(V',E')\)极大，当且仅当不存在\(G\)的另外一个子图\(G''=(V'',E'')\neq G'\),使得\(G'\)是\(G''\)的子图且\(G''\)是双连通子图

\(e-DCC\)（边双）

求法

• 删除原图中所有的桥，剩下的连通块均为\(e-DCC\).

• 先用\(Tarjan\)标记所有的桥，在DFS每个连通块，给各个点分配所在的\(e-DCC\)的编号即可

缩点法

• 在有些具有特殊性质的问题中，可以把一个\(e-DCC\)看做一个点进行处理

• 可以考虑一下求得所有的\(e-DCC\)，然后建一张新图，仅保留所有的\(e-DCC\)和桥

• 这种将一个双连通分量收缩为一个节点的方法称为缩点

• 代码实现中我们可以把每一个边双的编号看做是节点编号，如果两个边双之间有桥，那么在新图中在这两个点之间连边即可

• 新图是一棵树或者森林

代码简述（求无向图中的桥，边双连通分量，并进行缩点）

void tarjan(int x,int in_edge)
{
	low[x]=dfn[x]=++poi;
	for(int i=head[x];i;i=e[i].last)
	{
		int y=e[i].to;
		if(!dfn[y])
		{
			tarjan(y,i);
			low[x]=min(low[x],low[y]);
			if(low[y]>dfn[x])
				bridge[i]=bridge[i^1]=1;
		}
		else if(i!=(in_edge^1))//如果这个边不是上次的反向边
			 low[x]=min(low[x],dfn[y]);
	}
}

首先根据\(Tarjan\)求桥的原理\(dfn[n]<low[y]\)求出桥，但是要注意的是这是双向边，所以正边和反边都要打标记，在这里我们可以用位运算"^"实现反边的操作，奇-1,偶+1

void dfs(int x)
{
	c[x]=dcc;
	for(int i=head[x];i;i=e[i].last)
	{
		int y=e[i].to;
		if(c[y]||bridge[i]) continue;//如果这个点已经有了存储的值或者这条边是桥就不进行
		//是桥的话要是弄进去那说明这个子图中就有桥了。不符合
		dfs(y);
	}
}

然后用深搜给每个都进行标号，如果这个点是已经有编号了或者该边是桥，那么就继续找

int main()
{
	int n,m;
	cin>>n>>m;
	cnt=1;//保证运算简便，边的编号从2开始
	for(int i=1;i<=m;i++)
	{
		int x,y;
		cin>>x>>y;
		add(x,y);
		add(y,x);
	}
	for(int i=1;i<=n;i++)
		if(!dfn[i]) tarjan(i,0);//“^”运算，奇数-1，偶数+1
	for(int i=2;i<cnt;i+=2)
		if(bridge[i])
			cout<<e[i^1].to<<" "<<e[i].to<<endl;
	for(int i=1;i<=n;i++)
	{
		if(!c[i])
		{
			++dcc;
			dfs(i);
		}
	}
	cout<<"There are "<<dcc<<" e-DCCs"<<endl;
	for(int i=1;i<=n;i++)
	{
		cout<<i<<" belongs to DCC "<<c[i]<<endl;
	}
	c_cnt=1;//边还是从2开始，便于计数
	for(int i=2;i<=cnt;i++)
	{
		int x=e[i^1].to;
		int y=e[i].to;
		if(c[x]==c[y])continue;
		c_add(c[x],c[y]);//缩点建图
	}
	cout<<"缩点以后的森林，点数为 "<<dcc<<" 边数为 "<<c_cnt/2<<endl;
	for(int i=2;i<c_cnt;i++)
	{
		cout<<ce[i^1].to<<" "<<ce[i].to<<endl;
	}
	return 0;
}

• 主函数里面，首先我们把边的计数值设为\(1\),那么边的编号就是从\(2\)开始，便于用"^"进行运算
• 然后先进行\(Tarjan\)把所有的桥找出来，进行深搜
• 当然因为是双向的，所以反向边一块处理了即可，都标记为桥
• 然后就开始进行标号啦，深搜进行标号
• 然后我们就可以计算出有多少个边双连通分量以及他们的从属关系
• 然后就开始建立新的图，编号还是从2开始，便于计算
• 至于为什么只建立有向边，因为这个编号是+1+1处理的，它的反向边一定会建立
• 最后就看结果就好啦QVQ

\(v-DCC\)（点双）

上图!

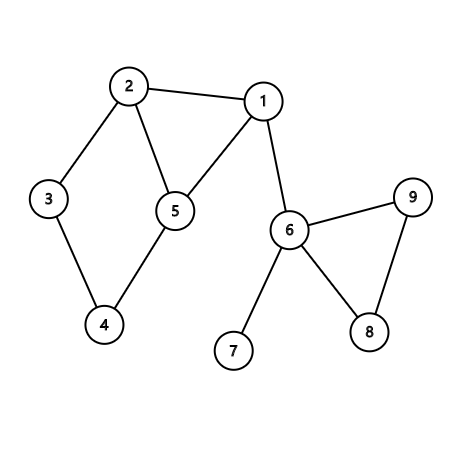
求法

• 如果一个点被孤立了，那么它就自己构成一个点双，否则点双的大小至少为\(2\)

• 一个割点可以被多个点双包含，其余点只能在一个点双里面

• 看上面的图，图中的割点为\(1,6\)

-图中的点双为\([1,2,3,4,5],[1,6],[6,7],[6,8,9]\)

• 得出构造方法
  
  1、先在原图中削除所有的割点
  
  2、枚举剩下的所有连通块，然后向每一个连通块中添加原图中与该连通块相连的割点
  
  3、然后一个点双就诞生了

• 于是伟大的哲人"他姐"发明了一个基于栈的做法

• 我们可以在\(Tarjan\)的过程中维护一个栈，并且按照如下的元素维护
  
  1、当一个节点第一次被访问到时，入栈
  
  2、当搜到一个节点\(x\)且发先一个儿子\(y\)满足割点法则\(dfn_x<=low_y\)时，无论\(x\)是否为根，都要从栈顶不断弹出栈，然后直到\(y\)出栈，并将刚才的元素与\(x\)共同构成一个点双
  
  3、用vector维护即可

缩点法

• 保留割点，并且将所有的点双都缩成一个点

• 每个点双向自身包含的割点中进行连边

• 如果原图中一共有\(x\)个割点，\(y\)个点双，新图中一共有\(x+y\)个点

• 新图中是一个树或者是森林

代码实现

void tarjan(int x)
{
	dfn[x]=low[x]=++poi;
	suk[++top]=x;//将第一遍搜过的点入栈
	if(x==root&&head[x]==0)//判断孤立点
	{
		dcc[++sum].push_back(x);
		return;
	}
	int flag=0;
	for(int i=head[x];i;i=e[i].last)
	{
		int y=e[i].to;
		if(!dfn[y])
		{
			tarjan(y);
			low[x]=min(low[x],low[y]);
			if(low[y]>=dfn[x])//如果这是一个割点
			{
				flag++;
				if(x!=root||flag>1) cut[x]=1;//割点
				int z;
				sum++;
				do{
					z=suk[top--];
					dcc[sum].push_back(z);
				}while(z!=y);
				dcc[sum].push_back(x);//形成一个新的v-DCC
			}
		}
		else low[x]=min(low[x],dfn[y]);
	}
}

首先还是进行\(Tarjan\)处理,求出每个点双并且将割点标记。

int main()
{
	cin>>n>>m;
	cnt=1;
	for(int i=1;i<=m;i++)
	{
		int x,y;
		cin>>x>>y;
		if(x==y) continue;
		add(x,y);
		add(y,x);
	}
	for(int i=1;i<=n;i++)
	{
		if(!dfn[i])
		{
			root=i;
			tarjan(i);
		}
	}
	for(int i=1;i<=n;i++)
	{
		if(cut[i])
		cout<<i<<" ";
	}
	cout<<"are cut-vertexes"<<endl;
	for(int i=1;i<=sum;i++)
	{
		cout<<"e-DCC #"<<i<<": ";
		for(int j=0;j<dcc[i].size();j++)
		{
			cout<<dcc[i][j]<<" ";
		}
		cout<<endl;
	}
	int js=sum;
	for(int i=1;i<=n;i++)
	{
		if(cut[i])
		new_id[i]=++js;//建立新的
	}
	c_cnt=1;//从2开始方便计算
	for(int i=1;i<=sum;i++)// 建新图，从每个v-DCC到它包含的所有割点连边
	{
		for(int j=0;j<dcc[i].size();j++)
		{
			int x=dcc[i][j];
			if(cut[x])
			{
				c_add(i,new_id[x]);
				c_add(new_id[x],i);
			}
			else c[x]=i;
		}
	}
	cout<<"缩点后的森林，点数为"<<js<<" 边数为 "<<c_cnt/2<<endl;
	printf("编号 1~%d 的为原图的v-DCC，编号 >%d 的为原图割点\n", sum, sum);
	for(int i=2;i<c_cnt;i+=2)
		printf("%d %d ",ce[i^1].to,ce[i].to);
	return 0;
}

然后就是庞大的主函数了（提醒一下，在我的理解中root应该只出现在求割点的时候，其他时候基本木有）

• 首先，初始值设为1，编号从\(2\)开始建立双边（如果是单向的你也要建立，因为割点只存在于无向图中）
• 然后进行\(Tarjan\)处理
• 当我们找完的时候，所有的点双和割点都已经被我们求出来啦
• 然后我们就可以愉快的找出每一个点双里的元素
• 此时，我们的所有点双已经被标完编号了，然后就开始给所有的割点建立新编号\(new-id\)
• 建立完以后还是编号从\(2\)开始分别找每个点双里面的割点，然后向他连双向边，然后把其他不是割点的点统计一下所在的点双编号
• 最后输出就好了！完美结束

强连通分量

• 对于一个有向图，若关于任意的两节点\(x,y\)，既存在从\(x\)到\(y\)的路径，同时也存在\(y\)到\(x\)的路径,则称该有向图是强连通图。

• 对于有向图的极大强连通子图称为强连通分量，记为\(SCC\)

• \(Tarjan\)算法能够在线性时间内求解有向图所有的强连通分量

特殊定义

• 给定一个有向图\(G=(V,E)\),存在\(r\in V\)，\(r\)能到达\(V\)中的任何点，则称\(G\)是一个流图，记为\((G,r)\),\(r\)称作\(G\)的源点

• 与无向图类似，在流图上从\(r\)出发开始DFS，每个节点只访问一次

• 所有发生递归的边构成一棵以\(r\)为根的树，称之为流图\(（G,r）\)的搜索树

• 按照每个节点第一次访问的时间顺序依次标号，该整数标号称为时间戳，记为\(dfs_x\)

流图中的边

• 流图中的有向边\((x,y)\)一定是一下四种之一：
  
  1、树枝边，搜索树上的
  
  2、前向边，不存在于搜索树上，且在搜索树中\(x\)是\(y\)的祖先
  
  3、后向边，不存在与搜索树上，且在搜索树中\(y\)是\(x\)的祖先
  
  4、横叉边，不是上述三种情况的边，那么一定有\(dfn_y<=\)dfn_x,否则会在DFS的时候经过\(y\)从而构成树枝边

• 看图理解一下
  
  

SCC的求法

定义梳理

• 根据定义，这一定是一个环，那么所有的环一定是强连通图

• \(Tarjan\)算法的基本思路就是对于每一个点，都尽量找到与它一起能构成环的所有节点

不同的边的贡献

• 对于一条边\((x,y)\)我们讨论一下他的类型
  
  1、前向边，对找环没有用，因为在搜索树中本来就存在\(x->y\)的路径
  
  2、后向边，对找环很有用，因为在搜索树中可以和\(x->y\)的路径构成一个环
  
  3、横叉边，对找环可能有用，如果从\(y\)出发能找到一条路径回到\(x\)的祖先节点，则可以构成一个环，它就是有用的

遍历

• 为了找到通过后向边和横叉边构成的环，\(Tarjan\)算法在DFS是维护一个栈

• 当第一次访问到这个点时，入栈

• 访问到\(x\)时，栈中保存了一下的两类点：
  
  1、搜索树上\(x\)的祖先节点
  
  2、已经访问过，存在一条路径能够到达\(x\)的祖先的点

• 这些节点都存在一条到达\(x\)的路径，如果\(x\)也能到达他们，那么就构成了一个环

追溯值

• 可以理解为\(x\)的搜索子树上\(x\)能到达的时间戳最小的能到达\(x\)的点

构建方法

• 当第一次访问到\(x\)是，首先令\(low_x=dfn_x\)

-在考虑与\(x\)相连的每一条边，DFS回溯的时候更新\(low_x\)

• 如果\(y\)没有被访问，那么就递归的访问，则\(low_x=min(low_x,low_y)\)

• 但如果\(y\)在栈中，那么\(low_x=min(low_x,dfn_y)\)

• (重点)当\(x\)回溯以前，首先先判断是否有\(low_x=dfn_x\)

• 如果有，那么久不断弹栈直到\(x\)出栈

• 弹栈的所有节点构成了一个SCC

构建理解

• 当我们回溯完毕时，已经考虑了\(x\)能到达的所有节点

• \(y\)被访问过并且不再栈中:\(x\)能达到\(y\),但\(y\)无法到达\(x\)

• 由回溯完毕可知已经考虑了所有\(y\)能到达的节点，所以如果\(y\)能到达\(x\)，那么\((x,y)\)不会是横叉边，所以\(y\)对\(low_x\)没有贡献

缩点法

• 将所有的强连通分量看做一个节点

• 将每个\(SCC\)的编号看做节点的编号，如果两个强连通分量之间有有向边，那么在新图中这两个点之间连上同一个方向的边即可

• 缩掉所有的环之后，就会得到一张DAG，我们就可以在上面做处理

代码实现

void tarjan(int x)
{
	low[x]=dfn[x]=++poi;
	suk[++top]=x;
	ins[x]=1;
	for(int i=head[x];i;i=e[i].last)
	{
		int y=e[i].to;
		if(!dfn[y])
		{
			tarjan(y);
			low[x]=min(low[x],low[y]);
		}
		else if(ins[y])
		low[x]=min(low[x],dfn[y]);
	}
	if(low[x]==dfn[x])
	{
		sum++;
		int y;
		do{
			y=suk[top--];
			ins[y]=0;
			c[y]=sum;
			scc[sum].push_back(y);
		}while(x!=y);
	}
}

首先进行\(Tarjan\)求出所有的量，然后在回溯之前判断一下即可

int main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		int x,y;
		cin>>x>>y;
		add(x,y);
	}
	for(int i=1;i<=n;i++)
	{
		if(!dfn[i])
			tarjan(i);
	}
	for(int x=1;x<=n;x++)
	{
		for(int i=head[x];i;i=e[i].last)
		{
			int y=e[i].to;
			if(c[x]==c[y]) continue;
			c_add(c[x],c[y]);
		}
	}
}

在主函数中，遍历完一遍以后，开始枚举每个点的所有编号，根据有向图的变得方向进行建边

例题

P3387 P3388 P2341 P3469 P2194 P1262

P1262 P2002 P2746 P5058