土题大战Vol.0 A. 笨小猴 思维好题

土题大战Vol.0 A. 笨小猴 思维好题

题目描述

驴蛋蛋有 \(2n + 1\) 张 \(4\) 星武器卡片，每张卡片上都有两个数字，第 \(i\) 张卡片上的两个数字分别是 \(A_i\) 与 \(B_i\)。

现在驴蛋蛋要从所有卡片中选出恰好 \(n + 1\) 张卡片，然后计算他选出的所有卡片中 \(A_i\) 的和与 \(B_i\) 的和。他的目的是要使他选出的卡片的\(A_i\) 的和与 \(B_i\) 的和，都要分别大于剩下 \(n\) 张没选的卡片的 \(A_i\) 的和与 \(B_i\) 的和。

驴蛋蛋最近沉迷于周年挑战赛，所以他希望你能帮他解决这个问题。

输入格式

输入第一行是一个整数 \(n\)，意义如以上所示。

接下来有 \(2n + 1\) 行，每行为两个正整数，第 \(i\) 行的两个正整数分别代表 \(A_i\) 和 \(B_i\)。

输出格式

如果无法选出 \(n + 1\) 张卡片满足驴蛋蛋的要求，输出一个数 \(-1\)。

否则输出 \(n + 1\) 行，每 行有一个正整数，表示选出的卡片编号（从 \(1\) 开始）。如果有多解，输出任意一组解均可

样例

样例输入

2

4 2

9 4

5 3

7 5

8 1

样例输出

3

4

2

样例解释

选择顺序随意，选择第二，三，四张三张卡片，\(A\)的总和为\(21\)，\(B\)的总和为\(12\)，均大于剩下的卡片\(A\)，\(B\)之和。

数据范围与提示

共\(10\)组测试数据

对于前\(3\)组测试数据有第\(p\)组中\(N=2 \times p+1\)

对于后7组测试数据有第\(p\)组中\(N=p\times 10000\)

对所有测试数据\(1 \leq A_i,B_i \leq 10^9\)

如果你通过某种方法\(hack\)掉了评测插件，你可以申请获得该测试点的分数\(=ω=\)

分析

先画一个图便于理解

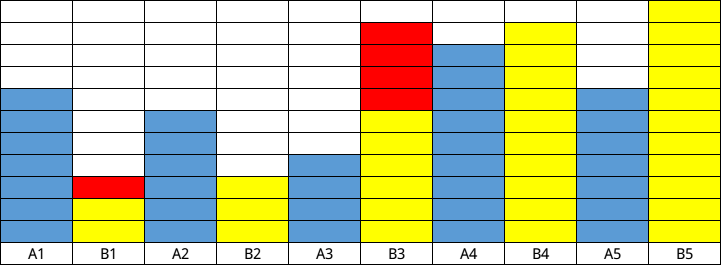
我们先按照\(B\)的值从小到大排序，把序列中的最后一个元素单独拿出来选上，剩下的两两一组

在两两一组中，我们选取\(A\)的值较大的那一个，这样我们就可以把\(A\)元素的条件满足

对于\(B\)元素来说，我们选择的元素的差值是图中红色的部分

我们会发现，在最坏的情况下，红色部分拼起来的总和也不会超过最后一个元素的\(B\)值

也就是说，我们选择的\(B\)元素的值一定大于剩下的\(B\)元素的值

所以，我们只需要简单排序即可

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+5;
typedef long long ll;
ll pja,pjb;
struct asd{
	ll xx,yy;
	int bh;
}b[maxn];
bool cmp(asd aa,asd bb){
	return aa.yy<bb.yy;
}
int n,m,top,sta[maxn];
int main(){
	scanf("%d",&n);
	m=n*2+1;
	for(int i=1;i<=m;i++){
		scanf("%lld%lld",&b[i].xx,&b[i].yy);
		b[i].bh=i;
	}
	sort(b+1,b+1+m,cmp);
	m--;
	for(int i=1;i<=m;i+=2){
		if(b[i].xx>b[i+1].xx) sta[++top]=b[i].bh;
		else sta[++top]=b[i+1].bh;
	}
	sta[++top]=b[m+1].bh;
	for(int i=1;i<=top;i++){
		printf("%d\n",sta[i]);
	}
	return 0;
}