P、NP、NPC问题详解

转载地址

https://blog.csdn.net/bcb5202/article/details/51202589

P、NP、NPC

---

概念

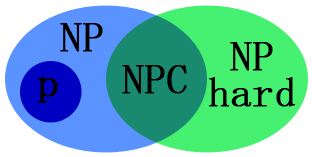
> P问题：能够在多项式时间内解决的决策问题。

—举例: 图搜索问题、最短路径问题、最小生成树问题······

---

> NP问题：不能在多项式时间内解决或不确定能不能在多项式时间内解决，但能在多项式时间验证的问题。

—验证：给定一个问题的实例、证书（类似于证据），需要验证这个证书是这个问题的正确答案。

— 举例：汉密尔顿路径，实例为G=(V,E)，证书为顶点序列 {v0,v1,v2,v3,….,vk}，我们的目的是要验证这个证书就是这个问题的答案，验证方法为：先遍历一遍这个点序列，看看是不是每个点只出现一次，然后对于(vi,vi+1)是否为G的边，这样就能够验证这个点序列是不是汉密尔顿路径，很显然这个验证过程是多项式时间的，所以汉密尔顿路径是NP问题。

---

> NPC问题：目前不能用多项式时间解决的问题，但是我们还不能证明这个问题不能用多项式时间解决，我们这次的目标是研究这个问题。

—满足的两个条件：是一个NP问题 + 所有的NP问题可以在多项式时间内规约到它

—举例：3SAT、顶点覆盖、团、三维匹配、汉密尔顿回路、划分问题·······

---

> NP难问题：所有的NP问题可以在多项式时间归约到它，但它不一定是一个NP问题

---

> 归约(约化)的标准概念： 如果能找到这样一个变化法则，对程序A的任意一个输入，都能按这个法则变换成程序B的输入，使这两个程序的输出相同，那么我们说，问题A可归约为问题B

— 问题A可以约化到问题B的含义是，可以用解决B的解法来解决A，或者说A可以“变成”B。

—A可归约为B的直观含义：B的时间复杂度>=A的时间复杂度。也即，A比B简单。

---

关系

P、NP、NPC、NP Hard问题的关系如下：

---

证明NPC问题

证明问题B是NPC问题的过程如下：

1. 证明B是NP问题
2. 知道一个已知的NPC问题A
3. 证明A归约到B。

---

常见归约问题

基本知识

1、独立集 —— 在图G = （V，E）中，如果顶点集合S⊆V中的任意两点之间都没有边，则称S是独立的。

—难点： 寻找最大独立集。

—目标： 装入尽可能多的顶点，要求边涉及到的边服从一些限制条件。

---

2、顶点覆盖 —— 给定图G = （V，E），顶点集合S⊆V，如果图中的每一条边至少有一个端点在S中，则称S是一个顶点覆盖。

—难点： 寻找最小顶点覆盖。

—目标： 用尽可能少的顶点覆盖图中的所有边。

---

3、集合覆盖 —— 试图用一组较小的集合覆盖一个任意的对象集合。

---

常见问题

1、独立集问题——给定图G和数k，问是否包含大小至少为k的独立集？

---

2、顶点覆盖问题——给定图G和数k，问G是否包含大小至多为k的顶点覆盖？

---

3、集合覆盖问题——给定n个元素的集合U，U的子集S1，···，Sm以及数k，问在这些子集中有一组子集，它们的并等于整个U且至多包含k个子集吗？

---

4、集合包装问题——给定n个元素的集合U，U的子集S1，····，Sm以及数k，问在这些子集中至少有k个两两不相交吗？

---

5、SAT(可满足性问题)——给定bool变量集X={x1，···，xn}上的一组子句C1，···，Ck，问存在满足的真值赋值吗？

注意：每个子句均为析取子句(逻辑或∨)，最终结果为各个子句的合取(逻辑与∧)。

---

6、3-SAT(三元可满足性问题)——给定bool变量集X={x1，···，xn}上的一组子句C1，···，Ck，每个子句的长为3，问存在满足的真值赋值吗？

注意：同上。

---

常用引理

设G=(V, E)是一个图，S⊆V，那么S是一个独立集当且仅当它的补V-S是一个顶点覆盖。

证明：首先，设S是一个独立集。考虑任一边e=(u,v)，因为S是独立集，u和v不可能同时在S中，所以u和v至少有一个在V-S中，即得任一边至少有一个端点在V-S中，所以V-S是一个顶点覆盖。

反过来，设V-S是一个顶点覆盖，考虑S中的任意两个顶点u、v，若它们间有一条边e，那么e的两个端点均不在V-S中，这与假设V-S是一个顶点覆盖矛盾。所以S中的任意两点均无连线，所以S是一个独立集。

---

常见归约问题

归约的一般思想(要点)：证明Y到X的归约，要用问题X中的分量构造“零件”来描写在问题Y中正在做的事

1、 独立集归约到顶点覆盖

证明：若有一个解顶点覆盖的黑盒子，那么通过问黑盒子G是否有大小至多为n-k的顶点覆盖，就能确定G是否有大小至少为k的独立集。

---

2、顶点覆盖归约到独立集

证明：若有一个可以解独立集的黑盒子，那么通过问黑盒子G是否有大小至少为n-k的独立集，就能确定G是否有大小至多为k的顶点覆盖。

---

3、顶点覆盖归约到集合覆盖

证明：若有一个可以解集合覆盖的黑盒子，考虑顶点覆盖的任一实例，给定图G=(V, E)和数k。

构造集合覆盖的一个实例，其基集U等于边E，对图G的每一个顶点i∈V，设Si⊆U为G中所有和点i相关联的边，把Si加入集合覆盖的实例中。

U能被集合S1,S2,···,Sn中的至多k个覆盖当且仅当G有大小至多为k的顶点覆盖。于是，给定顶点覆盖的实例，如上述的那样构造集合覆盖的实例，并把它输入黑盒子。回答yes当且仅当黑盒子回答yes。

---

4、独立集归约到集合包装

证明：若有一个解集合包装的黑盒子，考虑独立集的任一实例，给定图G=(V,E)和数k。

构造集合包装的一个实例，其基集U等于边E，对图G的每一个顶点i∈V，设Si⊆U为G中所有不和点i相关联的边，把Si加入集合包装的实例中。

U的子集S1，S2，···，Sn(实际是n个边集合)中至少k个两两不相交(即不存在相同边)当且仅当G有大小至少为k的独立集(此时k个顶点必不存在相连边)，于是，给定独立集的实例，如上述的那样构造集合包装的实例，并把它输入黑盒子。回答yes当且仅当黑盒子回答yes。

---

5、3-SAT归约到独立集

证明：设有一个解独立集的黑盒子，要解3-SAT的实例，实例由变量集X={x1，····，xn}和子句C1，····，Ck组成。

考虑3-SAT的方法是：必须从每一个子句中选择一个项，然后找一组真值赋值使得所有找出来的项都为1，从而满足所有的子句。因此，如果如果没有两个被选中的项冲突，那么就成功了。

具体归约：用独立集描述3-SAT实例。首先，构造图G=(V,E)，它由分成k个三角形的3k个顶点组成，如下图所示。对每一个子句i，构造3个顶点vi1，vi2，vi3。依据3-SAT实例子句在图中增加边描述冲突：在每一对标号对应冲突的项的顶点间添加一条边。



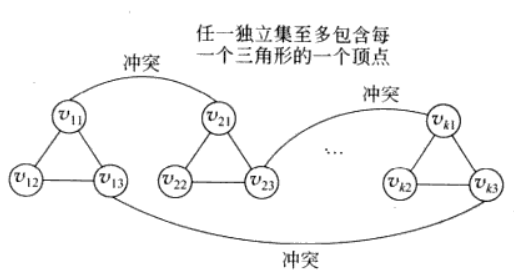
要证明原来的3-SAT是可满足的当且仅当构造出来的图G(依据3-SAT的实例子句构造)有大小至少为k的独立集。

>首先，若3-SAT是可满足的，那么构造出来的图G中的每个三角形至少包含一个标号的值为1的顶点。设S是每一个三角形中的一个这样的顶点组成的集合。设S不是一个独立集，则至少存在两个顶点u、v∈S间有一条边，则u、v一定是冲突(一个是1，另一个必是0)的，而S中的每个点值都为1，所以矛盾，所以假设不成立，即S是一个独立集。

>反过来，设图G有一个大小至少为k的独立集S。那么，当S的大小恰好为k，那么一定是由每个三角形的一个顶点组成，且S中的冲突顶点最多只能成单出现。所以显然可以设S中所有顶点对应的值全为1，且这些顶点每个对应于一个子句中选择的代表，所以此时对应的3-SAT实例存在真值赋值。