Codeforces Round #646 (Div. 2) B. Subsequence Hate (思维,前缀和)

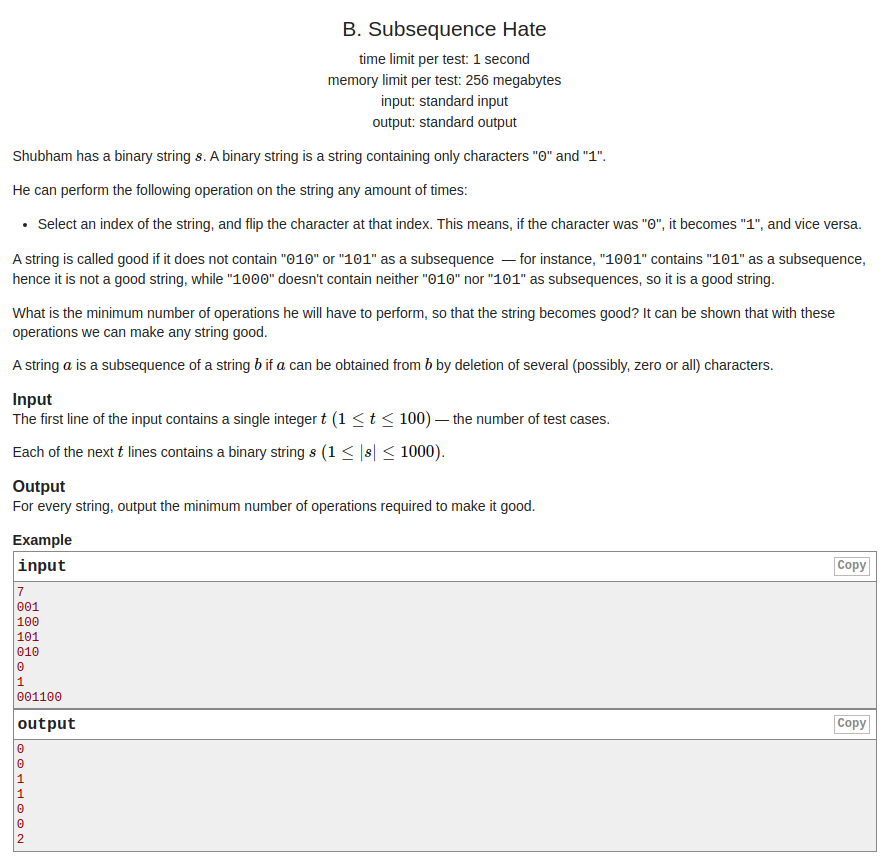
• 题意:给你一个只含有\(0\)和\(1\)的字符串,每次操作可以将\(0\)改成\(1\)或\(1\)改成\(0\),问最少操作多少次,使得子序列中不含有\(010\)和\(101\).

• 题解:仔细想一想不难发现,构造后的字符串要么全是\(1\)和\(0\),要么就是\(000....111\)和\(111...000\),我们对\(0\)求一个前缀和,判断一下这些情况,更新最小值即可.

• 代码:

  #include <iostream>
  #include <cstdio>
  #include <cstring>
  #include <cmath>
  #include <algorithm>
  #include <stack>
  #include <queue>
  #include <vector>
  #include <map>
  #include <set>
  #include <unordered_set>
  #include <unordered_map>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  const int N = 1e6 + 10;
  const int mod = 1e9 + 7;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  int t;
  int pre[N];
  string s;
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);
      cin>>t;
       while(t--){
           cin>>s;
           s=" "+s;
           me(pre,0,sizeof(pre));
           int len=s.size();
           int cnt0=0,cnt1=0;
           for(int i=1;i<len;++i){
               if(s[i]=='0'){
                   cnt0++;
                   pre[i]=pre[i-1]+1;
               }
               else{
                   cnt1++;
                   pre[i]=pre[i-1];
               }
           }
           int ans=min(cnt0,cnt1);
           for(int i=1;i<len;++i){
               ans=min(ans,pre[i]+(len-1-i-(pre[len-1]-pre[i])));
           }
           for(int i=1;i<len;++i){
               ans=min(ans,i-pre[i]+pre[len-1]-pre[i]);
           }
           printf("%d\n",ans);
       }
      return 0;
  }