洛谷 P1131 [ZJOI2007]时态同步 树形DP

题目描述

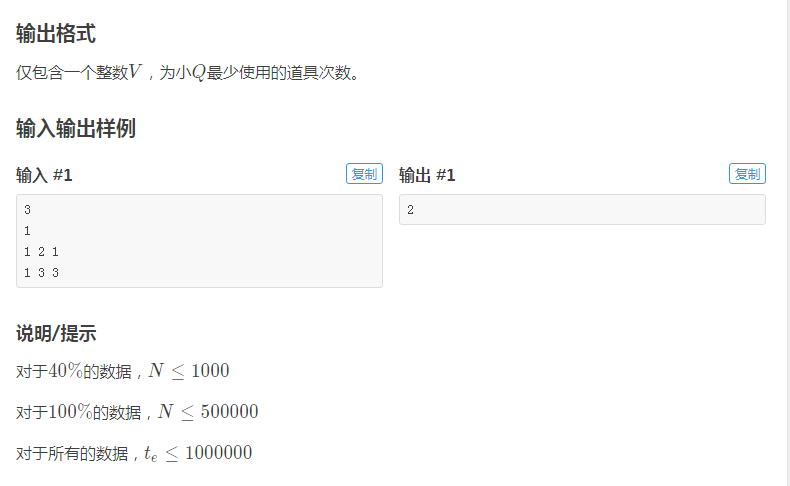
分析

我们从根节点开始搜索，搜索到叶子节点，回溯的时候进行维护

先维护节点的所有子节点到该节点最大边权（边权为叶子节点到同时到达它所需要时间）

然后维护答案，答案为最大边权减去所有到子节点的边权。

然后维护父节点的边权，父节点边权为该节点子节点的 最大边权+父节点到该节点的时间。

然后就回溯，重复操作，到根节点为止。

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e6+5;
typedef long long ll;
struct asd{
    int from,to,next;
    ll val;
}b[maxn];
int head[maxn],tot=1;
void ad(int aa,int bb,ll cc){
    b[tot].from=aa;
    b[tot].to=bb;
    b[tot].next=head[aa];
    b[tot].val=cc;
    head[aa]=tot++;
}
ll f[maxn];
ll sum[maxn],ans[maxn];
ll siz[maxn];
void dfs(int now,int fa){
    for(int i=head[now];i!=-1;i=b[i].next){
        int u=b[i].to;
        if(u==fa) continue;
        dfs(u,now);
        sum[now]=max(sum[now],b[i].val+sum[u]);
    }
}//第一遍dfs求出修改后m节点到叶子节点的权值之和
void dfs2(int now,int fa){
    for(int i=head[now];i!=-1;i=b[i].next){
        int u=b[i].to;
        if(u==fa) continue;
        f[now]+=sum[now]-sum[u]-b[i].val;
        dfs2(u,now);
        f[now]+=f[u];
    }
}//第二遍dfs求出修改以m节点为根的子树所需要的最小花费
int main(){
    memset(head,-1,sizeof(head));
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<n;i++){
        int aa,bb;
        ll cc;
        scanf("%d%d%lld",&aa,&bb,&cc);
        ad(aa,bb,cc);
        ad(bb,aa,cc);
    }
    dfs(m,0);
    dfs2(m,0);
    printf("%lld\n",f[m]);
    return 0;
}