已知圆的坐标方程为：

X=R*SIN(θ)

Y=R*COS(θ)     （0≤θ≤2π）

将0~2π区间等分48段，即设定间隔dig的值为π/24。θ初始值从0开始，按曲线方程求得坐标值(x,y)，并在当前坐标处绘制一个半径为r（相比R，r小得多）实心圆。之后每隔0.05秒，清除画布，将θ的初始值加π/24后，按曲线方程求得新坐标值(x,y)，并在求得的新坐标处再绘制一个半径为r的实心圆，这样，可以得到半径为r的圆绕半径为R的圆形轨道动态旋转的动画效果。旋转一周后（即θ的值为2π），令θ重新从初值0开始继续动画过程。

编写如下的HTML代码。

<!DOCTYPE html>

<html>

<head>

<title>绕圆周旋转的小球</title>

</head>

<body>

<canvas id="myCanvas" width="500" height="400" style="border:3px double #996633;">

</canvas>

<script type="text/javascript">

var canvas = document.getElementById('myCanvas');

var ctx = canvas.getContext('2d');

var i=0;

setInterval(move,50);

function move()

{

ctx.clearRect(0,0,canvas.width,canvas.height);

var dig=Math.PI/24;

x0=250;

y0=200;

ctx.strokeStyle="green";

ctx.beginPath();

ctx.arc(x0,y0,100,0,Math.PI*2,true);

ctx.closePath();

ctx.stroke();

ctx.beginPath();

var x=100*Math.sin(i*dig)+x0;

var y=100*Math.cos(i*dig)+y0;

ctx.arc(x,y,5,0,Math.PI*2,true);

ctx.closePath();

ctx.fillStyle = "red";

ctx.fill();

i=i+1;

if (i>=48) i=0;

}

</script>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中呈现出如图1所示绕圆周旋转的小球。

图1  绕圆周旋转的小球

图1中圆周轨道只有一条，编写如下的HTML文件，通过二重循环绘制如图2所示的布满整个Canvas的多条圆周轨道。

<!DOCTYPE html>

<html>

<head>

<title>圆周轨道</title>

</head>

<body>

<canvas id="myCanvas" width="500" height="400" style="border:3px double #996633;">

</canvas>

<script type="text/javascript">

var canvas = document.getElementById('myCanvas');

var ctx = canvas.getContext('2d');

var dig=Math.PI/24;

for (k=0;k<=14;k++)

for (n=0;n<=17;n++)

{

x0=30*n;

y0=30*k;

ctx.beginPath();

ctx.strokeStyle="green";

ctx.arc(x0,y0,27,0,Math.PI*2,true);

ctx.closePath();

ctx.stroke();

}

</script>

</body>

</html>

图2  布满画布的多条圆周轨道

仿图1的程序，让每条轨道上都有一个小球在旋转。编写如下的HTML文件。

<!DOCTYPE html>

<html>

<head>

<title>动感小球</title>

</head>

<body>

<canvas id="myCanvas" width="500" height="400" style="border:3px double #996633;">

</canvas>

<script type="text/javascript">

var canvas = document.getElementById('myCanvas');

var ctx = canvas.getContext('2d');

var i=0;

setInterval(move,30);

function move()

{

ctx.clearRect(0,0,canvas.width,canvas.height);

var dig=Math.PI/24;

for (k=0;k<=14;k++)

for (n=0;n<=17;n++)

{

x0=30*n;

y0=30*k;

ctx.beginPath();

ctx.strokeStyle="green";

ctx.arc(x0,y0,27,0,Math.PI*2,true);

ctx.closePath();

ctx.stroke();

var x=27*Math.sin(i*dig)+x0;

var y=27*Math.cos(i*dig)+y0;

ctx.beginPath();

ctx.arc(x,y,3,0,Math.PI*2,true);

ctx.fillStyle = "black";

ctx.closePath();

ctx.fill();

}

i=i+1;

if (i>=48) i=0;

}

</script>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中呈现出如图3所示多个绕圆周旋转的小球。

图3  多个绕圆周旋转的小球

在图3中，所有小球旋转步调一致，整齐划一，缺少动感。如果为各个旋转的小球加上相位，并去掉轨道痕迹。修改HTML文件如下。

<!DOCTYPE html>

<html>

<head>

<title>动感小球</title>

</head>

<body>

<canvas id="myCanvas" width="500" height="400" style="border:3px double #996633;">

</canvas>

<script type="text/javascript">

var canvas = document.getElementById('myCanvas');

var ctx = canvas.getContext('2d');

var i=0;

setInterval(move,30);

function move()

{

ctx.clearRect(0,0,canvas.width,canvas.height);

var dig=Math.PI/24;

for (k=0;k<=14;k++)

for (n=0;n<=17;n++)

{

x0=30*n;

y0=30*k;

var x=27*Math.sin((i+k*2+n*3)*dig)+x0;

var y=27*Math.cos((i+k*2+n*3)*dig)+y0;

ctx.beginPath();

ctx.arc(x,y,3,0,Math.PI*2,true);

ctx.fillStyle = "black";

ctx.closePath();

ctx.fill();

}

i=i+1;

if (i>=48) i=0;

}

</script>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中呈现出如图4所示动感小球。

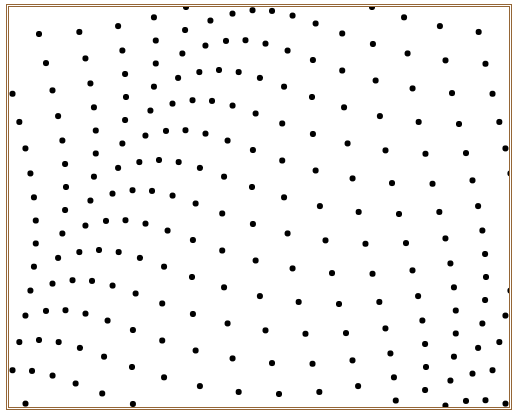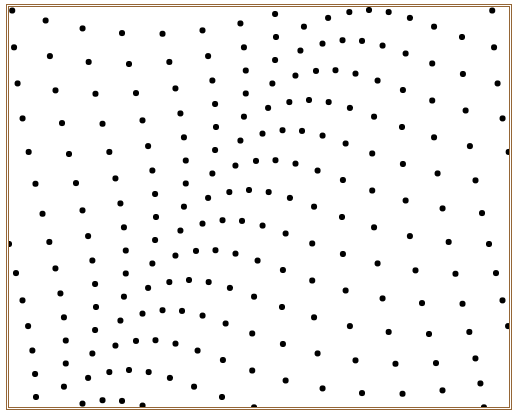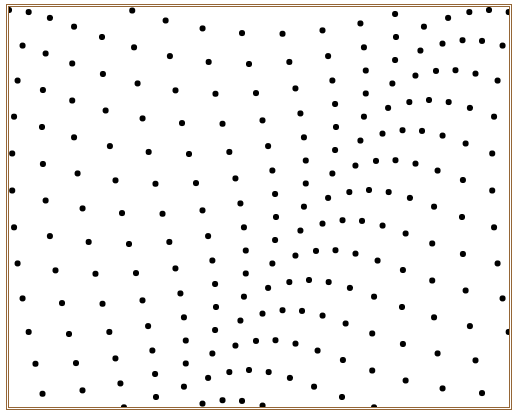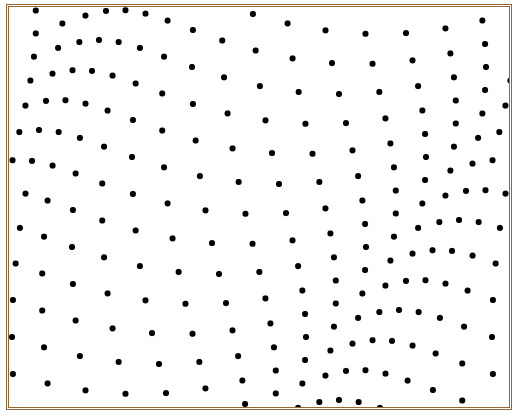
图4 动感小球

JavaScript动画实例：动感小球的更多相关文章

  1. JavaScript动画实例：李萨如曲线

    在“JavaScript图形实例:阿基米德螺线”和“JavaScript图形实例:曲线方程”中,我们学习了利用曲线的方程绘制曲线的方法.如果想看看曲线是怎样绘制出来的,怎么办呢?编写简单的动画,就可以 ...

  2. JavaScript动画实例：递归分形图动态展示

    在“JavaScript图形实例:SierPinski三角形” 和“JavaScript图形实例:Levy曲线及其变形”等文章中我们介绍了通过递归生成分形图形的方法.我们可以将绘制的分形图形每隔一定的 ...

  3. JavaScript动画实例：曲线的绘制

    在“JavaScript图形实例:曲线方程”一文中,我们给出了15个曲线方程绘制图形的实例.这些曲线都是根据其曲线方程,在[0,2π]区间取一系列角度值,根据给定角度值计算对应的各点坐标,然后在计算出 ...

  4. JavaScript动画实例：炸开的小球

    1．炸开的小球 定义一个小球对象类Ball,它有6个属性:圆心坐标(x,y).小球半径radius.填充颜色color.圆心坐标水平方向的变化量speedX.圆心坐标垂直方向的变化量speedY. B ...

  5. JavaScript动画实例：旋转的圆球

    1．绕椭圆轨道旋转的圆球 在Canvas画布中绘制一个椭圆,然后在椭圆上绘制一个用绿色填充的实心圆.之后每隔0.1秒刷新,重新绘制椭圆和实心圆,重新绘制时,实心圆的圆心坐标发生变化,但圆心坐标仍然位于 ...

  6. JavaScript动画实例：旋转的正三角形

    给定一个正三角形的重心坐标为(x0,y0),高为h,可以用如下的语句绘制一个底边水平的正三角形. ctx.beginPath(); ctx.moveTo(x0,y0-h*2/3); ctx.lineT ...

  7. JavaScript动画实例：沿五角星形线摆动的小圆

    五角星形线的笛卡尔坐标方程式可设为: r=10+(3*sin(θ*2.5))^2  x=r*cos(θ) y=r*sin(θ)              (0≤θ≤2π) 根据这个曲线方程,在[0,2 ...

  8. JavaScript动画实例：螺旋线

    数学中有各式各样富含诗意的曲线,螺旋线就是其中比较特别的一类.螺旋线这个名词来源于希腊文,它的原意是“旋卷”或“缠卷”.例如,平面螺旋便是以一个固定点开始向外逐圈旋绕而形成的曲线.在2000多年以前, ...

  9. JavaScript动画实例：运动的字母特效

    已知圆的坐标方程为: X=R*SIN(θ) Y=R*COS(θ)     (0≤θ≤2π) 给定初始坐标位置(X,Y),按照圆的坐标方程,从角度angle = 0开始,每间隔angleSpeed = ...

随机推荐

  1. 用头发换JS的第一天

    因为平时也在上班,这些都是在地铁上抽空开始看的,总结来说还是有一些收获存在,每次看都能发现一些新东西,废话不多说,开撸! JavaScript是一种网页编程语言,可以对网页的行为进行编程,简单来说HT ...

  2. sublime Text3 实现2:1:1三分屏效果

    小trick, 水一篇博客 先上效果图 由于写题啥的时候需要重定向输入输出改数据对拍, 设置成这样的效果就非常直观的看数据 直接切题, 首选项--快捷键--default里搜索alt+shift+1( ...

  3. 浅谈typeof 和instanceof

    typeof vs instanceof 涉及面试题:typeof 是否能正确判断类型?instanceof 能正确判断对象的原理是什么? typeof 对于原始类型来说,除了 null 都可以显示正 ...

  4. 写给大忙人的Redis主从复制，花费五分钟让你面试不尴尬

    相信很多小伙伴都已经配置过主从复制,但是对于redis主从复制的工作流程和常见问题很多都没有深入的了解.咔咔这次用时俩天时间给大家整理一份redis主从复制的全部知识点. 本文实现所需环境 cento ...

  5. 容器技术之Docker Machine

    前文我们聊了下docker容器的资源限制,回顾请参考https://www.cnblogs.com/qiuhom-1874/p/13138725.html:今天我们来聊一聊docker machine ...

  6. 微信小程序-Page生命周期

    QQ讨论群:785071190 微信小程序开发之前我们还需认识一下小程序页面的生命周期,丛"微信小程序-代码构成"一文中我们可以了解到小程序页面中有一个.js的文件,这篇博文我们来 ...

  7. SourceTree使用详解（连接远程仓库，克隆，拉取，提交，推送，新建/切换/合并分支，冲突解决）

    前言: 俗话说的好工欲善其事必先利其器,Git分布式版本控制系统是我们日常开发中不可或缺的.目前市面上比较流行的Git可视化管理工具有SourceTree.Github Desktop.Tortois ...

  8. SpringMVC拦截器使用

    源码地址 拦截器interceptor 拦截器是URL请求的第一道门,所有请求会先经过拦截器interceptor,然后再进入controller: 下面,记录一种通过注解方法拦截所有需要登录才能发起 ...

  9. Java Service Wrapper 浅谈

    在实际开发过程中很多模块需要独立运行,他们并不会以web形式发布,传统的做法是将其压缩为jar包独立运行,这种形式简单易行也比较利于维护,但是 一旦服务器重启或出现异常时,程序往往无法自行修复或重启. ...

  10. JavaWeb网上图书商城完整项目--day02-25.查询所有分类功能之流程分析

    分类模块的业务流程入下面所示: