[MIT6.006] 6. AVL Trees, AVL Sort AVL树，AVL排序

之前第5节课留了个疑问，是关于“时间t被安排进R”的时间复杂度能不能为Ο(log₂n)？”和BST时间复杂度Ο(h)的关系。第6节对此继续了深入的探讨。首先我们知道BST的h是指树的高，即从根到叶子结点最长路径的长度。但由于树结构不同平衡情况，高h的结果也不一样，如下图所示：

 一、结点的高

由此可以看出，平衡树结构下的高h具有计算性。那么接下来我们再看下各结点的高（height of node）的计算方式，它是从该节点位置下到最底部的叶子节点的最长路径长度 （height of node = max(左子树高，右子树高) + 1）：

 二、AVL

我们如果想让Ο(h)=Ο(log₂n)，就必须把BST变为平衡树，但现实中，不一定所有数列都能构成完全的平衡树，但可以构成高度平衡树AVL（由Adelson-Velsky和E.M. Landis发明的），在该树下，每个结点的左右子树相差最多±1。如下图所示：

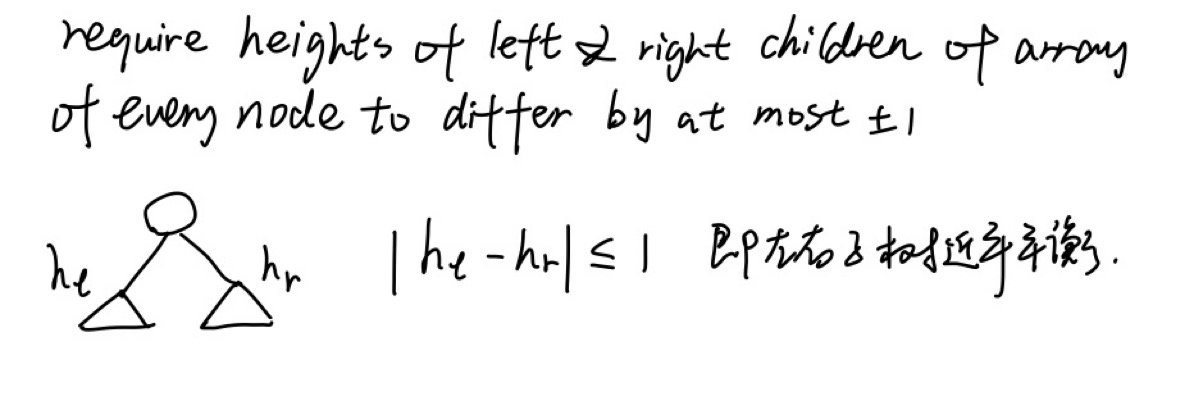
但有时会出现很糟糕的情况：右子树高比左子树高多1.

假设AVL节点数量为N_h，那么由上图，可得N_h = n = 1 + N_h-1 + N_h-2。这个如果算下去（课程没给出具体过程），会得到N_h > F_h = φ^h/√5，其中F_h是斐波那契数列（数字1，1，2，3，5，8－构成了一个序列。这个数列前面相邻两项之和，构成了后一项），φ=1.618，最后可以通过下图的得到h小于1.44log₂n。

除了通过上述方法，还有种更简单的方法估算h的大小：

在该方法下得到的结果2log₂n不如1.44log₂n来的更为准确。

 三、AVL的插入

AVL的插入分两步走：

1. 简单的二分搜索树BST插入（simple BST insert）；
2. 从修改结点向上满足AVL属性，因为下面插入可能会影响上面的结果（Fix AVL property from changed node up）。

举个例子可能会更好的解释上面的步骤：

（注：蓝色箭头表明哪边子树比较重。）

上图我们给定了一个BST，然后按照BST插入的方法将23插入进去，我们会发现，29-26-23不符合AVL的属性。为了解决这个问题，AVL有个旋转Rotiation操作，如下图：

如果我们对29-26-23进行右旋转即可得到正确的AVL结构：

除了上面这种情况，如果出现下图这种插入55后的情况，可以使用双旋转操作（double/two rotation）：

那么现在我们来假设一个通用场景，总结下AVL的调整方法。

假设x是最低违背AVL的结点，然后right(x)（或x.right）更高。出现下面两种情况则可以参考下面的旋转方案：

四、AVL排序

1. 插入n个items - 每插入一个item要花费h时间，h在平衡树下为log₂n，因此n个items为Ο(nlog₂n) ；
2. in-order traversal 按顺序遍历输出 - Ο(n) 。

五、总结

对于插入、删除、最小化，使用Heap和AVL就可以了，但是如果要求next_larger和next_smaller得要平衡二分查找树，不过现实很难满足完全平衡，那么用AVL高度平衡树来做也行。