U137971 公司搬迁 - 并查集 奇偶性

题目描述

因为人员规模扩大，T公司准备搬到新的写字楼去，写字楼分为A座和B座，n名不同工号的员工x（p1,p2,p3...pn） 按照下面两个规则确定在A座或者B座进行办公：
（1）如果工号为x的员工在A座，那么工号为a-x的员工肯定也在A座（编号为a-x的员工要保证存在，否则不成立）
（2）如果工号为x的员工在B座，那么工号为b-x的员工肯定也在B座（编号为b-x的员工要保证存在，否则不成立）
判断一下是否存在一种方案来分配所有员工的办公地点。如果能够分配全员的办公地点，输出YES；若存在至少一名 员工，找不到规则中与之对应的员工，输出NO。

注意：如果所有员工都在A座或者都在B座也可以。

 

输入格式

第一行输入一个T(1≤T≤10)，表示下面有多少组测试数据 对于每组测试数据的2行输入：
第1行有3个整数n,a,b (1≤n≤1e5; 1≤a,b≤1e9) 。 第2行有n个不一样的整数 p1,p2,...,pn (1≤pi≤1e9).

输出格式

每组数据输出一行结果，如果可行，那么输出YES，否则输出NO。

输入输出样例

输入 #1 复制

2
4 5 9
2 3 4 5
3 2 3
1 2 3

输出 #1 复制

YES
NO

输入 #2 复制

2
5 10 11
2 8 3 7 5
3 5 12
1 4 3

输出 #2 复制

YES
NO

说明/提示

数据范围

对于50%的数据，1 ≤ n ≤ 10，1 ≤ pi ≤ 20
对于65%的数据，1 ≤ n ≤ 100
对于100%的数据，1 ≤ n ≤ 1e5，1≤a,b≤1e9，1 ≤ pi ≤ 1e9，1≤T≤10

样例解释

对于样例1：
第一组数据中，四名员工的工号依次为{2,3,4,5}，此时a=5,b=9，可以安排{2,3}在A座，{4,5}在B座，人员分配完 成，该方案可行，所以第一行输出YES。
第二组数据中，无论如何工号为3的员工也无法找到与之对应的员工进行分配，所以第二行输出NO。

对于样例2：
第一组数据中，五名员工的工号依次为{2,3,7,8,5}，此时a=10,b=11，首先将5号员工安排在A座中，他与他自身对 应，符合题意；之后将{2,8}{3,7}分别也安排在A座，分配完成，输出YES。
第二组数据中，无论如何工号为3的员工也无法找到与之对应的员工进行分配，所以输出NO。

题解

　这题可以用2-sat做，然而我并不会，题解的做法开2倍并查集还看不懂，所以就自己乱搞。

　1.题意

　　其实就是给一些节点染色， 给定一些限制，要求某两个节点必须染成同一个颜色， 问是否存在可行方案。

　　有些细节就是，不能把某个点单独染成一个颜色，除非a-x = x， 即自环(见题目及样例)

　2.推性质

　　这题的关键部分就是推性质

　　　　1.建图后必然是许多条链

　　　　把a-x与b-x的限制看作边，则每个节点的度数最多为2，所以连接出来的一定是若干(因为不保证联通)条链。（如果首尾相连，也就是环，当做链就好了。读者可自己思考， 因为只有偶链可构成环，破环成链后奇偶性不变， 所以没必要）

　　　　2.一条链上的边必然是ABABAB..或BABABA...

　　　　称a-x为A边，b-x为B，因为连接某个节点的两条边必然不同，左边的如果是A，右边就是B.

　　　　3.同一条链上的所有节点颜色必然相同

　　　　假设有这样一条链

　　　　

　　　　假如把第一个染成A, 第二个点由于限制也是A

　　       

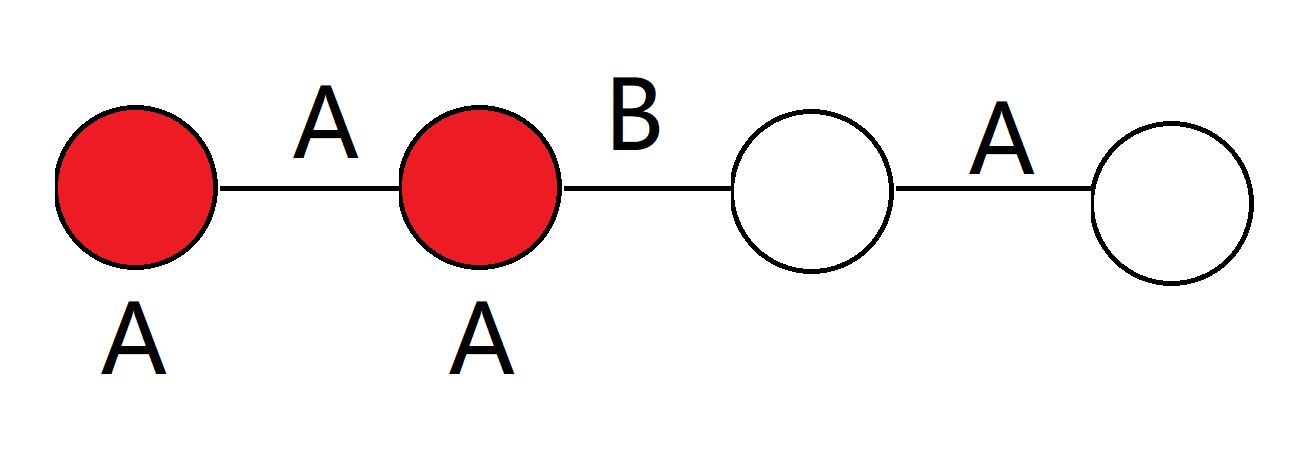
　　　　容易发现如果第三个点是B, 第二个点也应该是B,不成立

　　　　故第三个点也是A, 因为限制第四个点................

　　　　其他情况同理

　　　　

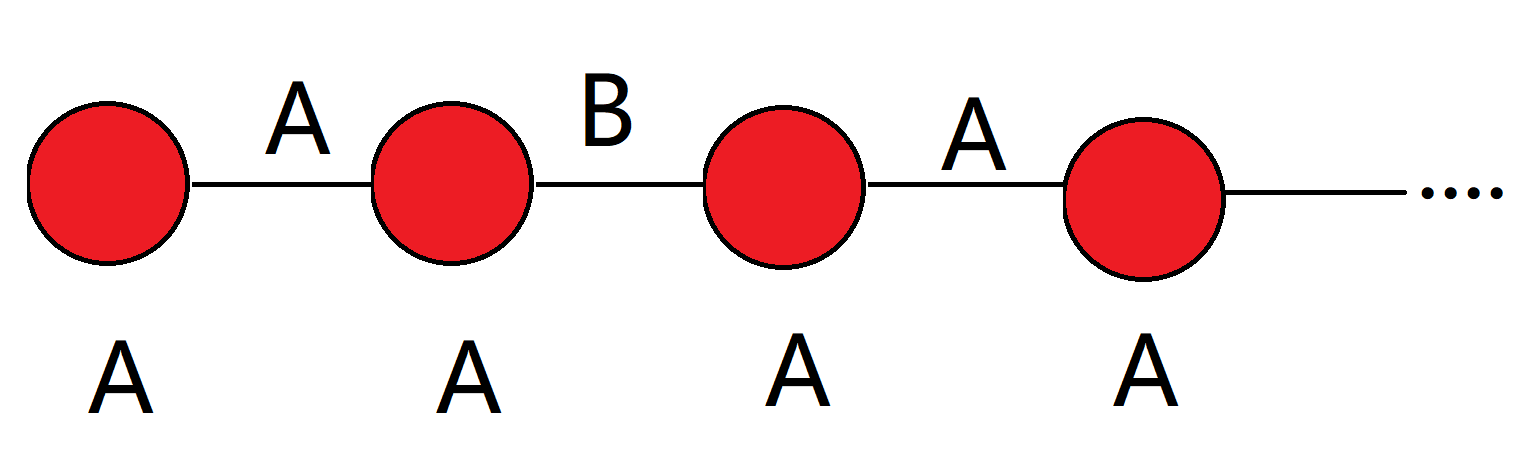
　　　　4.节点个数为偶数必然有解，奇数必无解

　　　　这就是关键了，假如有个图还是这样（节点是偶数个）

　　　　

　　　　容易发现全部染成A是合法的，将节点按顺序分成一对一对的，每队节点都以同一种类型的边相连， 并且没有剩下的（BABA形式也是同理）。

　　　　

　　　　进一步发现，奇数点无论怎么分都会剩下一个。

　　3.解题

　　　　显然只要维护每一条链的长度，判断奇偶性即可。

　　　　容易想到并查集来维护是否在同一条链即可, 顺便记录大小即可，并不需要开2倍。这样你就可以拿到75分的好成绩， 调了半天才发现一开始说的自环判错了，看这个图

　　　　

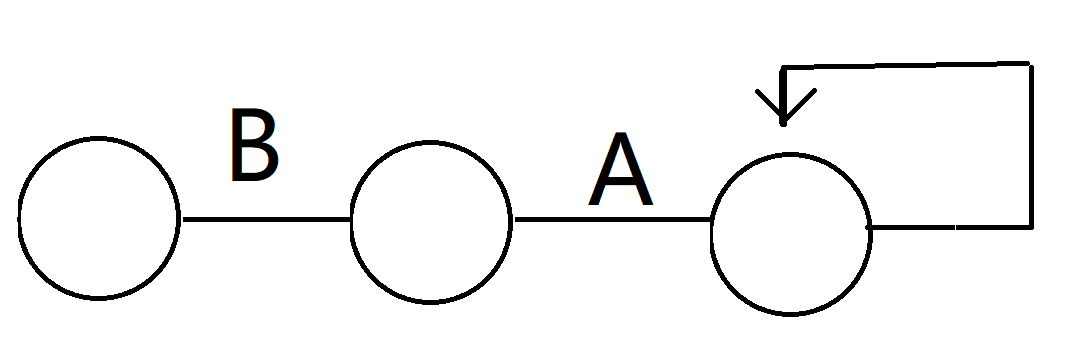
　　　　直接维护节点个数的话是3个，无解。但我并不是怎么干的（因为样例卡了），我把自环拆成两个节点

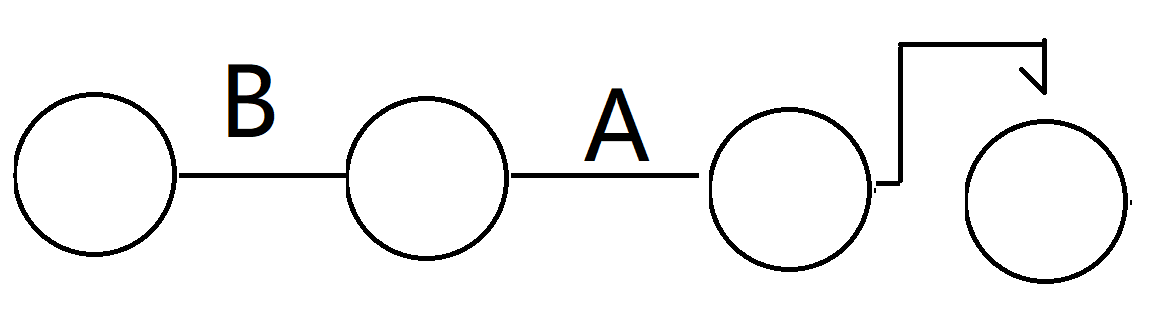　　　　好，判断成功了，样例全过了

　　　　这就是75分做法，再看个反例

　　　　

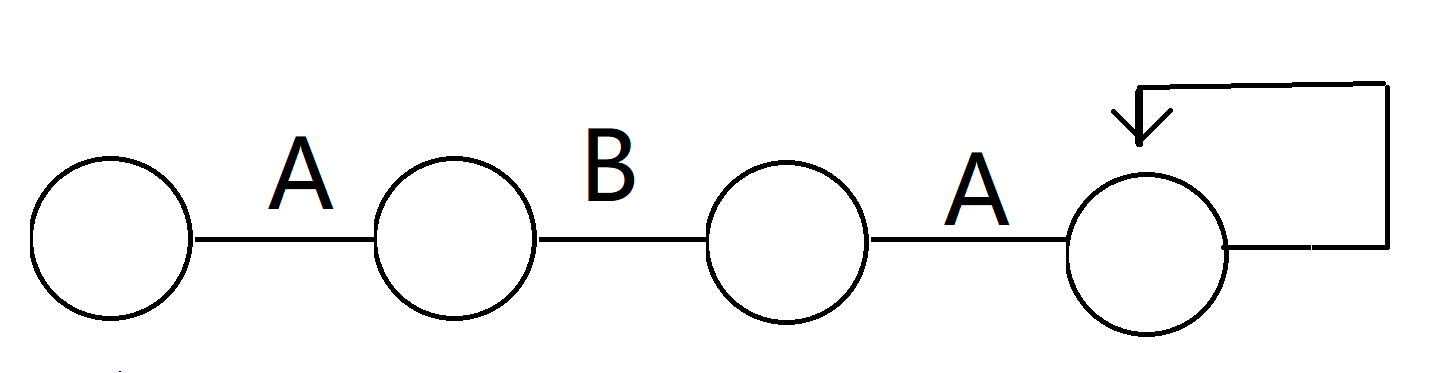
　　　　显然是可行的，但是把自环拆开后，节点个数加一，判断错误。

　　　　等等， 有没有发现什么：不管是奇数还是偶数，包含自环肯定有解。 因为自环既可以当做一个点，也可以自己和自己组一队，如果原链是奇链，则把自环剩下和自己匹配， 偶链忽略即可。 （并且自环只能出现在链尾，否则度数就超过3了。）

　　　　

　　　　总结： 维护链的奇偶性，存在自环则特判为偶链即可。

　　　　顺带一提：样例是错的，题目保证了数据互不相同， 代码做了去重，故可过样例。

　　　　

　　　　考试代码，太丑不想改了，抱歉

　　　　

#include <iostream>
#include <cstdio>
#include <algorithm>

#define N 300005
#define inf -1*0x3f3f3f3f

using namespace std;

int t, n, a, b, s[N], bc[N], bs[N];

int read(){
	int num=0; char c=getchar();
	while(c<'0' || c>'9') c=getchar();
	while(c>='0' && c<='9') num = num*10 + c-'0', c=getchar();
	return num;
} 

void build(){
	for(int i=1; i<=n; i++) bs[i]=1, bc[i]=i;
}

int find(int x){
	if(bc[x]==x) return x;
	return bc[x]=find(bc[x]);
} 

void link(int x1, int x2){
	int g1 = find(x1), g2=find(x2);
	bs[g1] += bs[g2];
	bc[g2] = g1;
}

int main(){
	t=read();
	while(t--){
		n=read(), a=read(), b=read();
		for(int i=1; i<=n; i++) s[i] = read();
		build();

		sort(s+1, s+1+n);

		for(int i=1; i<=n; i++){
			if(s[i]==s[i-1])continue;
			if(a>s[i]){
				if(a-s[i]==s[i]){
					bs[find(i)]=inf;
				}else{
					int nex = lower_bound(s+1, s+1+n, a-s[i])-s;
					if(s[nex] == a-s[i]){
						if(find(i) != find(nex)){
							link(i, nex);
						}
					}
				}
			}
			if(b>s[i]){
				if(b-s[i]==s[i]){
					bs[find(i)]=inf;
				}else {
					int nex = lower_bound(s+1, s+1+n, b-s[i])-s;
					if(s[nex] == b-s[i]){
						if(find(i) != find(nex)){
							link(i, nex);
						}
					}
				}
			}
		}
		int flag=true;
		for(int i=1; i<=n; i++){
			if(s[i]==s[i-1])continue;
			if(bs[find(i)] % 2 && bs[find(i)]>0){
				printf("NO\n");
				flag=false;
				break;
			}
		}
		if(flag) printf("YES\n");
	}

	return 0;
}

　　

　　多模拟样例，好题样例都会有所启发