学习笔记:[算法分析]数据结构与算法Python版[基本的数据结构-上]

线性结构Linear Structure

❖线性结构是一种有序数据项的集合，其中 每个数据项都有唯一的前驱和后继

　　除了第一个没有前驱，最后一个没有后继 新的数据项加入到数据集中时，只会加入到原有 某个数据项之前或之后 具有这种性质的数据集，就称为线性结构

 ❖线性结构总有两端，在不同的情况下，两 端的称呼也不同

　　有时候称为“左”“右”端、“前”“后”端、 “顶”“底”端

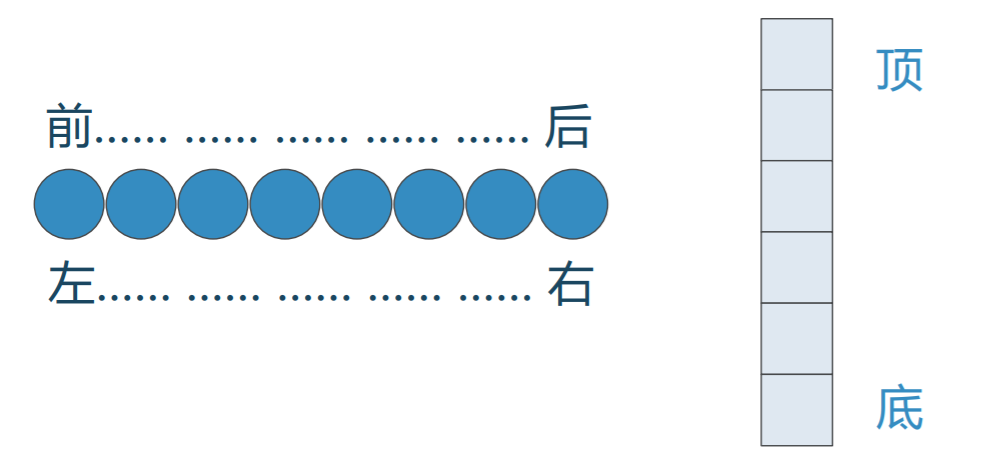
 ❖两端的称呼并不是关键，不同线性结构的 关键区别在于数据项增减的方式

　　 有的结构只允许数据项从一端添加，而有的结构 则允许数据项从两端移除

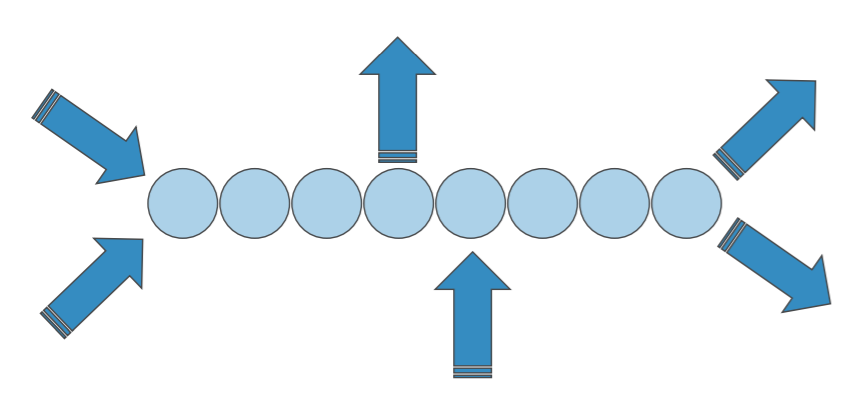
 ❖4个最简单但功能强大的结构:栈Stack，队列Queue，双端队列Deque 和列表List

　　这些数据集的共同点在于，数据项之间只存在先 后的次序关系，都是线性结构

 ❖这些线性结构是应用最广泛的数据结构 ,它们出现在各种算法中，用来解决大量重 要问题

、、、

什么是栈Stack

1.栈

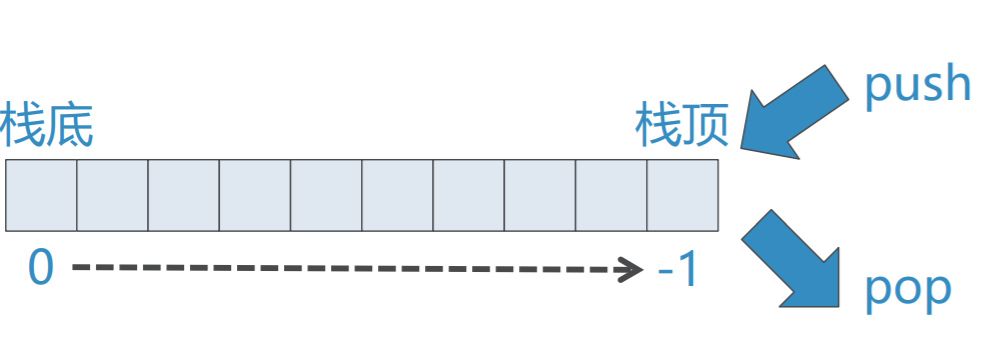
❖一种有次序的数据项集合，在栈中，数据 项的加入和移除都仅发生在同一端

　　这一端叫栈“顶top”，另一端叫栈“底base”

❖日常生活中有很多栈的应用

　　盘子、托盘、书堆等等

❖距离栈底越近的数据项，留在栈中的时间 就越长

　　而最新加入栈的数据项会被最先移除

❖这种次序通常称为“后进先出LIFO”： Last in First out

　　这是一种基于数据项保存时间的次序，时间越短 的离栈顶越近，而时间越长的离栈底越近

2.栈的特性：反转次序

❖我们观察一个由混合的python原生数据 对象形成的栈

　　进栈和出栈的次序正好相反

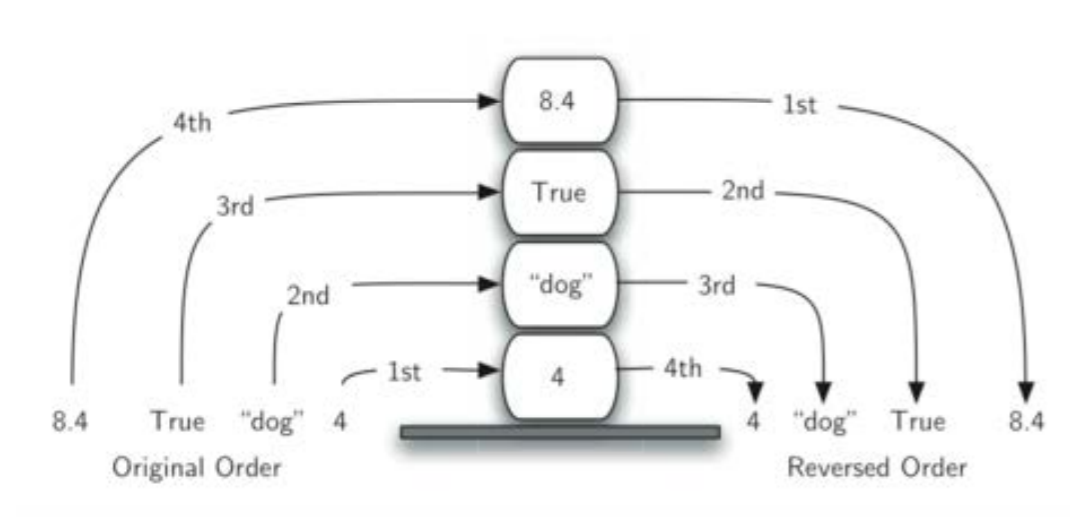
 ❖这种访问次序反转的特性，我们在某些计 算机操作上碰到过

　　浏览器的“后退back”按钮，最先back的是最 近访问的网页 Word的“Undo”按钮，最先撤销的是最近操作

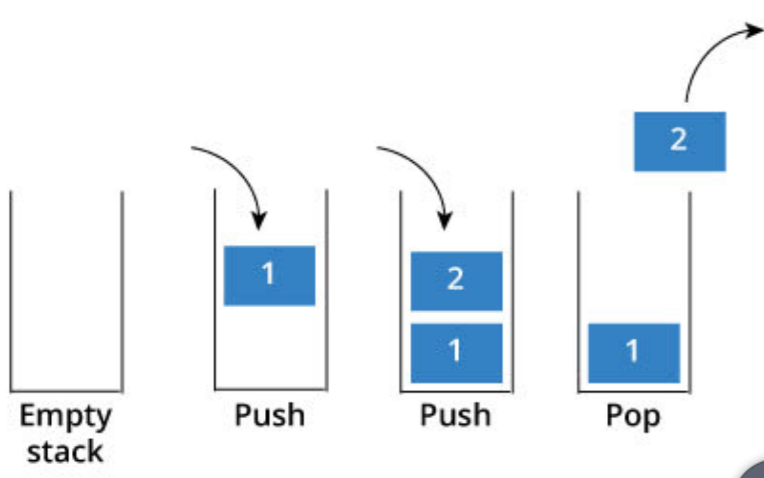
3.抽象数据类型Stack

❖抽象数据类型“栈”是一个有次序的数据 集，每个数据项仅从“栈顶”一端加入到 数据集中、从数据集中移除，栈具有后进 先出LIFO的特性

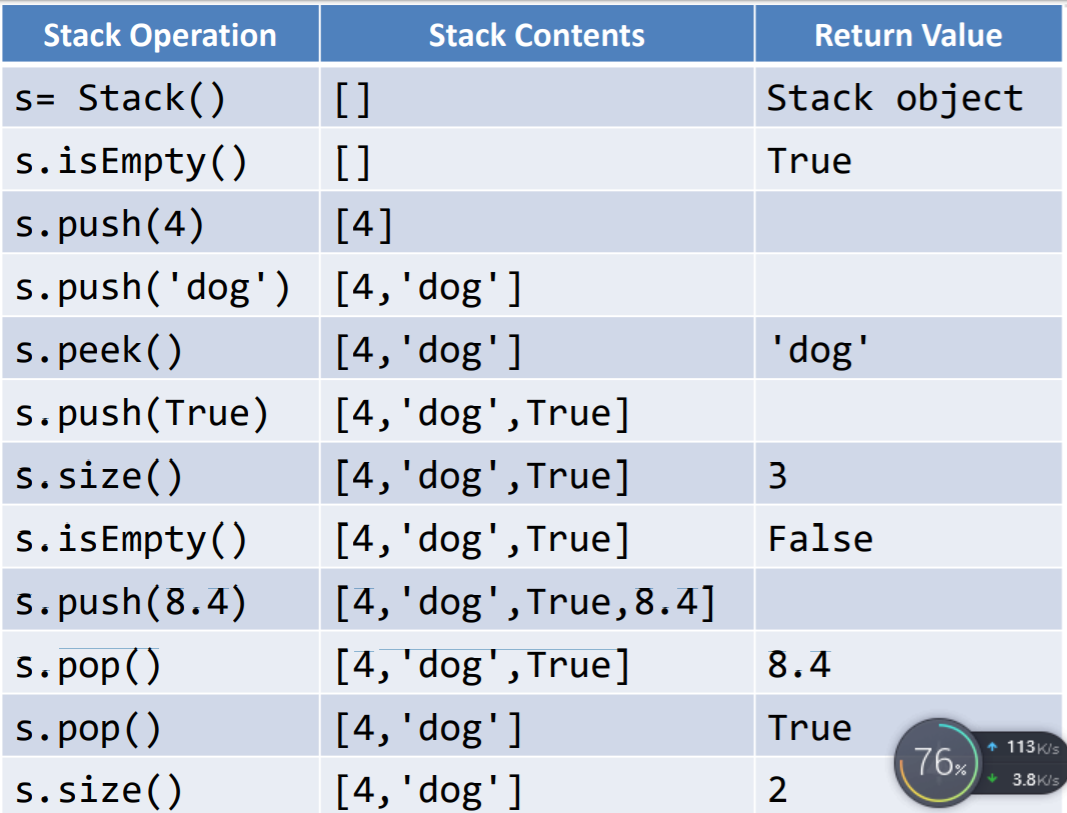
 ❖抽象数据类型“栈”定义为如下的操作

Stack()：创建一个空栈，不包含任何数据项

push(item)：将item加入栈顶，无返回值

pop()：将栈顶数据项移除，并返回，栈被修改

peek()：“窥视”栈顶数据项，返回栈顶的数 据项但不移除，栈不被修改

isEmpty()：返回栈是否为空栈

size()：返回栈中有多少个数据项

class Stack:
    def __init__(self):
        self.items=[]

    def isEmpty(self):
        return self.items==[]
    def push(self,item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()
    def peek(self):
        return self.items[len(self.items)-1]
    def size(self):
        return len(self.items)

s=Stack()

print(s.isEmpty())
s.push(4)
s.push('DOG')
print(s.peek())
s.push(True)
print(s.size())
print(s.isEmpty())
s.push(8.4)
print(s.pop())
print(s.pop())
print(s.size())

4.用Python实现ADT Stack

❖一个细节：Stack的两端对应list设置

可以将List的任意一端（index=0或者-1）设置 为栈顶 我们选用List的末端（index=-1）作为栈顶 这样栈的操作就可以通过对list的append和pop 来实现，很简单！

代码:

class Stack:
    def __init__(self):
        self.items=[]
    def isEmpty(self):
        return self.items==[]
    def push(self,item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()
    def peek(self):
        return self.items[len(self.items)-1]
    def size(self):
        return len(self.items)

5.ADT Stack的另一个实现

❖不同的实现方案保持了ADT接口的稳定性

　　但性能有所不同，栈顶首端的版本（左），其 push/pop的复杂度为O(n)，而栈顶尾端的实现 （右），其push/pop的复杂度为O(1)

栈的应用：简单括号匹配

1.简单括号匹配

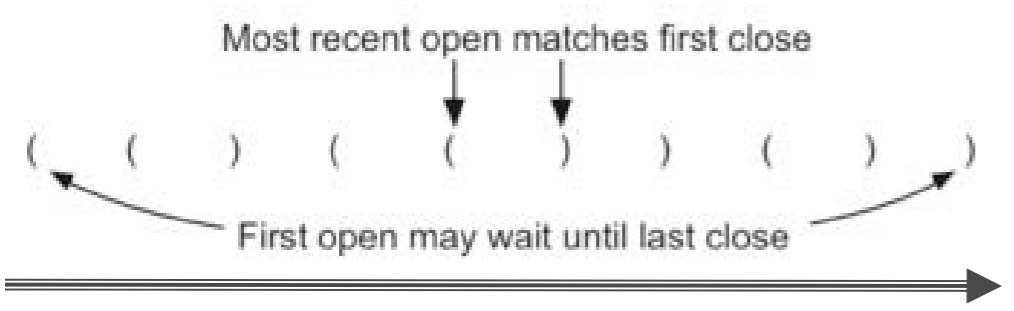
❖如何构造括号匹配识别算法

从左到右扫描括号串，最新打开的左括号，应该 匹配最先遇到的右括号 这样，第一个左括号（最早打开），就应该匹配 最后一个右括号（最后遇到） 这种次序反转的识别，正好符合栈的特性

最终代码:

class Stack:
    def __init__(self):
        self.items=[]

    def isEmpty(self):
        return self.items==[]
    def push(self,item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()
    def peek(self):
        return self.items[len(self.items)-1]
    def size(self):
        return len(self.items)

def parChecker(symbolString):
    s=Stack()
    balanced=True
    index=0

#    判断是否大于传进来参数的长循环次数度 与 balanced变量是否为真
#    如果达到这两个条件终止循环
    while index<len(symbolString) and balanced:
        symbol=symbolString[index]
        #判断当前传进来的第index个字符是不是等于"C"
        if symbol=="(":
            #如果是push进栈
            s.push(symbol)
        else:
            #否则判断栈是否为空
            if s.isEmpty():
                blanced=False
            else:
                #如果不空则将数据pop出去
                s.pop()
        index=index+1

    #balanced必须为true 数组还要为空 则true
    if balanced and s.isEmpty():
        return True
    else:
        return False

print(parChecker('(())'));
print(parChecker('(()'));
        

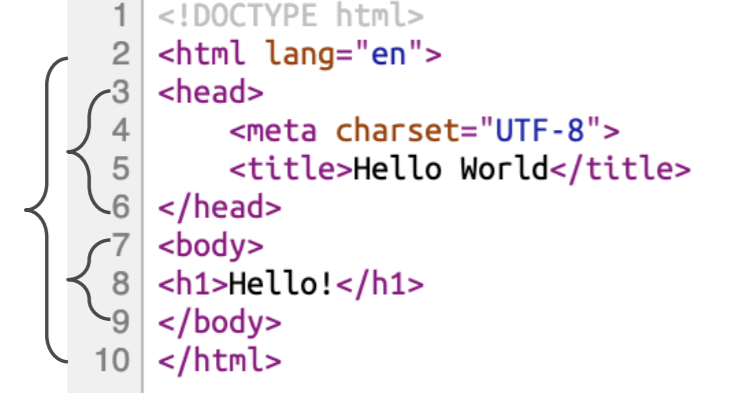
2.通用括号匹配

❖HTML/XML文档也有类似于括号的开闭 标记，这种层次结构化文档的校验、操作 也可以通过栈来实现

栈的应用：十进制转换为二进制

1.二进制转十进制

❖ 二进制是计算机原理中最基本的概念，作为组成 计算机最基本部件的逻辑门电路，其输入和输出 均仅为两种状态：0和1

❖ 但十进制是人类传统文化中最基本的数值概念， 如果没有进制之间的转换，人们跟计算机的交互 会相当的困难

❖所谓的“进制” ，就是用多少个字符来表 示整数

　　十进制是0～9这十个数字字符，二进制是0、1两 个字符

❖十进制转换为二进制，采用的是“除以2 求余数”的算法 将整数不断除以2，每次得到的余数就是由低到 高的二进制位

❖“除以2”的过程，得到的余数是从低到 高的次序，而输出则是从高到低，所以需 要一个栈来反转次序

 十进制转二进制代码:

class Stack:
    def __init__(self):
        self.items=[]

    def isEmpty(self):
        return self.items==[]
    def push(self,item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()
    def peek(self):
        return self.items[len(self.items)-1]
    def size(self):
        return len(self.items)

def divideBy2(decNumber):
  remstack=Stack()

  while decNumber>0:
      rem=decNumber%2
      remstack.push(rem)
      decNumber=decNumber // 2

  binString=""
  while not remstack.isEmpty():
      binString=binString+str(remstack.pop())
  return binString;

print(divideBy2(42));

2.扩展到更多进制转换

❖十进制转换为二进制的算法，很容易可以 扩展为转换到任意N进制

　　只需要将“除以2求余数”算法改为“除以N求余 数”算法就可以

❖计算机中另外两种常用的进制是八进制和 十六进制

❖主要的问题是如何表示八进制及十六进制

二进制有两个不同数字0、1

十进制有十个不同数字0、1、2、3、4、5、6、 7、8、9

八进制可用八个不同数字0、1、2、3、4、5、6 、7

十六进制的十六个不同数字则是0、1、2、3、4 、5、6、7、8、9、A、B、C、D、E、F

扩展到多进制代码:

class Stack:
    def __init__(self):
        self.items=[]

    def isEmpty(self):
        return self.items==[]
    def push(self,item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()
    def peek(self):
        return self.items[len(self.items)-1]
    def size(self):
        return len(self.items)

def divideBy2(decNumber,base):
  digits="0123456789ABCDEF"
  remstack=Stack()

  while decNumber>0:
      rem=decNumber%base
      remstack.push(rem)
      decNumber=decNumber // base

  binString=""
  while not remstack.isEmpty():
      binString=binString+digits[remstack.pop()]
  return binString;

print(divideBy2(25,2));
print(divideBy2(25,16));

什么是算法分析

11

什么是算法分析

111