论文解读（g-U-Nets）《Graph U-Nets》

论文信息

论文标题：Graph U-Nets
论文作者：Hongyang Gao, Shuiwang Ji
论文来源：2019,ICML
论文地址：download 
论文代码：download

1 Introduction

　　受到类似 encoder-decoder architecture 的 U-Nets 影响，作者希望能在图数据上使用这种 pooling 和 up-sampling 的操作。

　　Note：Encoder 一般是降维，可以看成 pooling ；而 Decoder 一般是升维，可以看成 up-sampling 操作。

2 Graph U-Nets

　　本节依次介绍 graph pooling (gPool) layer， graph unpooling (gUnpool) layer，然后介绍本文用于节点分类的 U-Nets 。

2.1 Graph Pooling Layer

　　global pooling 操作将把所有节点减少为一个节点，这限制了网络的灵活性。k-max pooling 操作输出图中可能来自不同节点的 $k$ 个最大单元，导致所选节点的连通性不一致。

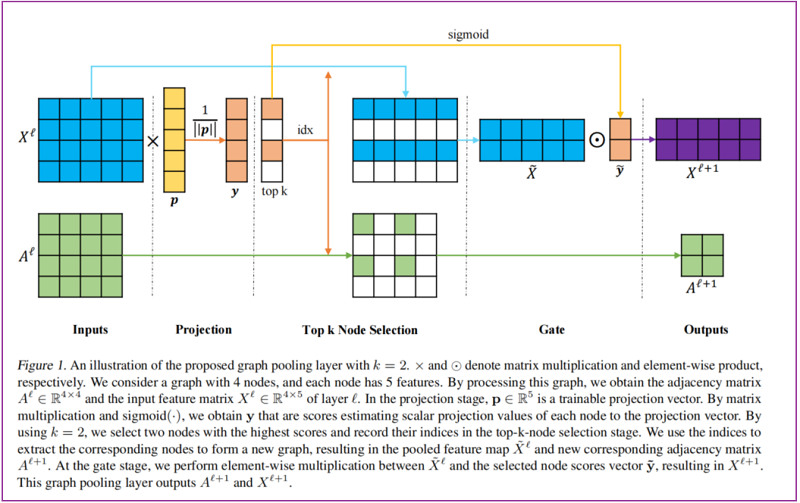
　　本文提出利用投影向量  $\mathbf{p}$  来计算图中各个节点的重要性，并且  $\mathbf{p}$  是可训练的参数，不需要认为指定。假设节点的嵌入向量为  $\mathbf{x}_{\mathrm{i}}$ , 它在向量  $\mathbf{p}$  上的投影为  $\mathrm{y}_{\mathrm{i}}=\mathbf{x}_{\mathrm{i}} \mathbf{p} /\|\mathbf{p}\|$， $\mathrm{y}_{\mathrm{i}}$  可以作为衡量节点重要性的度量。

　　$\mathrm{gPool}$ 计算过程为：

　　　　$\begin{array}{l}\mathbf{y} &=&X^{\ell} \mathbf{p}^{\ell} /\left\|\mathbf{p}^{\ell}\right\| \\\mathrm{idx} &=&\operatorname{rank}(\mathbf{y}, k) \\\tilde{\mathbf{y}} &=&\operatorname{sigmoid}(\mathbf{y}(\mathrm{idx})) \\\tilde{X}^{\ell} &=&X^{\ell}(\mathrm{idx},:) \\A^{\ell+1} &=&A^{\ell}(\mathrm{idx}, \mathrm{idx}) \\X^{\ell+1} &=&\tilde{X}^{\ell} \odot\left(\tilde{\mathbf{y}} \mathbf{1}_{C}^{T}\right)\end{array}$

　　图示如下：

　　

2.2 Graph Unpooling Layer

　　为在图数据上实现 up-sampling 操作，本文提出 graph unpooling (gUnpool) layer。

　　

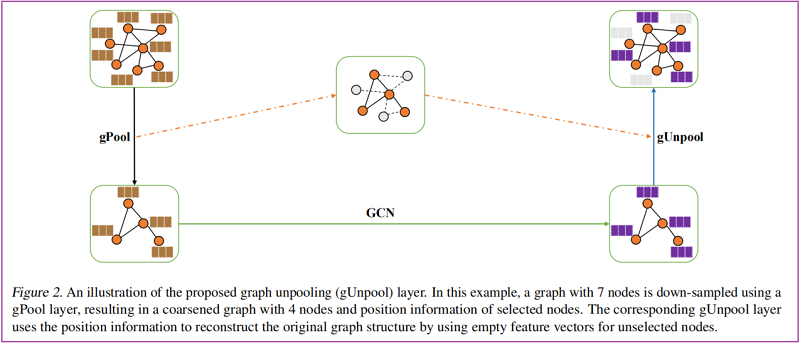
　　在形式上，gUnpool 的层级传播规则为：

　　　　$X^{\ell+1}=\operatorname{distribute}\left(0_{N \times C}, X^{\ell}, \mathrm{idx}\right)$

　　其中，

• • $idx \in \mathbb{Z}^{* k}$ 包含在相应的 gPool 层中所选节点的索引，从而将图的大小从 $N$ 个节点减少到 $k$ 个节点；
  • $X^{\ell} \in \mathbb{R}^{k \times C}$ 是当前图的特征矩阵；
  • $0_{N \times C}$ 是新图的 0 填充的特征矩阵；

　　Note：在 $X^{\ell+1}$ 中，$idx$ 中具有索引的行向量由 $X^{\ell}$ 中的行向量更新，而其他行向量保持为零。

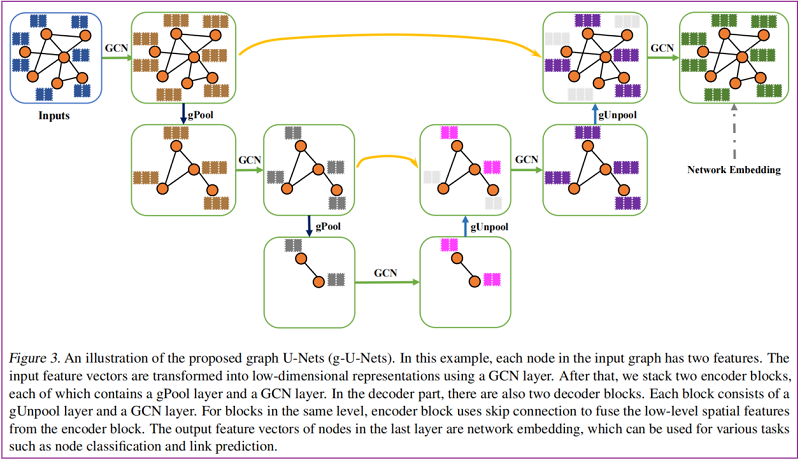
2.3 Graph U-Nets Architecture

　　如图所示：

　　

2.4 Graph Connectivity Augmentation via Graph Power

　　在 gPool 层中，对一些重要的节点进行采样，形成一个新的特征编码图。由于在删除 gPool 中的节点时相关边被删除，所以 pooled graph 中可能形成孤立点。可能会影响信息在后续层中的传播，特别是当使用 GCN 层来聚合来自邻近节点的信息时。所以需要增加 pooled graph 中节点之间的连通性。

　　为了解决上述问题，使用第 $k$ 个图的幂 $\mathbb{G}^{k}$ 来增加图的连通性。文中使用 $k = 2$ ，替换计算过程中的 $A^{\ell+1}$：

　　　　$A^{2}=A^{\ell} A^{\ell}, \quad A^{\ell+1}=A^{2}(\mathrm{idx}, \mathrm{idx})$

2.5 Improved GCN Layer

　　在  $\mathrm{GCN}$  中邻接矩阵  $\hat{\mathrm{A}}=\mathrm{A}+\mathrm{I}$ , 论文中改为  $\hat{\mathrm{A}}=\mathrm{A}+2 \mathrm{I}$，给予中心节点更大的权重。

3 Experimental Study

数据集

　　

　　

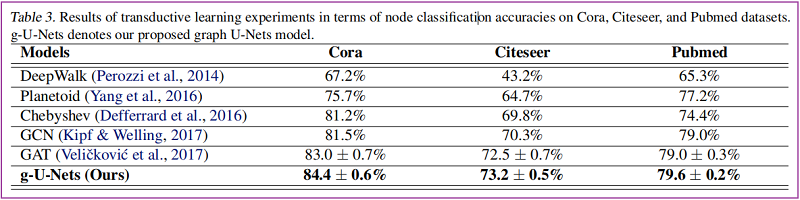
节点分类

　　

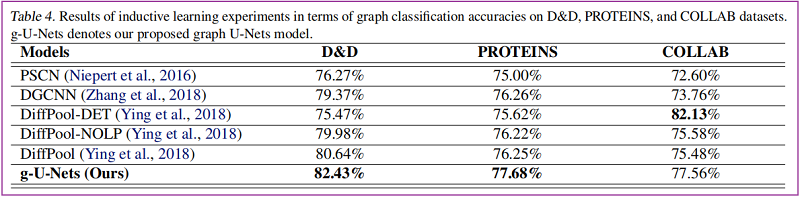
图分类

　　

4 Conclusion

　　在这项工作中，我们提出了g-U-Nets网络中新的 gPool 和 gUnpool 层用于网络嵌入。gPool 层对图形数据实现了规则的全局 k-max 池化操作。它对重要节点的子集进行采样，以实现高级特征编码和接受域扩大。通过使用一个可训练的投影向量，gPool层根据其标量投影值对节点进行采样。此外，我们提出了对图数据应用非池操作的gUnpool层。利用原图中节点的位置信息，gUnpool 层对相应的 gPool 层进行逆操作，恢复原图的结构。基于我们的 gPool 和 gUnpool 层，我们提出了图 U-Nets(gU-Nets) 结构，它在图像数据上使用与常规U-Net类似的编码-解码器结构。实验结果表明，与其他gnn相比，我们的g-u-net在转换学习任务上实现了性能的提高。为了避免采样图中可能存在的孤立节点问题，我们采用第二图幂来提高图的连通性。对消融术的研究表明了这些贡献