2023-01-12：一个n*n的二维数组中，只有0和1两种值， 当你决定在某个位置操作一次， 那么该位置的行和列整体都会变成1，不管之前是什么状态。 返回让所有值全变成1，最少的操作次数。 1 ＜

2023-01-12：一个n*n的二维数组中，只有0和1两种值，
当你决定在某个位置操作一次，
那么该位置的行和列整体都会变成1，不管之前是什么状态。
返回让所有值全变成1，最少的操作次数。
1 < n < 10，没错！原题就是说n < 10, 不会到10！最多到9！
来自华为。

答案2023-01-12：

四维dp+贪心。这道题优化力度很有限，跟暴力差不多。
代码用rust和solidity编写。

代码用solidity编写。代码如下：

// SPDX-License-Identifier: MIT
pragma solidity ^0.8.17;

contract Hello{

    function main() public pure returns (int32){
		int32[][] memory matrix = new int32[][](2);
		for (int32 i = 0; i < 2; i++) {
            matrix[uint32(i)] = new int32[](2);
			for (int32 j = 0; j < 2; j++) {
				matrix[uint32(i)][uint32(j)] = 0;
			}
		}
        matrix[1][1] = 1;
		int32 ans = setOneMinTimes3(matrix);
		return ans;
    }

    // 正式方法 + 贪心
	function setOneMinTimes3(int32[][] memory matrix) public pure returns (int32) {
		int32 n = int32(uint32(matrix.length));
		int32 m = int32(uint32(matrix[0].length));
		int32[] memory arr = new int32[](uint32(n));
		for (int32 i = 0; i < n; i++) {
			int32 status = 0;
			for (int32 j = 0; j < m; j++) {
				if (matrix[uint32(i)][uint32(j)] == 1) {
					status |= leftk(j);
				}
			}
			arr[uint32(i)] = status;
		}
        int32[][][][] memory dp = new int32[][][][](uint32(leftk(n)));
		for (int32 a = 0; a < leftk(n); a++) {
            dp[uint32(a)] = new int32[][][](uint32(leftk(m)));
			for (int32 b = 0; b < leftk(m); b++) {
                dp[uint32(a)][uint32(b)] = new int32[][](uint32(n));
				for (int32 c = 0; c < n; c++) {
                    dp[uint32(a)][uint32(b)] [uint32(c)] = new int32[](uint32(m));
					for (int32 d = 0; d < m; d++) {
						dp[uint32(a)][uint32(b)] [uint32(c)][uint32(d)]  = -1;
					}
				}
			}
		}
		return process3(arr, n, m, 0, 0, 0, 0, dp);
	}

	function process3(int32[] memory arr, int32 n, int32 m, int32 row, int32 col, int32 r, int32 c, int32[][][][] memory dp) public pure returns (int32) {
		if (r == n) {
			for (int32 i = 0; i < n; i++) {
				if ((row & leftk(i)) == 0 && (arr[uint32(i)] | col) != leftk(m) - 1) {
					return 2147483647;
				}
			}
			return 0;
		}
		if (c == m) {
			return process3(arr, n, m, row, col, r + 1, 0, dp);
		}
		if (dp[uint32(row)][uint32(col)][uint32(r)][uint32(c)] != -1) {
			return dp[uint32(row)][uint32(col)][uint32(r)][uint32(c)];
		}
		int32 p1 = process3(arr, n, m, row, col, r, c + 1, dp);
		int32 p2 = 2147483647;
		int32 next2 = process3(arr, n, m, row | leftk(r), col | leftk(c), r + 1, 0, dp);
		if (next2 != 2147483647) {
			p2 = 1 + next2;
		}
		int32 ans = min(p1, p2);
		dp[uint32(row)][uint32(col)][uint32(r)][uint32(c)] = ans;
		return ans;
	}

	function leftk(int32 k) public pure returns (int32){
		int32 ans = 1;
		while (k>0){
			ans*=2;
			k--;
		}
		return ans;
	}

	function min(int32 a,int32 b)public pure returns (int32){
		if(a<b){
			return a;
		}else{
			return b;
		}
	}

}

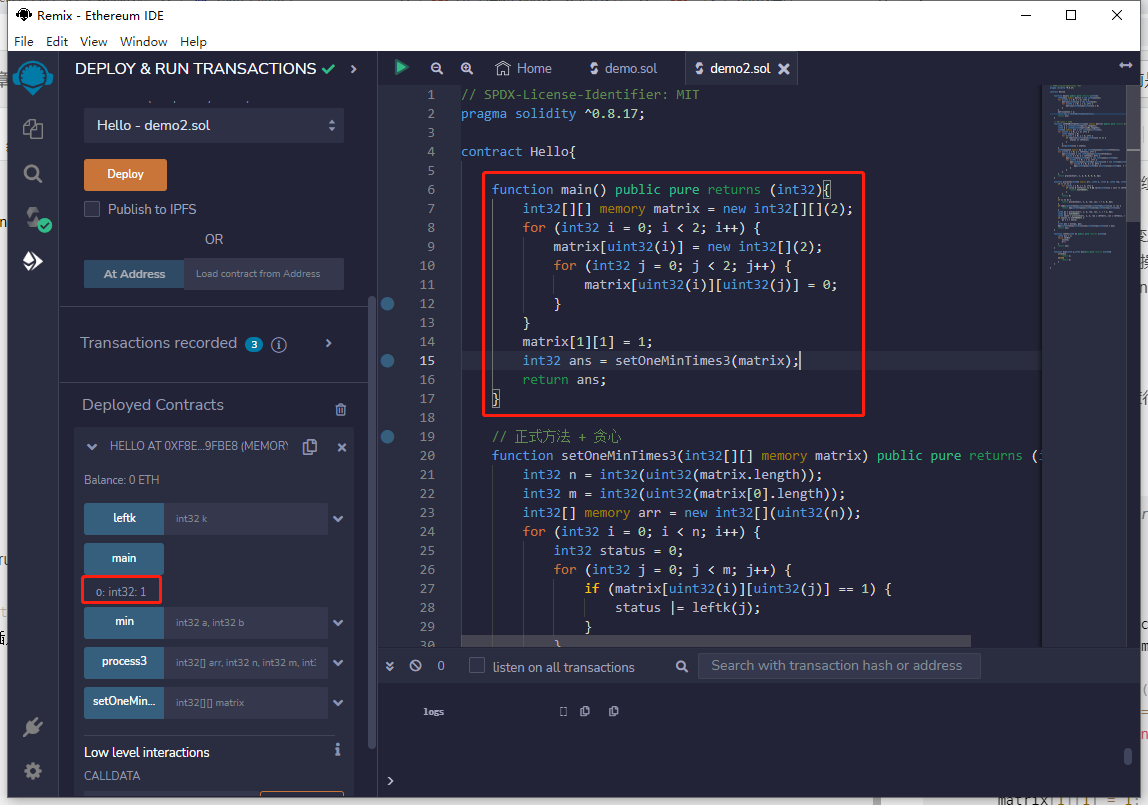
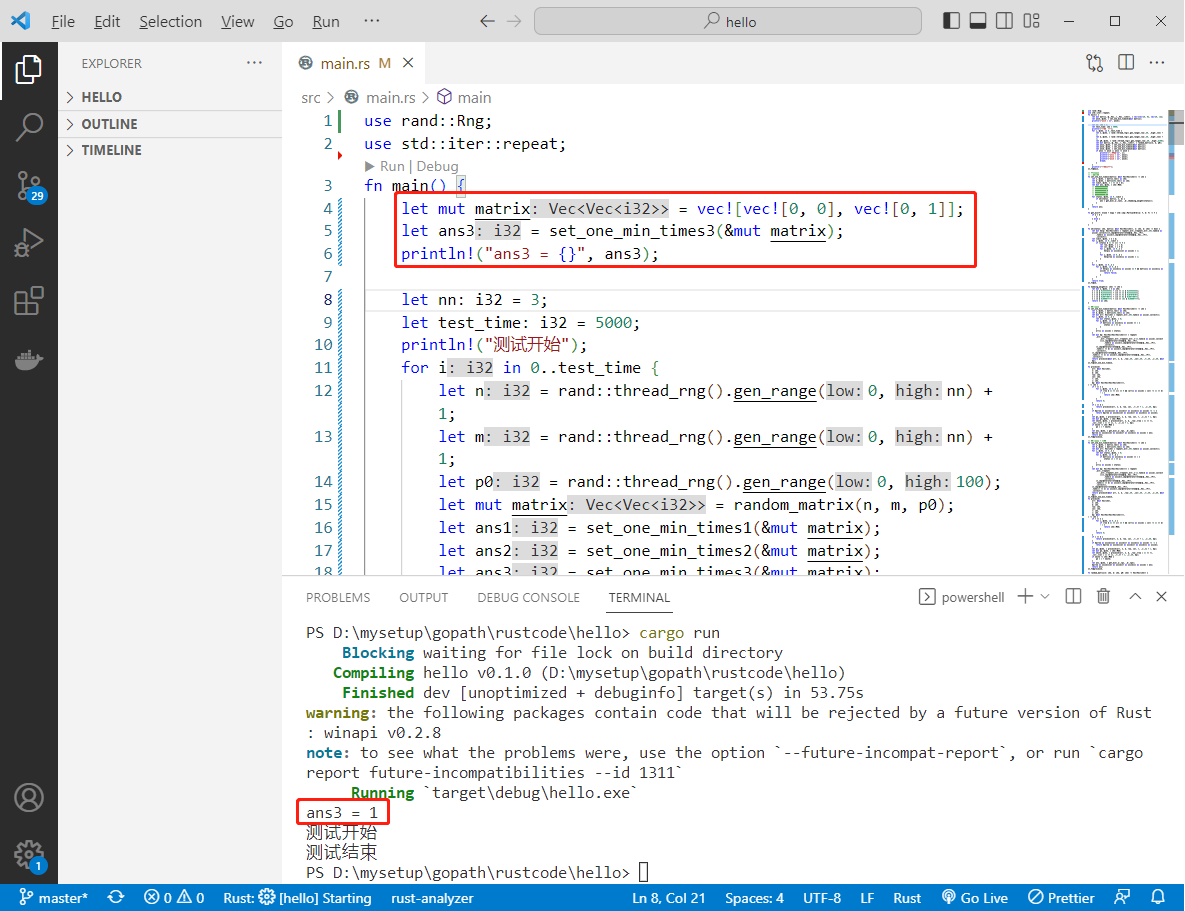
代码用rust编写。代码如下：

use rand::Rng;
use std::iter::repeat;
fn main() {
    let mut matrix = vec![vec![0, 0], vec![0, 1]];
    let ans3 = set_one_min_times3(&mut matrix);
    println!("ans3 = {}", ans3);

    let nn: i32 = 3;
    let test_time: i32 = 5000;
    println!("测试开始");
    for i in 0..test_time {
        let n = rand::thread_rng().gen_range(0, nn) + 1;
        let m = rand::thread_rng().gen_range(0, nn) + 1;
        let p0 = rand::thread_rng().gen_range(0, 100);
        let mut matrix = random_matrix(n, m, p0);
        let ans1 = set_one_min_times1(&mut matrix);
        let ans2 = set_one_min_times2(&mut matrix);
        let ans3 = set_one_min_times3(&mut matrix);
        if ans1 != ans2 || ans1 != ans3 {
            println!("出错了!{}", i);
            println!("ans1 = {}", ans1);
            println!("ans2 = {}", ans2);
            println!("ans3 = {}", ans3);
            break;
        }
    }
    println!("测试结束");
}

// 暴力方法
// 为了验证
fn set_one_min_times1(matrix: &mut Vec<Vec<i32>>) -> i32 {
    let n = matrix.len() as i32;
    let m = matrix[0].len() as i32;
    let limit = 1 << (n * m);
    let mut ans = i32::MAX;
    // 0000000000000
    // 0000000000001
    // 0000000000010
    // 0000000000011
    // 0000000000100
    for status in 0..limit {
        if ok(status, matrix, n, m) {
            ans = get_min(ans, hamming_weight(status));
        }
    }
    return ans;
}

fn get_min<T: Clone + Copy + std::cmp::PartialOrd>(a: T, b: T) -> T {
    if a < b {
        a
    } else {
        b
    }
}

fn ok(status: i32, matrix: &mut Vec<Vec<i32>>, n: i32, m: i32) -> bool {
    let mut help: Vec<Vec<i32>> = repeat(repeat(0).take(m as usize).collect())
        .take(n as usize)
        .collect();
    let limit = n * m;
    for i in 0..limit {
        if (status & (1 << i)) != 0 {
            let row = i / m;
            let col = i % m;
            for j in 0..n {
                help[j as usize][col as usize] = 1;
            }
            for j in 0..m {
                help[row as usize][j as usize] = 1;
            }
        }
    }
    for i in 0..n {
        for j in 0..m {
            if help[i as usize][j as usize] == 0 && matrix[i as usize][j as usize] == 0 {
                return false;
            }
        }
    }
    return true;
}

fn hamming_weight(n: i32) -> i32 {
    let mut n = n as u32;
    n = (n & 0x55555555) + ((n >> 1) & 0x55555555);
    n = (n & 0x33333333) + ((n >> 2) & 0x33333333);
    n = (n & 0x0f0f0f0f) + ((n >> 4) & 0x0f0f0f0f);
    n = (n & 0x00ff00ff) + ((n >> 8) & 0x00ff00ff);
    n = (n & 0x0000ffff) + ((n >> 16) & 0x0000ffff);
    return n as i32;
}

// 正式方法
fn set_one_min_times2(matrix: &mut Vec<Vec<i32>>) -> i32 {
    let n = matrix.len() as i32;
    let m = matrix[0].len() as i32;
    let mut arr: Vec<i32> = repeat(0).take(n as usize).collect();
    for i in 0..n {
        let mut status = 0;
        for j in 0..m {
            if matrix[i as usize][j as usize] == 1 {
                status |= 1 << j;
            }
        }
        arr[i as usize] = status;
    }
    let mut dp: Vec<Vec<Vec<Vec<i32>>>> = repeat(
        repeat(
            repeat(repeat(-1).take(m as usize).collect())
                .take(n as usize)
                .collect(),
        )
        .take((1 << m) as usize)
        .collect(),
    )
    .take((1 << n) as usize)
    .collect();
    return process2(&mut arr, n, m, 0, 0, 0, 0, &mut dp);
}

fn process2(
    arr: &mut Vec<i32>,
    n: i32,
    m: i32,
    row: i32,
    col: i32,
    r: i32,
    c: i32,
    dp: &mut Vec<Vec<Vec<Vec<i32>>>>,
) -> i32 {
    if r == n {
        for i in 0..n {
            if (row & (1 << i)) == 0 && (arr[i as usize] | col) != (1 << m) - 1 {
                return i32::MAX;
            }
        }
        return 0;
    }
    if c == m {
        return process2(arr, n, m, row, col, r + 1, 0, dp);
    }
    if dp[row as usize][col as usize][r as usize][c as usize] != -1 {
        return dp[row as usize][col as usize][r as usize][c as usize];
    }
    let p1 = process2(arr, n, m, row, col, r, c + 1, dp);
    let mut p2 = i32::MAX;
    let next2 = process2(arr, n, m, row | (1 << r), col | (1 << c), r, c + 1, dp);
    if next2 != i32::MAX {
        p2 = 1 + next2;
    }
    let ans = get_min(p1, p2);
    dp[row as usize][col as usize][r as usize][c as usize] = ans;
    return ans;
}

// 正式方法 + 贪心
fn set_one_min_times3(matrix: &mut Vec<Vec<i32>>) -> i32 {
    let n = matrix.len() as i32;
    let m = matrix[0].len() as i32;
    let mut arr: Vec<i32> = repeat(0).take(n as usize).collect();
    for i in 0..n {
        let mut status = 0;
        for j in 0..m {
            if matrix[i as usize][j as usize] == 1 {
                status |= 1 << j;
            }
        }
        arr[i as usize] = status;
    }
    let mut dp: Vec<Vec<Vec<Vec<i32>>>> = repeat(
        repeat(
            repeat(repeat(-1).take(m as usize).collect())
                .take(n as usize)
                .collect(),
        )
        .take((1 << m) as usize)
        .collect(),
    )
    .take((1 << n) as usize)
    .collect();
    return process3(&mut arr, n, m, 0, 0, 0, 0, &mut dp);
}
fn process3(
    arr: &mut Vec<i32>,
    n: i32,
    m: i32,
    row: i32,
    col: i32,
    r: i32,
    c: i32,
    dp: &mut Vec<Vec<Vec<Vec<i32>>>>,
) -> i32 {
    if r == n {
        for i in 0..n {
            if (row & (1 << i)) == 0 && (arr[i as usize] | col) != (1 << m) - 1 {
                return i32::MAX;
            }
        }
        return 0;
    }
    if c == m {
        return process3(arr, n, m, row, col, r + 1, 0, dp);
    }
    if dp[row as usize][col as usize][r as usize][c as usize] != -1 {
        return dp[row as usize][col as usize][r as usize][c as usize];
    }
    let p1 = process3(arr, n, m, row, col, r, c + 1, dp);
    let mut p2 = i32::MAX;
    let next2 = process3(arr, n, m, row | (1 << r), col | (1 << c), r + 1, 0, dp);
    if next2 != i32::MAX {
        p2 = 1 + next2;
    }
    let ans = get_min(p1, p2);
    dp[row as usize][col as usize][r as usize][c as usize] = ans;
    return ans;
}

fn random_matrix(n: i32, m: i32, p0: i32) -> Vec<Vec<i32>> {
    let mut ans: Vec<Vec<i32>> = repeat(repeat(0).take(m as usize).collect())
        .take(n as usize)
        .collect();
    for i in 0..n {
        for j in 0..m {
            ans[i as usize][j as usize] = if rand::thread_rng().gen_range(0, 100) < p0 {
                0
            } else {
                1
            };
        }
    }
    return ans;
}