Python数据分析--Numpy常用函数介绍(9)--Numpy中几中常见的图形

在NumPy中，所有的标准三角函数如sin、cos、tan等均有对应的通用函数。

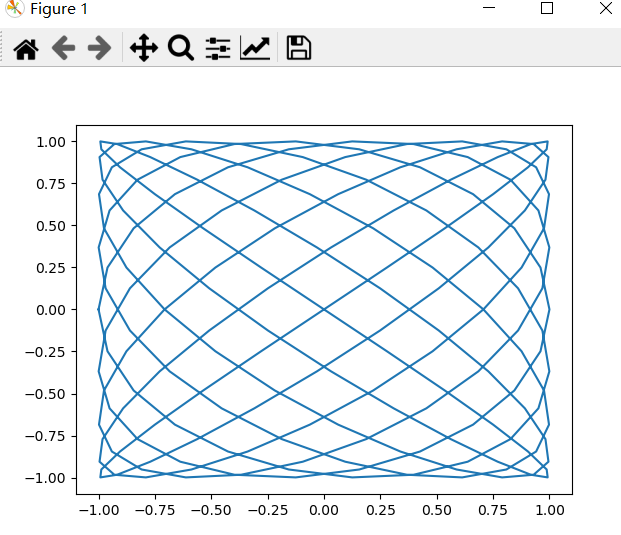
一、利萨茹曲线

（Lissajous curve）利萨茹曲线是一种很有趣的使用三角函数的方式(示波器上显示出利萨茹曲线)。利萨茹曲线由以下参数方程定义：

x = A sin(at + n/2)

y = B sin(bt)
利萨茹曲线的参数包括 A 、 B 、 a 和 b 。为简单起见，我们令 A 和 B 均为1,设置的参数为 a=9 ， b=8

import numpy as np
import matplotlib.pyplot as plt

A=B=1
a=9
b=8

t = np.linspace(-np.pi, np.pi, 201)  #使用linspace函数初始化变量t
x = np.sin(a * t + np.pi/2)  # sin 函数和NumPy常量 pi 计算变量 x
y = np.sin(b * t)  # sin函数计算变量y
plt.plot(x, y)
plt.show()

运行结果：

二、计算斐波那契数列

斐波那契数列的递推关系可以用矩阵来表示。斐波那契数列的计算等价于矩阵的连乘。可用两种方法计算了斐波那契数列

1）黄金比例计算方法，使用 rint 函数对浮点数取整但不改变浮点数类型

1，1，2，3，5，8，13，21，34，55，89，……

#   斐波那契数,用黄金分割公式或通常所说的比奈公式，加上取整函数
n = np.arange(1, 9)
sqrt5 = np.sqrt(5)
phi = (1 + sqrt5)/2 #利用根号5计算黄金比例，或者直接用phi=1+0.618
print("比例：",phi)
print('\n')
fibonacci = np.rint((phi**n - (-1/phi)**n)/sqrt5)  #用rint()函数对浮点数取整但不改变浮点数类型
print("Fibonacci", fibonacci)

2）利用矩阵进行计算：用 matrix 函数创建矩阵

# 斐波那契数,用矩阵来表示斐波那契数列的递推关系
F = np.matrix([[1, 1], [1, 0]])
print ("8th Fibonacci:", (F ** 10)[0, 0])

运行结果：

比例： 1.618033988749895

Fibonacci [ 1.  1.  2.  3.  5.  8. 13. 21.]
8th Fibonacci: 89

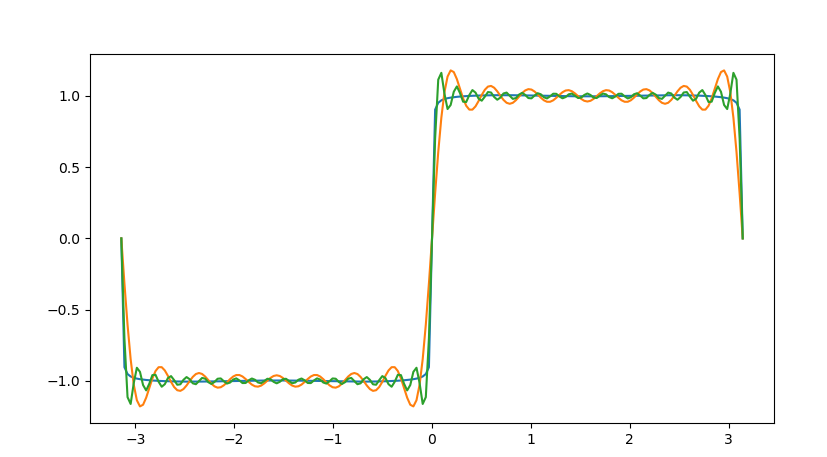
三、方波

方波可以近似表示为多个正弦波的叠加。任意一个方波信号都可以用无穷傅里叶级数来表示。

需要累加很多项级数，且级数越多结果越精确，这里取 k=99（可以分别设置为9，50，1000等进行测试观察生成效果） 以保证足够的精度。绘制方波的步骤如下。

1) 初始化 t 和 k 开始，并将函数值初始化为

m = np.linspace(-np.pi, np.pi, 201) #从 -pi 到 pi 上均匀分布的 201 个点
k = np.arange(1,99)   # k=99 以保证足够的精度，如图中的9 20 99显示的波形
k = 2 * k - 1
f = np.zeros_like(m)

2）使用 sin()求正弦函数，用sum()数计算各项级数：

for i in range(len(m)):  #使用 sin 和 sum 函数进行计算
    f[i] = np.sum(np.sin(k * m[i])/k)
f = (4 / np.pi) * f

3）绘制波形

plt.plot(t, f)
plt.show()

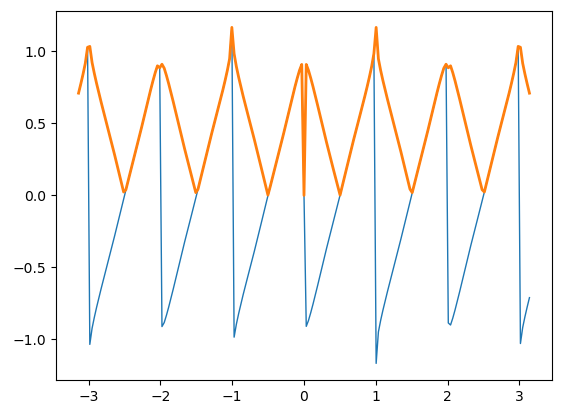
四、锯齿波和三角波

锯齿波和三角波也是常见的波形。和方波类似，也可以将它们表示成无穷傅里叶级数。对锯齿波取绝对值即可得到三角波。锯齿波的无穷级数表达式如下：

import numpy as np
import matplotlib.pyplot as plt

t = np.linspace(-np.pi, np.pi, 201)
k = np.arange(1, 99)
f = np.zeros_like(t)
for i in range(len(t)):
    f[i] = np.sum(np.sin(2 * np.pi * k * t[i])/k)

f = (-2 / np.pi) * f
plt.plot(t, f, lw=1.0)
plt.plot(t, np.abs(f), lw=2.0)
plt.show()

运行结果：