枚举子集的3种方式 -- C++描述

要求：

　　给定一个集合，枚举所有可能的子集。此处的集合是不包含重复元素的。

Method0: 增量构造法

　　思路：每次选取一个元素至集合中，为了避免枚举重复的集合，此处要采用定序技巧 -- 除了第一个元素，每次选取必须要比集合中的前一个元素要大！

　　

// A 为原集合；
// B 为子集，每次调用函数即会打印一次
// cur 为子集元素个数
void print_subset0(int *A, int *B, int N, int cur) {
    for(int i=0; i<cur; i++) {
        printf("%5d", B[i]);
    }
    printf("\n");
    if( cur < N ) {
        for( int i=0; i<N; i++ ) {
            if( !cur || A[i] > B[cur-1] ) {
                B[cur] = A[i];
                print_subset0(A, B, N, cur+1);
            }
        }
    }
}
 
int main() {
    int Length = 3;
    int A[Length] = {1, 3, 2};
    printf("Method0:\n");
    int B[Length] = {0};
    print_subset0(A, B, Length, 0);
    printf("\n");
    return 0;
}

　　采用的是递归调用，但此处不需要return语句，因为当没有元素可用于枚举时，就不会调用函数，也就是不会继续递归。

　　 此函数输出的子集中是包含空集的，如果不想用空集，则需判断 cur 是否为0，不为0才打印子集

　　 测试样例的输出结果（包含空集）：

　　　　

Method1: 位向量法

　　思路：1个容量为N的集合，每个位置0～N-1，对于每个子集，要么被选中，要么没被选中。枚举每一个位置的状态，可得到各种子集。

　　

// A 为原集合；
// A 为原集合
// used为当前A中每个位置的元素的状态（选中或未被选中）
// cur代表现在枚举A[cur]的状态
void print_subset1(int *A, int *used, int N, int cur) {
    if( cur == N ) {
        for(int i=0; i<N; i++) {
            if( used[i] ) {
                printf("%5d", A[i]);
            }
        }
        printf("\n");
        return ;
    }
    used[cur] = 0;
    print_subset1(A, used, N, cur+1);
    used[cur] = 1;
    print_subset1(A, used, N, cur+1);
}
 
int main() {
    int Length = 3;
    int A[Length] = {1, 3, 2};
 
    printf("Method1:\n");
    int B[Length] = {0};
    print_subset1(A, B, Length, 0);
    printf("\n");
 
    return 0;
}

　　同样是递归枚举，这里需要用return终止递归，终止条件就是cur == N即枚举了一种子集，然后输出　　

　　此函数的输出是包含空集的，如果不想要空集，则需要判断used函数是否全为0，如果全为0，则不输出

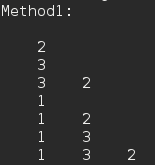
　　样例输出（包含空集）：

　　　　

Method10: 二进制法

　　类似于位向量法，同样也是枚举各个位置的状态，但这次用二进制表示，二进制长度为N，与原集合大小相同。二进制的第 i 位代表原集合中的第 i 位是否被选中，枚举各种情况。集合大小为N，就是2的N次种方式。

　　

void print_subset10(int *A, int N, int seq) {
    for(int i=0; i<N; i++) {
        if( seq & (1<<i) ) {
            printf("%5d", A[i]);
        }
    }
    printf("\n");
}
 
int main() {
    int Length = 3;
    int A[Length] = {1, 3, 2};
    printf("Method10:\n");
    for(int i=0; i<(1<<Length); i++) {
        print_subset10(A, Length, i);
    }
    printf("\n");
    return 0;
}

　　这种方式很好写，也很好记，但问题是，因为函数中的形参seq是int型的，所以N最大也就只能32，如果long long，那N也只能最大64，再超过64，就需要用大数或其它表示方式表示了。

　　 如果不想要空集，可以将main函数中的 i 从1枚举起。

　　样例输出结果（包含空集）：

　　　　

参考资料： 《算法竞赛入门经典（第2版）》