猪猪的机器学习笔记（十四）EM算法

EM算法

作者：樱花猪

 

摘要：

本文为七月算法（julyedu.com）12月机器学习第十次次课在线笔记。EM算法全称为Expectation Maximization Algorithm，既最大期望算法。它是一种迭代的算法，用于含有隐变量的概率参数模型的最大似然估计和极大后验概率估计。EM算法经常用于机器学习和机器视觉的聚类领域，是一个非常重要的算法。而EM算法本身从使用上来讲并不算难，但是如果需要真正的理解则需要许多知识的相互串联。

引言：

     EM算法是机器学习十大经典算法之一。EM算法既简单有复杂，简单的在于他的思想而复杂则在于他的数学推理和复杂的概率公式。作为我这个新手来讲，决定先捡大的部分，因此文章我们会更加着重概念的理解，至于公式的推导，在上过课以后其实也不是那么的困难，主要一点是你需要有非常扎实的数学功底，EM算法的推导过程基本上涵盖了我们前面所有讲到的数学知识。因此，如果看不懂EM算法大概是因为基础知识太弱了需要补习。

预备知识：

贝叶斯网络、概率论与数理统计、凸优化

一、EM算法

实际问题：随机挑选10000位志愿者，测量他们的身高：若样本中存在男性和女性，身高分别服从N(μ1,σ1)和N(μ2,σ2)的分布，试估计μ1,σ1,μ2,σ2。

1、提出

假定有训练集，包含m个独立样本，希望从中找到该组主句的模型的参数。

2、建立目标函数

我们利用极大似然估计来建立目标函数：

z是隐随机变量，不方便直接找到参数估计。

策略：计算下界，求该下界的最大值；重复该过程，直到收敛到局部最大值。

利用Jesenbu不等式，寻找尽量紧的下界

令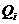是z的某一个分布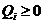，有：

LOG的曲线。

为了使等号成立：

有：

根据上述推导，有EM算法框架：

E-step（求条件分布）

M-step（求期望）

相互迭代，求的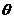

 

二、高斯混合模型GMM

目的：随机变量X是有K个高斯分布混合而成，取各个高斯分布的概率为π1π2...πK，第i个高斯分布的均值为μi，方差为Σi。若观测到随机变量X的一系列样本x1,x2,...,xn，试估计参数π，μ，Σ。

1、直观求解：

对数似然函数：

由于在对数函数里面又有加和，我们没法直接用求导解方程的办法直接求得极大值。为了解决这个问题，我们分成两步。

 

第一步：估计数据由每个组份生成的概率

对于每个样本xi，它由第k个组份生成的概率为：

上式中的μ和Σ也是待估计的值，因此采样迭代法：在计算γ(i,k)时假定μ和Σ已知；γ(i,k)亦可看成组份k在生成数据xi时所做的贡献。

第二步：估计每个组份的参数

对于所有的样本点，对于组份k而言，可看做生成了这些点。组份k是一个标准的高斯分布，利用上面的结论：

2、EM方法求解：

E-step:

M-step：将多项分布和高斯分布的参数带入

对均值求偏导：

令上式等于0，解的均值：

 

高斯分布的方差：求偏导，等于0

 

多项分布的参数：

考察M-step的目标函数，对于φ，删除常数项：

有：

由于多项分布的概率和为1，建立拉格朗日方程：

求偏导，等于0：

更加感观的讲解，参见：

http://blog.csdn.net/zouxy09/article/details/8537620

来自为知笔记(Wiz)