codeforces 342D Xenia and Dominoes（状压dp+容斥）

转载请注明出处： http://www.cnblogs.com/fraud/          ——by fraud

D. Xenia and Dominoes

Xenia likes puzzles very much. She is especially fond of the puzzles that consist of domino pieces. Look at the picture that shows one of such puzzles.

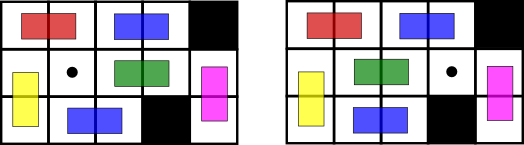
A puzzle is a 3 × n table with forbidden cells (black squares) containing dominoes (colored rectangles on the picture). A puzzle is calledcorrect if it meets the following conditions:

• each domino occupies exactly two non-forbidden cells of the table;
• no two dominoes occupy the same table cell;
• exactly one non-forbidden cell of the table is unoccupied by any domino (it is marked by a circle in the picture).

To solve the puzzle, you need multiple steps to transport an empty cell from the starting position to some specified position. A move is transporting a domino to the empty cell, provided that the puzzle stays correct. The horizontal dominoes can be moved only horizontally, and vertical dominoes can be moved only vertically. You can't rotate dominoes. The picture shows a probable move.

Xenia has a 3 × n table with forbidden cells and a cell marked with a circle. Also, Xenia has very many identical dominoes. Now Xenia is wondering, how many distinct correct puzzles she can make if she puts dominoes on the existing table. Also, Xenia wants the circle-marked cell to be empty in the resulting puzzle. The puzzle must contain at least one move.

Help Xenia, count the described number of puzzles. As the described number can be rather large, print the remainder after dividing it by1000000007 (109 + 7).

Input

The first line contains integer n (3 ≤ n ≤ 104) — the puzzle's size. Each of the following three lines contains n characters — the description of the table. The j-th character of the i-th line equals "X" if the corresponding cell is forbidden; it equals ".", if the corresponding cell is non-forbidden and "O", if the corresponding cell is marked with a circle.

It is guaranteed that exactly one cell in the table is marked with a circle. It is guaranteed that all cells of a given table having at least one common point with the marked cell is non-forbidden.

Output

Print a single number — the answer to the problem modulo 1000000007 (109 + 7).

Sample test(s)

input

5
....X
.O...
...X.

output

1

input

5
.....
.O...
.....

output

2

input

3
...
...
..O

output

4

Note

Two puzzles are considered distinct if there is a pair of cells that contain one domino in one puzzle and do not contain it in the other one.

好题。

问有几种排法使得有至少一块多米诺骨牌可以移动。其中O点和X点不能放置多米诺骨牌，但要求最终的可以通过O点移动。X点表示障碍。

要求的即为四个方向中至少有一个方向可以移动，所以，容斥的时候，把那个用X表示好，然后类似poj的铺砖问题，状压。

 //#####################
 //Author:fraud
 //Blog: http://www.cnblogs.com/fraud/
 //#####################
 #include <iostream>
 #include <sstream>
 #include <ios>
 #include <iomanip>
 #include <functional>
 #include <algorithm>
 #include <vector>
 #include <string>
 #include <list>
 #include <queue>
 #include <deque>
 #include <stack>
 #include <set>
 #include <map>
 #include <cstdio>
 #include <cstdlib>
 #include <cmath>
 #include <cstring>
 #include <climits>
 #include <cctype>
 using namespace std;
 #define XINF INT_MAX
 #define INF 0x3FFFFFFF
 #define MP(X,Y) make_pair(X,Y)
 #define PB(X) push_back(X)
 #define REP(X,N) for(int X=0;X<N;X++)
 #define REP2(X,L,R) for(int X=L;X<=R;X++)
 #define DEP(X,R,L) for(int X=R;X>=L;X--)
 #define CLR(A,X) memset(A,X,sizeof(A))
 #define IT iterator
 typedef long long ll;
 typedef pair<int,int> PII;
 typedef vector<PII> VII;
 typedef vector<int> VI;
 #define MAXN 100010
 char a[][MAXN];
 int dp[MAXN][];
 int m[MAXN];
 const int MOD=;
 int n;
 int gao(){
     CLR(m,);
     for(int i=;i<;i++){
         for(int j=;j<n;j++){
             if(a[i][j]=='X')m[j]|=<<i;
         }
     }
     CLR(dp,);
     dp[][]=;
     for(int i=;i<n;i++){
         for(int j=;j<;j++){
             for(int k=;k<;k++){
                 if(k&m[i])continue;
                 int x=j|m[i]|k;
                 if((j&(k|m[i]))==&&(x==||x==||x==)){
                     dp[i+][k]+=dp[i][j];
                     if(dp[i+][k]>=MOD)dp[i+][k]-=MOD;
                 }
             }
         }
     }
     return dp[n][];
 }
 bool check(int x,int y){
     if(x>=&&x<&&y>=&&y<n&&a[x][y]=='.')return ;
     return ;
 }
 int dx[]={-,,,};
 int dy[]={,,-,};
 int main()
 {
     ios::sync_with_stdio(false);
     int ci,cj;
     int x[],y[],tot=;
     cin>>n;
     for(int i=;i<;i++){
         for(int j=;j<n;j++){
             cin>>a[i][j];
             if(a[i][j]=='O')ci=i,cj=j,a[i][j]='X';
         }
     }
     int ans=;
     for(int i=;i<;i++){
         int t=i;
         tot=;
         int c=;
         for(int j=;j<;j++){
             if(t&){
                 x[tot]=dx[j];
                 y[tot++]=dy[j];
                 x[tot]=dx[j]*;
                 y[tot++]=dy[j]*;
                 c++;
             }
             t>>=;
         }
         bool flag=;
         for(int j=;j<tot;j++){
             if(check(ci+x[j],cj+y[j]))flag=;
         }
         if(flag){
             for(int j=;j<tot;j++){
                 a[ci+x[j]][cj+y[j]]='X';
             }
             if(c&)ans+=gao();
             else ans-=gao();
             if(ans>=MOD)ans-=MOD;
             else if(ans<)ans+=MOD;
             for(int j=;j<tot;j++){
                 a[ci+x[j]][cj+y[j]]='.';
             }
         }
     }
     cout<<ans<<endl;

     return ;
 }

代码君