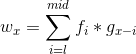洛谷4721 【模板】分治 FFT
传送门
久违的多项式全家桶= =+
分治NTT 用的就是cdq分治的思想 对于当前递归到的区间[l,r] 我们处理出[l,mid]对[mid+1,r]答案的贡献
然后分治递归求解就可以啦qwq
这个贡献是前一半卷积的答案加过去就可以啦
对于x的贡献
附代码。
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cmath>
#define ll long long
#define mdn 998244353
#define G 3
#define mxn 200010
using namespace std;
int ksm(int bs,int mi)
{
int ans=1;
while(mi)
{
if(mi&1) ans=(ll)ans*bs%mdn;
bs=(ll)bs*bs%mdn; mi>>=1;
}
return ans;
}
int rev[mxn],inv;
int init(int n)
{
int lim=1,l=0;
while(lim<n) lim<<=1,l++;
for(int i=1;i<lim;i++)
rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
inv=ksm(lim,mdn-2);
return lim;
}
void NTT(int *a,int n,int f)
{
for(int i=0;i<n;i++) if(rev[i]>i) swap(a[rev[i]],a[i]);
for(int k=2;k<=n;k<<=1)
{
int Wn=ksm(G,(mdn-1)/k),mid=k>>1;
if(f) Wn=ksm(Wn,mdn-2);
for(int w=1,i=0;i<n;i+=k,w=1)
for(int j=0;j<mid;j++,w=(ll)w*Wn%mdn)
{
int x=a[i+j],y=(ll)w*a[i+mid+j]%mdn;
a[i+j]=(x+y)%mdn;
a[i+mid+j]=(x-y+mdn)%mdn;
}
}
if(f) for(int i=0;i<n;i++) a[i]=(ll)a[i]*inv%mdn;
}
int f[mxn],g[mxn],h[mxn],a[mxn],b[mxn];
void cdq(int l,int r)
{
if(l==r) return;
int mid=(l+r)>>1;
cdq(l,mid); int lim = init(r-l+1);
for(int i=0;i<=mid-l;i++) a[i]=f[l+i];
for(int i=mid-l+1;i<=lim;i++) a[i]=0;
for(int i=0;i<=r-l;i++) b[i]=g[i];
for(int i=r-l+1;i<=lim;i++) b[i]=0;
NTT(a,lim,0); NTT(b,lim,0);
for(int i=0;i<lim;i++) a[i]=(ll)a[i]*b[i]%mdn;
NTT(a,lim,1);
//for(int i=0;i<lim;i++) printf("%d ",a[i]);
for(int i=mid+1;i<=r;i++) f[i]=(ll)(f[i]+a[i-l])%mdn;
cdq(mid+1,r);
}
int n;
int main()
{
scanf("%d",&n);
for(int i=1;i<n;i++) scanf("%d",&g[i]);
f[0]=1;
cdq(0,n);
for(int i=0;i<n;i++) printf("%d ",f[i]);
return 0;
}洛谷4721 【模板】分治 FFT的更多相关文章
- 洛谷.4721.[模板]分治FFT(NTT)
题目链接 换一下形式:\[f_i=\sum_{j=0}^{i-1}f_jg_{i-j}\] 然后就是分治FFT模板了\[f_{i,i\in[mid+1,r]}=\sum_{j=l}^{mid}f_jg ...
- 解题:洛谷4721 [模板]分治FFT
题面 这是CDQ入门题,不要被题目名骗了,这核心根本不在不在FFT上啊=.= 因为后面的项的计算依赖于前面的项,不能直接FFT.所以用CDQ的思想,算出前面然后考虑给后面的贡献 #include< ...
- 洛谷 P4721 [模板]分治FFT —— 分治FFT / 多项式求逆
题目:https://www.luogu.org/problemnew/show/P4721 分治做法,考虑左边对右边的贡献即可: 注意最大用到的 a 的项也不过是 a[r-l] ,所以 NTT 可以 ...
- 【洛谷4721】【模板】分治FFT(CDQ分治_NTT)
题目: 洛谷 4721 分析: 我觉得这个 "分治 FFT " 不能算一种特殊的 FFT ,只是 CDQ 分治里套了个用 FFT (或 NTT)计算的过程,二者是并列关系而不是偏正 ...
- 洛谷P3373 [模板]线段树 2(区间增减.乘 区间求和)
To 洛谷.3373 [模板]线段树2 题目描述 如题,已知一个数列,你需要进行下面两种操作: 1.将某区间每一个数加上x 2.将某区间每一个数乘上x 3.求出某区间每一个数的和 输入输出格式 输入格 ...
- 洛谷 4721 【模板】分治 FFT——分治FFT / 多项式求逆
题目:https://www.luogu.org/problemnew/show/P4721 分治FFT:https://www.cnblogs.com/bztMinamoto/p/9749557.h ...
- POJ 1741.Tree and 洛谷 P4178 Tree-树分治(点分治,容斥版) +二分 模板题-区间点对最短距离<=K的点对数量
POJ 1741. Tree Time Limit: 1000MS Memory Limit: 30000K Total Submissions: 34141 Accepted: 11420 ...
- 洛谷.1919.[模板]A*B Problem升级版(FFT)
题目链接:洛谷.BZOJ2179 //将乘数拆成 a0*10^n + a1*10^(n-1) + ... + a_n-1的形式 //可以发现多项式乘法就模拟了竖式乘法 所以用FFT即可 注意处理进位 ...
- 洛谷.3803.[模板]多项式乘法(FFT)
题目链接:洛谷.LOJ. FFT相关:快速傅里叶变换(FFT)详解.FFT总结.从多项式乘法到快速傅里叶变换. 5.4 又看了一遍,这个也不错. 2019.3.7 叕看了一遍,推荐这个. #inclu ...
- [洛谷P3806] [模板] 点分治1
洛谷 P3806 传送门 这个点分治都不用减掉子树里的了,直接搞就行了. 注意第63行 if(qu[k]>=buf[j]) 不能不写,也不能写成>. 因为这个WA了半天...... 如果m ...
随机推荐
- 【转】django 正则URL 匹配
django 正则URL 匹配 转自:https://www.cnblogs.com/chenkeven/articles/9305260.html 一.引子 在day17 作业中,我们查看主机详细 ...
- Alisha’s Party
Alisha’s Party Time Limit: 3000/2000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others) ...
- Jenkins搭建(by tomcat)
Jenkins官网https://jenkins.io/download/下载最新版本jenkins.war 把jenkins.war放到tomcat-jenkins的webapps下 修改tomca ...
- 微信小程序的开发框架
wxss:是一套样式语言,用来描述wxml的组件样式:小程序在css基础上做的修改和扩充的版本 css:是一套样式语言,样式表,用来描述xml和html文件样式的呈现: 设备像素:是图片在设备上显示的 ...
- [LeetCode] 136. Single Number(位操作)
传送门 Description Given an array of integers, every element appears twice except for one. Find that si ...
- JQ获取当前根目录
function getRootPath_web() { //获取当前网址,如: http://localhost:8083/uimcardprj/share/meun.jsp ...
- oracle创建sequence序列语法
在oracle中sequence就是序号,每次取的时候它会自动增加.sequence与表没有关系 1.create sequence create sequence SEQ_LOG_ID minval ...
- C++学习笔记(三)--数组、字符串
1.数组,C++中不允许数组的下标值为变量,只能是常量或者常量表达式,必须先定义后使用.数组赋初值几种常见方式: int a[] = {1,2,3,4,5}: int a[4] = {2,1,3,4} ...
- 查找idt table 所對應的page table in Linux
#include <linux/kernel.h> #include <linux/module.h> #include <linux/types.h> #incl ...
- 2019牛客暑期多校训练营(第一场) - E - ABBA - 贪心 - dp - 组合
https://ac.nowcoder.com/acm/contest/881/E 从dp的角度来看是比较正常的.无后效性来源于前面只要的合法的方案分配,那么对后面造成的影响就只有A,B的数目. 从贪 ...