POJ 1269 Intersecting Lines (判断直线位置关系)

题目链接：POJ 1269

Problem Description

We all know that a pair of distinct points on a plane defines a line and that a pair of lines on a plane will intersect in one of three ways: 1) no intersection because they are parallel, 2) intersect in a line because they are on top of one another (i.e. they are the same line), 3) intersect in a point. In this problem you will use your algebraic knowledge to create a program that determines how and where two lines intersect.

Your program will repeatedly read in four points that define two lines in the x-y plane and determine how and where the lines intersect. All numbers required by this problem will be reasonable, say between -1000 and 1000.

Input

The first line contains an integer N between 1 and 10 describing how many pairs of lines are represented. The next N lines will each contain eight integers. These integers represent the coordinates of four points on the plane in the order x1y1x2y2x3y3x4y4. Thus each of these input lines represents two lines on the plane: the line through (x1,y1) and (x2,y2) and the line through (x3,y3) and (x4,y4). The point (x1,y1) is always distinct from (x2,y2). Likewise with (x3,y3) and (x4,y4).

Output

There should be N+2 lines of output. The first line of output should read INTERSECTING LINES OUTPUT. There will then be one line of output for each pair of planar lines represented by a line of input, describing how the lines intersect: none, line, or point. If the intersection is a point then your program should output the x and y coordinates of the point, correct to two decimal places. The final line of output should read "END OF OUTPUT".

Sample Input

5
0 0 4 4 0 4 4 0
5 0 7 6 1 0 2 3
5 0 7 6 3 -6 4 -3
2 0 2 27 1 5 18 5
0 3 4 0 1 2 2 5

Sample Output

INTERSECTING LINES OUTPUT
POINT 2.00 2.00
NONE
LINE
POINT 2.00 5.00
POINT 1.07 2.20
END OF OUTPUT

Solution

题意

\(n\) 组样例。每组样例给定两条直线，判断直线是平行，重合还是相交。若相交求交点。

题解

叉积

• 判断共线：

若 \(\boldsymbol{ab}\) 与 \(\boldsymbol{cd}\) 共线，则 \(\boldsymbol{ab} \times \boldsymbol{cd} = 0\)。

• 判断重合：

若 \(\boldsymbol{ab}\) 与 \(\boldsymbol{cd}\) 重合，则 \(\boldsymbol{bc} \times \boldsymbol{ad} = 0\)。

• 判断平行：

共线且不重合。

• 求交点：

首先要满足相交。

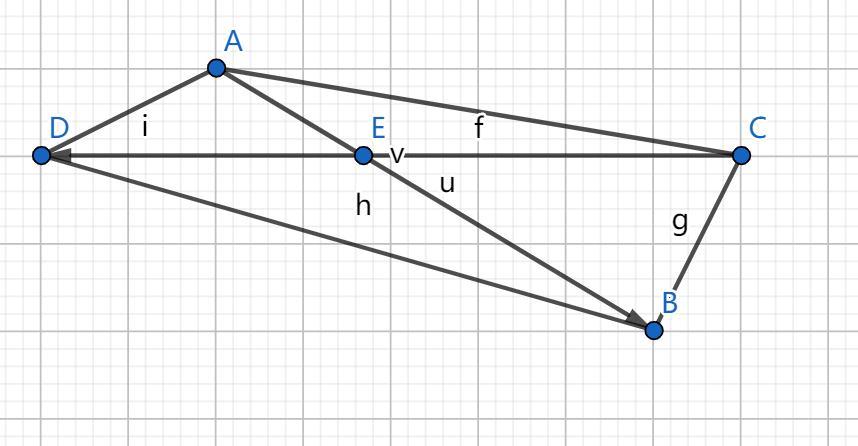
如上图，求 \(\boldsymbol{AB}\) 与 \(\boldsymbol{CD}\) 的交点 \(E\)。

\[\frac{AE}{BE} = \frac{S_{\triangle ACD}}{S_{\triangle BCD}} = \frac{|\boldsymbol{CA} \times \boldsymbol{CD}|}{|\boldsymbol{CB} \times \boldsymbol{CD}|}
\]

\[\boldsymbol{AE} = \frac{|\boldsymbol{AE}|}{|\boldsymbol{AB}|} \boldsymbol{AB} = \frac{|\boldsymbol{AE}|}{|\boldsymbol{AE}| + |\boldsymbol{EB}|} \boldsymbol{AB} = \frac{S_{\triangle ACD}}{S_{\triangle ACD} + S_{\triangle BCD}} \boldsymbol{AB}
\]

设原点为 \(O\)，则

\[\boldsymbol{OE} = \boldsymbol{OA} + \boldsymbol{AE}
\]

\(\boldsymbol{OE}\) 即为点 \(E\) 的坐标。

Code

#include <cstdio>
#include <iostream>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll;
typedef double db;
const db eps = 1e-10;
const db pi = acos(-1.0);
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll maxn = 1e5 + 10;
inline int dcmp(db x) {
    if(fabs(x) < eps) return 0;
    return x > 0? 1: -1;
}
class Point {
public:
    double x, y;
    Point(double x = 0, double y = 0) : x(x), y(y) {}
    void input() {
        scanf("%lf%lf", &x, &y);
    }
    bool operator<(const Point &a) const {
        return (!dcmp(x - a.x))? dcmp(y - a.y) < 0: x < a.x;
    }
    bool operator==(const Point &a) const {
        return dcmp(x - a.x) == 0 && dcmp(y - a.y) == 0;
    }
    db dis2(const Point a) {
        return pow(x - a.x, 2) + pow(y - a.y, 2);
    }
    db dis(const Point a) {
        return sqrt(dis2(a));
    }
    db dis2() {
        return x * x + y * y;
    }
    db dis() {
        return sqrt(dis2());
    }
    Point operator+(const Point a) {
        return Point(x + a.x, y + a.y);
    }
    Point operator-(const Point a) {
        return Point(x - a.x, y - a.y);
    }
    Point operator*(double p) {
        return Point(x * p, y * p);
    }
    Point operator/(double p) {
        return Point(x / p, y / p);
    }
    db dot(const Point a) {
        return x * a.x + y * a.y;
    }
    db cross(const Point a) {
        return x * a.y - y * a.x;
    }
};
typedef Point Vector;
class Line {
public:
    Point s, e;
    Line() {}
    Line(Point s, Point e) : s(s), e(e) {}
    void input() {
        scanf("%lf%lf%lf%lf", &s.x, &s.y, &e.x, &e.y);
    }
    int toLeftTest(Point p) {
        if((e - s).cross(p - s) > 0) return 1;
        else if((e - s).cross(p - s) < 0) return -1;
        return 0;
    }
    // 共线
    bool collinear(Line l) {
        if(dcmp((e - s).cross(l.e - l.s)) == 0) {
            return 1;
        }
        return 0;
    }
    // 同线
    bool same(Line l) {
        if(dcmp((l.s - e).cross(l.e - s)) == 0) {
            return 1;
        }
        return 0;
    }
    // 平行
    bool parallel(Line l) {
        return collinear(l) && (!same(l));
    }
    // 直线与直线交点
    Point crosspoint(Line l) {
		double a1 = (l.e - l.s).cross(s - l.s);
		double a2 = (l.e - l.s).cross(e - l.s);
        Point ans = s + (e - s) * (-a1) / (a2 - a1);
        if(dcmp(ans.x) == 0) ans.x = 0;
        if(dcmp(ans.y) == 0) ans.y = 0;
		return ans;
	}
    // 直线与直线位置关系 0-重合 1-平行 2-相交
    int linecrossline (Line l) {
        if(dcmp((e - s).cross(l.e - l.s)) == 0) {
            if(dcmp((l.s - e).cross(l.e - s)) == 0) {
                return 0;
            }
            return 1;
        }
        return 2;
    }
};
Line l1, l2;
int main() {
    int T;
    scanf("%d", &T);
    printf("INTERSECTING LINES OUTPUT\n");
    while(T--) {
        l1.input();
        l2.input();
        if(l1.linecrossline(l2) == 0) {
            printf("LINE\n");
        } else if(l1.linecrossline(l2) == 1) {
            printf("NONE\n");
        } else {
            Point ans = l1.crosspoint(l2);
            printf("POINT %.2lf %.2lf\n", ans.x, ans.y);
        }
    }
    printf("END OF OUTPUT\n");
    return 0;
}