ZOJ 3822 ( 2014牡丹江区域赛D题) (概率dp)

http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=5376

题意：每天往n*m的棋盘上放一颗棋子，求多少天能将棋盘的每行每列都至少有一颗棋子的期望

分析： 我们来分析一波； 讲解一下弱弱的我的解题思路

（1）首先可以想到的是设一个 dp[val]  表示 当前用了val 个旗子距离目标状态还有几天的概率。但是我们可以发现单纯的一个状态val 是不能表示出准确的状态 ， 比如说现在只是知道了我使用了多少的旗子，当前不知道有多少行和列是有旗子的；

（2）所以我们改变dp为 dp[val][i][j]  表示 用了val个旗子，有i行和j列有旗子了，到目标状态还有几天的概率。注意我们设的是概率dp[val][i][j] 有一个状态是val天数了 ， 所以3我们可以先把概率求出来，最后在计算期望

(3)状态转移：有四种状态

(1)加入一个是放在记录的行中与列中：dp[val+1][i][j] -> dp[val][i][j] *p1;

(2)加入一个是放在没有记录过的行中与记录过的列中： dp[val+1][i+1][j] -> dp[val][i][j]*p2;

(3)加入一个是放在记录过的行中与没有记录过的列中：dp[val+1][i][j+1]->dp[val][i][j]*p3;

(4)加入一个是放在没有记录的行中与没有记录过的列中：dp[val+1][i+1][j+1]->dp[val][i][j]*p4;

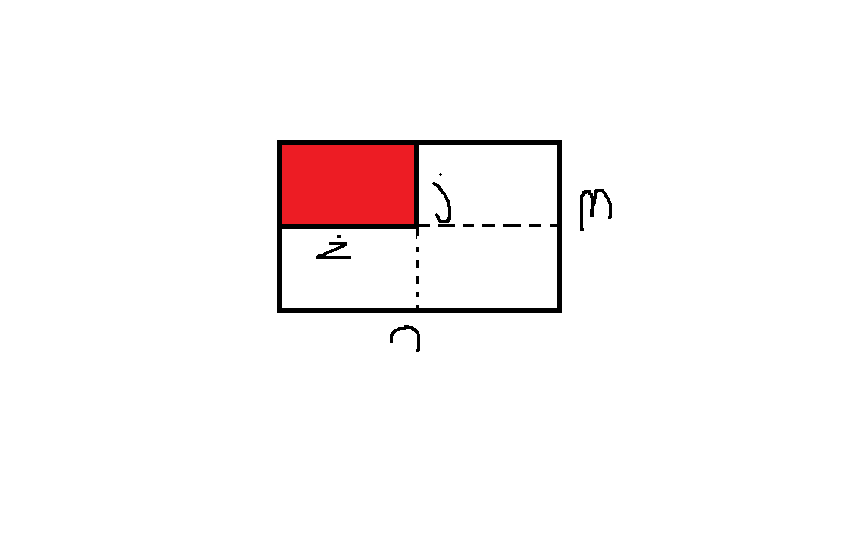
p1,p2,p3,p4求法可以观察下图：

图中红色部分可视为j行k列已经至少有一个棋子了

#include<bits/stdc++.h>
using namespace std;
double dp[][][];
int main() {
    int t;
    cin >> t;
    int k=;
    while(t--) {
      int n,m;scanf("%d%d",&n,&m);
      memset(dp,,sizeof(dp));
      dp[][][]=;
      for(int val= ; val<n*m ; val++) ///放其
      {
          for(int i= ; i<=n ; i++)
            {
                for(int j= ; j<=m ; j++)
                {
                    if(dp[val][i][j]==) continue;
                    double p1,p2,p3,p4;
                    if( i<n  ||j<m){
                    p1=(i*j-val)*1.0/(n*m-val);
                    dp[val+][i][j]+=dp[val][i][j]*p1;
                    }
                    p2=j*(n-i)*1.0/(n*m-val);
                    dp[val+][i+][j]+=dp[val][i][j]*p2;
                    p3=i*(m-j)*1.0/(n*m-val);
                    dp[val+][i][j+]+=dp[val][i][j]*p3;
                    p4=(n-i)*(m-j)*1.0/(n*m-val);
                    dp[val+][i+][j+]+=dp[val][i][j]*p4;
 
                }
            }
      }
      double ans=;
      for(int val= ; val<=n*m ; val++)
      {
          ans+=dp[val][n][m]*val;
          //cout<<dp[val][n][m]<<endl;
      }
      printf("%.12f\n",ans);
 
    }
    return ;
}