1443：【例题4】Addition Chains

1443：【例题4】Addition Chains

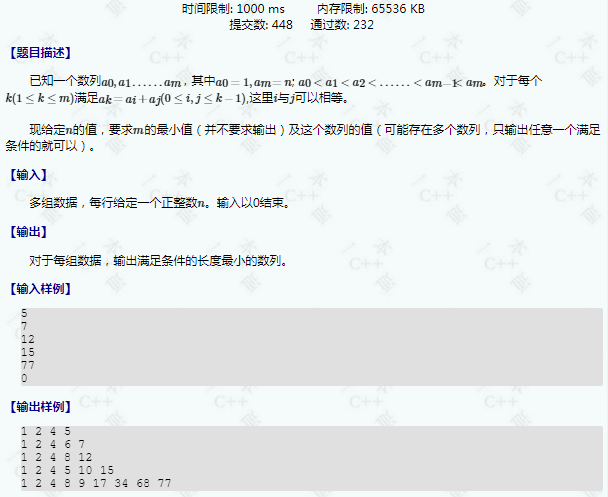
题解

注释在代码里

注意优化搜索顺序以及最优化剪枝

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<string>
#include<queue>
#include<functional>

using namespace std;

int n,minn,ans[],a[];
//n是序列的最大值
//minn是拆数字最小层数
//ans存答案
//a是一个过程中起记录作用的数组 

void dfs(int x)  //递归第x层
{
    if(x->minn) return ;  //超过最小层数，剪枝
    if(a[x-]>n) return;   //上一层的数字大于最大值n，剪枝
    if(a[x-]==n)  //上一层的数字=n，有希望构成一个完整解答
    {
        if((x-1)>=minn) return; //很遗憾，层数超了
        minn=x-;   //记下暂定答案
        for(int i=;i<x;i++) ans[i]=a[i];
    }
    else
    {
        for(int j=x-;j>=;j--)
        //题目要求ak=ai+aj,倒着枚举一下，看看能否继续扩展下一层
        {
            if(a[x-]+a[j]<=n)
            {
                a[x]=a[x-]+a[j];  //可以继续扩展
                dfs(x+);
                a[x]=;  //回溯
            }
        }
    }
}

int main()
{
    while(scanf("%d",&n)!=EOF) //输入非空
    {
        if(n==) break;
        else
        {
            a[]=;  //初始化第一层为1
            minn=;  //拆数字的最小层数
            dfs();  //从第二层开始递归
            for(int i=;i<=minn;i++) printf("%d ",ans[i]); //确定层数，输出答案
            printf("\n");
        }
    }
    return ;
}

---

特别鸣谢

orz  神仙