仙人掌图判定及求直径HDU3594 BZOJ1023

https://wenku.baidu.com/view/ce296043192e45361066f575.html   //仙人掌图基础知识3个判定条件

http://blog.csdn.net/yihuikang/article/details/7904347  //参考代码

题目：HDU 3594

Cactus

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2042    Accepted Submission(s): 950

Problem Description

1. It is a Strongly Connected graph.
2. Each edge of the graph belongs to a circle and only belongs to one circle.
We call this graph as CACTUS.

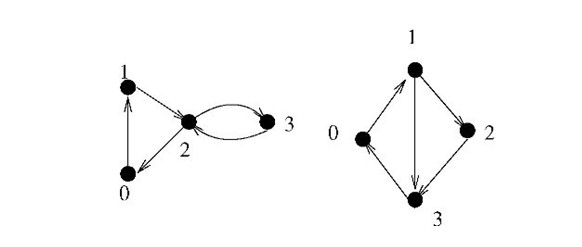
There is an example as the figure above. The left one is a cactus, but the right one isn’t. Because the edge (0, 1) in the right graph belongs to two circles as (0, 1, 3) and (0, 1, 2, 3).

 

Input

The input consists of several test cases. The first line contains an integer T (1<=T<=10), representing the number of test cases.
For each case, the first line contains a integer n (1<=n<=20000), representing the number of points.
The following lines, each line has two numbers a and b, representing a single-way edge (a->b). Each case ends with (0 0).
Notice: The total number of edges does not exceed 50000.

 

Output

For each case, output a line contains “YES” or “NO”, representing whether this graph is a cactus or not.

 

Sample Input

2
4
0 1
1 2
2 0
2 3
3 2
0 0
4
0 1
1 2
2 3
3 0
1 3
0 0

 

Sample Output

YES
NO

 

#include<cstdio>
#include<cstring>
#include<iostream>
const int maxn=;
const int maxm=;
int index,n,tot,head[maxn],cnt[maxn],vis[maxn],dfn[maxn],low[maxn];
//dfn表示的是其在树中的深度，low表示其经过移动可达到的最大高度（最小深度）
bool flag;
struct Edge{
   int v,next;
}e[maxm];
void add(int u,int v) {
   e[tot].v=v;e[tot].next=head[u];head[u]=tot++;
}
void dfs(int u){
   int v;
   if(!flag) return;
   dfn[u]=low[u]=++index;
   vis[u]=;
   for(int i=head[u];i+;i=e[i].next){
    v=e[i].v;
    if(vis[v]==) {flag=false;return;}  //出现了横向边,性质1
    if(!vis[v]) {
        dfs(v);
        if(low[v]>dfn[u]) {flag=false;return;} //性质2，如果其子节点所能达到的最大高度小于父节点，那么子节点一定不能达到父节点，所以不是连通图
        if(low[v]<dfn[u]) {
            ++cnt[u];//经过u的环+1
            if(low[v]<low[u]) low[u]=low[v];//更新所能达到的最大高度。
        }
    }
    else if(low[v]<dfn[u]) {
        ++cnt[u];//经过u的环+1
        if(low[v]<low[u]) low[u]=low[v];//更新所能达到的最大高度。
    }
    if(cnt[u]>) {flag=false;return;} //性质3
   }
   vis[u]=;//以u为根节点 的子树访问完毕，如果再有访问的话就是横向边。
}
int main(){
   int _,u,v;
   for(scanf("%d",&_);_--;){
    scanf("%d",&n);
    tot=;
    for(int i=;i<=n;++i) {
        head[i]=-;
        vis[i]=cnt[i]=;
    }
    while(scanf("%d%d",&u,&v),u||v) add(u+,v+);
    flag=;
    index=;
    dfs();
    if(!flag|index<n) puts("NO");
    else puts("YES");
   }
}

 

 

BZOJ 1023

1023: [SHOI2008]cactus仙人掌图

Time Limit: 1 Sec  Memory Limit: 162 MB
Submit: 2670  Solved: 1109
[Submit][Status][Discuss]

Description

　　如果某个无向连通图的任意一条边至多只出现在一条简单回路（simple cycle）里，我们就称这张图为仙人掌
图（cactus）。所谓简单回路就是指在图上不重复经过任何一个顶点的回路。

　　举例来说，上面的第一个例子是一张仙人图，而第二个不是——注意到它有三条简单回路：（4，3，2，1，6
，5，4）、（7，8，9，10，2，3，7）以及（4，3，7，8，9，10，2，1，6，5，4），而（2，3）同时出现在前两
个的简单回路里。另外，第三张图也不是仙人图，因为它并不是连通图。显然，仙人图上的每条边，或者是这张仙
人图的桥（bridge），或者在且仅在一个简单回路里，两者必居其一。定义在图上两点之间的距离为这两点之间最
短路径的距离。定义一个图的直径为这张图相距最远的两个点的距离。现在我们假定仙人图的每条边的权值都是1
，你的任务是求出给定的仙人图的直径。

Input

　　输入的第一行包括两个整数n和m（1≤n≤50000以及0≤m≤10000）。其中n代表顶点个数，我们约定图中的顶
点将从1到n编号。接下来一共有m行。代表m条路径。每行的开始有一个整数k（2≤k≤1000），代表在这条路径上
的顶点个数。接下来是k个1到n之间的整数，分别对应了一个顶点，相邻的顶点表示存在一条连接这两个顶点的边
。一条路径上可能通过一个顶点好几次，比如对于第一个样例，第一条路径从3经过8，又从8返回到了3，但是我们
保证所有的边都会出现在某条路径上，而且不会重复出现在两条路径上，或者在一条路径上出现两次。

Output

　　只需输出一个数，这个数表示仙人图的直径长度。

Sample Input

15 3
9 1 2 3 4 5 6 7 8 3
7 2 9 10 11 12 13 10
5 2 14 9 15 10 8
10 1
10 1 2 3 4 5 6 7 8 9 10

Sample Output

8
9

HINT

对第一个样例的说明：如图，6号点和12号点的最短路径长度为8，所以这张图的直径为8。

【注意】使用Pascal语言的选手请注意：你的程序在处理大数据的时候可能会出现栈溢出。

如果需要调整栈空间的大小，可以在程序的开头填加一句：{$M 5000000}，其中5000000即

指代栈空间的大小，请根据自己的程序选择适当的数值。

 

http://hzwer.com/4645.html  //参考代码

 

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int inf=0x3f3f3f3f;
const int maxn=;
int n,m,cnt,ind,ans;
int last[maxn],deep[maxn],f[maxn];//f是其到子节点中最大路径长度
int low[maxn],dfn[maxn],fa[maxn];
int a[maxn<<],q[maxn<<],l,r;
struct edge{int to,next;}e[maxn<<];
void insert(int u,int v){
   e[++cnt].to=v;e[cnt].next=last[u];last[u]=cnt;
   e[++cnt].to=u;e[cnt].next=last[v];last[v]=cnt;
}
void dp(int root,int x){
   int tot=deep[x]-deep[root]+;
   for(int i=x;i!=root;i=fa[i]) a[tot--]=f[i];
   a[tot]=f[root];
   tot=deep[x]-deep[root]+;
   for(int i=;i<=tot;++i) a[i+tot]=a[i];//二倍的原因是单调队列简化需要（这个操作我不太会)
   //感觉很有道理的样子
   q[]=;l=r=;
   for(int i=;i<=*tot;++i){  //单调队列
      while(l<=r&&i-q[l]>tot/) ++l;//题干要求最短路，大于tot/2的要删掉
      ans=max(ans,a[i]+i+a[q[l]]-q[l]) ;//i-q[l]是在主路径上i到q[l]的最短距离，再加上各自的子树中的f
      while(l<=r&&a[q[r]]-q[r]<=a[i]-i) --r;  //观察通项就可以的出这个了
      q[++r]=i;
   }
   for(int i=;i<=tot;++i)
    f[root]=max(f[root],a[i]+min(i-,tot-i+)); //有环的子节点要特殊更新一下
}
void dfs(int x)
{
 low[x]=dfn[x]=++ind;
 for(int i=last[x];i;i=e[i].next)
  if(e[i].to!=fa[x])
  {
   if(!dfn[e[i].to])
   {
    fa[e[i].to]=x;
    deep[e[i].to]=deep[x]+;
    dfs(e[i].to);
    low[x]=min(low[x],low[e[i].to]);
   }
   else low[x]=min(low[x],dfn[e[i].to]);
   if(dfn[x]<low[e[i].to])
   {
    ans=max(ans,f[x]+f[e[i].to]+);
    f[x]=max(f[x],f[e[i].to]+);
   }
  }
 for(int i=last[x];i;i=e[i].next)//处理成环的子树
  if(fa[e[i].to]!=x&&dfn[x]<dfn[e[i].to])
   dp(x,e[i].to);
}
int main()
{
 scanf("%d%d",&n,&m);
 for(int i=;i<=m;i++)
 {
  int k,a,b;
  scanf("%d%d",&k,&a);
  for(int i=;i<=k;i++)
  {
      scanf("%d",&b);
   insert(a,b);a=b;
  }
 }
 dfs();
 printf("%d\n",ans);
 return ;
}