MATLAB矩阵的表示

矩阵是matlab中最基本的数据对象。

l  矩阵的建立

l  冒号表达式

l  结构矩阵和单元矩阵

1.矩阵的建立

（1）利用直接输入法建立矩阵:将矩阵的元素用中括号括起来，按矩阵行的顺序输入各元素，同一行的各元素之间用逗号或空格分隔，不同行的元素之间用分号分隔。

>> A=[1,2,3;4,5,6;7,8,9]

A = 1     2     3

　　4     5     6

　　7     8     9

（2）利用已建好的矩阵建立更大的矩阵:一个大矩阵可以由已经建立好的小矩阵拼接而成。

>> A=[1,2,3;4,5,6;7,8,9];

>> B=[-1,-2,-3;-4,-5,-6;-7,-8,-9];

>> C=[A,B;B,A]

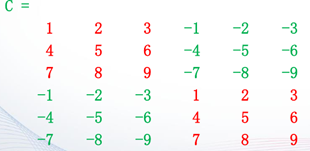
还可以用实部矩阵和虚部矩阵构成复数矩阵

>>B=[1,2,3;4,5,6];

>>C=[6,7,8;9,10,11];

>>A=B+i*C

A为同型矩阵，B为实部，C为虚部。i*C表示数与矩阵相乘。

2.冒号表达式

向量是矩阵的特殊类型，用：产生行向量。

如果省略步长e2，则步长为1。例如，t=0:5与t=0:1:5等价。

>> t=0:1:5

t = 0     1     2     3     4     5

还可以用linspace产生行向量。

当n省略时，自动产生100个元素。

>> x=linspace(0,pi,6)

x = 0    0.6283    1.2566    1.8850    2.5133    3.1416

3．结构矩阵和单元矩阵

（1）结构矩阵——把一组数据类型不同而逻辑上相关的数据组成一个有机的整体。

由结构数据构成的矩阵就是结构矩阵，结构矩阵里的每个元素就是结构数据类型。

格式为：

结构矩阵元素.成员名=表达式

就是给结构矩阵中的每个元素的每个成员分别赋值。

>> a(1).x1=10; a(1).x2='liu'; a(1).x3=[11,21;34,78];

>> a(2).x1=12; a(2).x2='wang'; a(2).x3=[34,191;27,578];

>> a(3).x1=14; a(3).x2='cai'; a(3).x3=[13,890;67,231];

（2）单元矩阵——每个元素可以由不同的数据类型组成的

建立单元矩阵和一般矩阵相似，直接输入就可以了，只是单元矩阵元素用大括号括起来

>> b= {10,'liu',[11,21;34,78];12,'wang',[34,191;27,578];... 14,'cai',[13,890;67,231]}

b =

[10]    'liu'      [2x2 double]

[12]    'wang'   [2x2 double]

[14]    'cai'     [2x2 double]

1.5矩阵元素的引用

l  矩阵元素的引用方式

l  利用冒号表达式获得子矩阵

l  利用空矩阵删除矩阵的元素

l  改变矩阵的形状

1．矩阵元素的引用方式   //下标为必须为正整数，且用圆括号括起来

（1）通过下标来引用矩阵的元素

A(3,2)表示A矩阵第3行第2列的元素。

>> A(3,2)=200

例：

>> A=[1,2,3;4,5,6];

>> A(4,5)=10

A = 1     2     3     0     0

　　4     5     6     0     0

　　0     0     0     0     0

　　0     0     0     0    10

注意：如果给出的行下标或列下标大于原来矩阵的行数和列数， 那么MATLAB将自动扩展原来的矩阵，并将扩展后没有赋值的矩阵元素置为0。

（2）通过序号来引用

l  在MATLAB中，矩阵元素按列存储，即首先存储矩阵的第一列元素，然后存储第二列元素，…，一直到矩阵的最后一列元素。

l  矩阵元素的序号就是矩阵元素在内存中的排列顺序。

例“”

>> A=[1,2,3;4,5,6]

A = 1     2     3

　　4     5     6

>> A(3)

ans = 2   //a12是第三号元素

序号与下标是一一对应的，以m×n矩阵A为例，矩阵元素A(i,j)的序 号为(j-1)×m+i

矩阵元素的序号与下标可以利用sub2ind和ind2sub函数实现转换。

sub2ind函数：将矩阵中指定元素的行、列下标转换成存储的序号。调用格

式为：

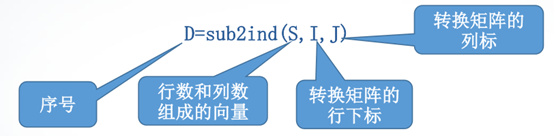
sub2ind函数举例。

>> A=[1:3;4:6]

A = 1     2     3

　　 4     5     6

>> D=sub2ind(size(A),[1,2;2,2],[1,1;3,2])   //i，j为矩阵，多个元素的行列下标转化为存储序号D与ij相同

D = 1     2

　　 6     4

ind2sub函数：将把矩阵元素的序号转换成对应的下标，其调用格式为：

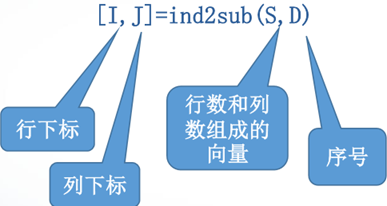
ind2sub函数举例。

>> [I,J]=ind2sub([3,3],[1,3,5])

I = 1     3     2

J = 1     1     2

2．利用冒号表达式获得子矩阵

子矩阵是指由矩阵中的一部分元素构成的矩阵。用单个：作为行/列下标，代表全部行/列。

A(i,:) 第i行的全部元素

A(:,j) 第j列的全部元素

A(i:i+m,k:k+m)   第i～i+m行内且在第k～k+m列中的所有元素

A(i:i+m,:) 第i～i+m行的全部元素

例子：

>> A=[1,2,3,4,5;6,7,8,9,10;11,12,13,14,15]

A = 1     2     3     4     5

　　6     7     8     9   10

　11   12     13   14   15

>> A(1:2,:)

ans = 1     2     3     4     5

　　6     7     8     9   10

>> A(2:3,1:2:5)

ans = 6     8   10

　　11   13   15

end运算符：表示某一维的末尾元素下标。

>>A=[1,2,3,4,5;6,7,8,9,10;11,12,13,14,15;16,17,18,19,20];

>>A(end,:)   //引用最后一行元素

ans = 16    17    18    19    20

>> A([1,4],3:end)   //引用第一行和第四行的从第三列到最后一列的元素

ans = 3     4     5

　　18    19    20

3．利用空矩阵删除矩阵的元素

空矩阵是指没有任何元素的矩阵。

>> x=[]

x = []

X是一个空矩阵。

>> A=[1,2,3,0,0;7,0,9,2,6;1,4,-1,1,8]

A = 1     2     3     0     0

　　7     0     9     2     6

　　1     4    -1     1     8

>> A(:,[2,4])=[]      //删除某些元素置位空矩阵就好了2和4列

A = 1     3     0

　　7     9     6

　　 1    -1     8

4．改变矩阵的形状

reshape(A,m,n)：在矩阵总元素保持不变的前提下，将矩阵A重新排成m×n的二维矩阵。

注意：reshape函数只是改变原矩阵的行数和列数，但并不改 变原矩阵元素个数及其存储顺序。

 

>> x=[23,45,65,34,65,34,98,45,78,65,43,76];

>> y=reshape(x,3,4)

Y= 23    34    98    65

　　45    65    45    43

　　 65    34    78    76

A(:) ：将矩阵A的每一列元素堆叠起来，成为一个列向量。

>> A =[-45,65,71;27,35,91]

A = -45    65    71

　　27    35    91

>> B=A(:)

B =

-45

27

65

35

71

91

即：A(:)等价于reshape(A,6,1)。