题目分享N
题意:有辆车,有r行,s*2列,在第s列和第s+1列之间有个过道,出口在第r+1行的过道处,现在给出每个人的位置(行号和列号),每人每次只能动一格,问最少耗费多长时间全员才能逃出去
分析:假如车上只有一个人,这个人位于x行y列,那他的逃生时间很好求
若y<=s,那所需时间就是s+1-y(走到过道)+r+1-x(在过道中走到出口)=s+r-x-y+2
若y>s,那其实可以将y对称到y'上,然后y'就能和y<=s时一样计算了,而y'=2*s+1-y,也就是说所需的时间是s+r-x-y'+2,其中y'=2*s+1-y
再进一步分析,假如车上有两个人,那么这两个人所需的时间怎么求呢?
很明显,如果这两个人不会相遇的话,所需的时间就是他们时间的最大值,而如果他们相遇的话,那么所需时间就要加一
那如何判断两人是否相遇呢?
假如两人位置分别为x1,y1 x2,y2 默认这两个人无论坐在过道的左侧还是右侧都对称到左侧考虑,为了方便计算,不需要分类讨论
那么这里就有一个问题到底能不能这么对称到左侧考虑呢?或者说如果有个人原来坐在右侧,如果让他做到左侧对称位置上去的话,会不会改变结果呢?
如果两个人恰好就是坐在对称的位置上,那么如果右侧不对称到左边的话,他们两人显然会在过道中间相遇
而对称到左边的话,右边的人显然和左边的人在没开始走的时候就发生了“相遇”,这里就必须要让一个人先走,此时另一个不动,然后他们再继续走,并且显然不会再相遇
但这貌似改变了两个人相遇的地点,不会改变结果吗?再回看到右边不对称到左边的时候,如果这两人在这时候也遵循一个先走,另一个不动的原则,然后他们再走就也不会相遇
也就是说对称与不对称可以用同一种走法来保证时间最大,也就是说走法相同且不影响结果
而如果两个人没有做到对称位置,那显然两个人在自己这行走到过道之前是不会与另一个人相遇的,而如果两个人在走到过道的时候相遇了,而右侧对称过去并走向过道所花的时间是相同的,自然也不会影 响相遇的结果,当然如果两人不相遇也是同理的
所以将右侧对称到左边的考虑是对结果以及运动过程没有影响的,那么这两个人到达对应行过道的时间就是s+1-y1和s+1-y2,而如果x1<=x2,那么他们到达x2行的过道所花的时间就是s+1-y1+x2-x1和s+1-y2,而且他们俩相遇也只可能在这里相遇,并且相遇的条件是到达该地的时间相等,即s+1-y1+x2-x1=s+1-y2,将x2移到右边,并给等式两边都加(r+1)就可以得到s+r-x1-y1+2=s+r-x2-y2+2,这正好是两人单独走到出口所用的时间,也就是说两人相遇与他们到达出口时间相等是等价的
而如果两个人在路上发生了相遇,那么就需要让一个人先走,而和他相遇的其他人要留在原地,当然在这时候可能会有其他人走到这个相遇的位置,那么这段过程的实质就是相遇地点中的一个人与没有相遇的人,到达出口所需的时间-1,其他人不变,那么如何用程序来模拟这个过程呢?
其实很简单,因为每次只能有一个人从出口出去,而且出去的顺序一定是耗时少的在前,耗时多的在后,所以将所有人所需时间排好序之后,用一个变量记录当前的人出去所用的时间,如果遇到相等的话就+1,如果所需时间小于当前时间的话那就说明这个人后来也被堵在了相遇的地方,那也+1,如果没有发生相遇也就是所需时间大于当前的时间,那么就可以将当前时间附成该人所需时间即可
代码: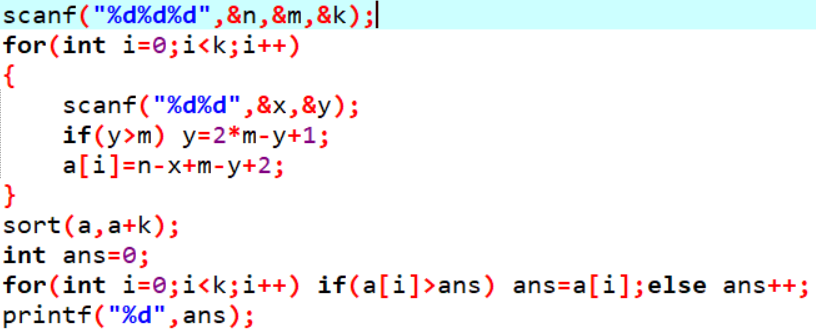
题目分享N的更多相关文章
- 2019年腾讯PHP程序员面试题目分享
有需要学习交流的友人请加入交流群的咱们一起,有问题一起交流,一起进步!前提是你是学技术的.感谢阅读! 点此加入该群jq.qq.com 1. php 的垃圾回收机制 PHP 可以自动进行内存管理,清除 ...
- 20190924-LeetCode解数独题目分享
解决数独 题目描述 编写一个程序,通过已填充的空格来解决数独问题. 一个数独的解法需遵循如下规则: 数字 1-9 在每一行只能出现一次. 数字 1-9 在每一列只能出现一次. 数字 1-9 在每一个以 ...
- 题目分享E 二代目
题意:一棵点数为n的树,每个节点有点权,要求在树中中找到一个最小的x,使得存在一个点满足max(该点点权,该点相邻的点的点权+1,其他点的点权+2)=x 分析:首先要能把题目转化为上述题意 首先题目让 ...
- 题目分享D 二代目
题意:给定一个T条边的无向图,求S到E恰好经过N条边的最短路径 T≤100 N≤1000000 分析:(据说好像假期学长讲过) 首先很容易想到的是dp[i][j][k]表示从i到j经过k条边的最短路径 ...
- 题目分享C 二代目
题意:一个数列是由 1 1 2 1 2 3 1 2 3 4 1 2 3 4 5 1 2 3 4 5 6.....组成,也就是1-1,1-2,1-3......并且如果遇到多位数也要拆成数字比如1-10 ...
- 题目分享X
题意:一张票有n位数,如果这张票的前一半数字的和等于后一半数字的和(n一定是偶数),就称这张票为快乐票.有些数被擦除了,标记为’?’(’?‘的个数也是偶数),现在Monocarp 和 Bicarp 进 ...
- 题目分享V
题意:现在两个人做游戏,每个人刚开始都是数字1,谁赢了就能乘以k^2,输的乘以k(k可以是任意整数,每次不一定相同)现在给你最终这两个人的得分,让你判断是否有这个可能,有可能的话Yes,否则No. 分 ...
- 题目分享T
题意:蛐蛐国里现在共有n只蚯蚓(n为正整数).每只蚯蚓拥有长度,我们设第i只蚯蚓的长度为a_i(i=1,2,...,n),并保证所有的长度都是非负整数(即:可 能存在长度为0的蚯蚓).每一秒,神刀手会 ...
- 题目分享P
题意: 给出一棵n个节点的树,这棵树的每条边有一个权值,这个权值只可能是0或1. 在一局游戏开始时,会确定一个节点作为根.接下来从女生开始,双方轮流进行 操作.当一方操作时,他们需要先选择一个不为根的 ...
- 题目分享H 二代目
题意:有m个限制,每个限制l1,r1,l2,r2四个数,限制了一个长度为n的数第l1到r1位要与第l2到r2相同,保证r1-l1=r2-l2,求在限制下一共有多少种数 分析: 暴力的话肯定是从l1-r ...
随机推荐
- String、StringBuffer、StringBuilder葫芦三兄弟
今年因为疫情的原因,本打算在读研期间好好做项目,写论文,在今年9月份能找个好工作,但现在迟迟不能开学,也无法正常的给导师打工,所以干脆就打算好好准备工(fan)作(wan)的事儿. 接触Java也有好 ...
- 选择排序(C++,Java,Python实现)
排序算法之选择排序,选择排序,选择排序的基本思想描述为:每一趟在n-i+1(i=1,2,-,n-1)个记录中选取关键字最小的记录作为有序序列中第i个记录.具体来说,假设长度为n的数组arr,要按照从小 ...
- bootstrapTest
<!DOCTYPE html><html lang="zh-CN"> <head> <meta charset="utf-8&q ...
- 【java 数据结构】还不会二叉树?一篇搞定二叉树
二叉树是我们常见的数据结构之一,在学习二叉树之前我们需要知道什么是树,什么是二叉树,本篇主要讲述了二叉树,以及二叉树的遍历. 你能get到的知识点? 1.树的介绍 2.二叉树的介绍 3.二叉树遍历的四 ...
- 搭建WEB、NFS共享、sersync实时同步以及全网定时备份服务流程
本次实验的主要目的: 1.搭建web服务,使用nfs服务共享的/data目录挂载到web站点目录上. 2.nfs服务器与backup服务器使用sersync实时同步/data目录中的文件. 3.bac ...
- 【FreeMarker】【程序开发】数据模型,对象包装
[FreeMarker][程序开发]数据模型,对象包装 分类: Java.FreeMarker2014-10-25 18:49 413人阅读 评论(0) 收藏 举报 FreeMarker 目录(? ...
- ftl中几个特殊的用法
@ 注意${}为变量的渲染显示,即先计算后打印出来,而<>里面为定义等操作符的定义 ,而首尾2个<>中间部分一般为计算打印部分 @数据模型中如果不是以map数据来封装的,而是直 ...
- Volatile可见性分析(一)
JUC(java.util.concurrent) 进程和线程 进程:后台运行的程序(我们打开的一个软件,就是进程) 线程:轻量级的进程,并且一个进程包含多个线程(同在一个软件内,同时运行窗口,就是线 ...
- 运输层--------运输层与网络层的关系、UDP、TCP
一.运输层与网络的区别: 网络层提供了主机之间的逻辑通信,而运输层为运行在不同主机上的进程之间提供了逻辑通信 二.实例证明: 考虑有两个家庭,一家位于美国东岸,一家位于美国西海岸,每家有12孩子.东海 ...
- 深度解密 Go 语言之 sync.Pool
最近在工作中碰到了 GC 的问题:项目中大量重复地创建许多对象,造成 GC 的工作量巨大,CPU 频繁掉底.准备使用 sync.Pool 来缓存对象,减轻 GC 的消耗.为了用起来更顺畅,我特地研究了 ...
