MATLAB神经网络（7） RBF网络的回归——非线性函数回归的实现

7.1 案例背景

7.1.1 RBF神经网络概述

径向基函数是多维空间插值的传统技术，RBF神经网络属于前向神经网络类型，网络的结构与多层前向网络类似，是一种三层的前向网络。第一层为输入层，由信号源结点组成；第二层为隐藏层，隐藏层节点数视所描述问题的需要而定，隐藏层中神经元的变换函数即径向基函数是对中心点径向对称且衰减的非负非线性函数，该函数是局部响应函数，而以前的前向网络变换函数都是全局响应的函数；第三层为输出层，它对输入模式作出响应。
RBF网络的基本思想是：用RBF作为隐单元的“基”构成隐藏层空间，隐含层对输入矢量进行变换，将低维的模式输入数据变换到高维空间内，使得在低维空间内的线性不可分的问题在高维空间内线性可分。
RBF神经网络结构简单、训练简洁而且学习收敛速度快，能够逼近任意非线性函数，因此已被广泛应用于时间序列分析、模式识别、非线性控制和图形处理等领域。

7.1.2 RBF神经网络结构模型

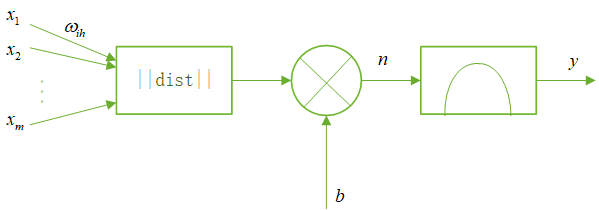
径向基神经网络的节点激活函数采用径向基函数，通常定义为空间任一点到某一中心之间的欧式距离的单调函数。

径向基神经网络的激活函数是以输入向量和权值向盘之间的距离$\left| {\left| {dist} \right|} \right|$作为自变量的。径向基神经网络的激活函数的一般表达式为\[R\left( {\left| {\left| {dist} \right|} \right|} \right) = {e^{ - {{\left| {\left| {dist} \right|} \right|}^2}}}\]随着权值和输入向量之间距离的减少，网络输出是递增的，当输入向量和权值向量一致时，神经元输出为1。图中的$b$为阔值，用于调整神经元的灵敏度。利用径向基神经元和线性神经元可以建立广义回归神经网络，此种神经网络适用于函数逼近方面的应用；径向基神经元和竞争神经元可以建立概率神经网络，此种神经网络适用于解决分类问题。

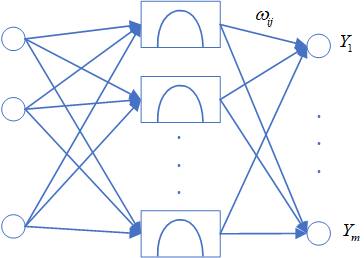
RBF神经网络中，输入层仅仅起到传输信号的作用，与前面所讲述的神经网络相比较，输入层和隐含层之间可以看作连接权值为1的连接，输出层和隐含层所完成的任务是不同的，因而它们的学习策略也不相同。输出层是对线性权进行调整，采用的是线性优化策略，因而学习速度较快。而隐含层是对激活函数（格林函数或高斯函数，一般取高斯函数）的参数进行调整，采用的是非线性优化策略，因而学习速度较慢。

7.1.3 RBF神经网络的学习算法

RBF神经网络学习算法需要求解的参数有3个：基函数的中心、方差以及隐含层到输出层的权值。根据径向基函数中心选取方法的不同，RBF网络有多种学习方法，如随机选取中心法、自组织选取法、有监督选取中心法和正交最小二乘法等。下面将介绍自组织选取中心的RBF神经网络学习法。该方法由两个阶段组成：一是自组织学习阶段，此阶段为无导师学习过程，求解隐含层基函数的中心与方差；二是有导师学习阶段，此阶段求解隐含层到输出层之间的权值。

径向基神经网络中常用的径向基函数是高斯函数，因此径向基神经网络的激活函数可表示为\[R({x_p} - {c_i}) = \exp \left( { - \frac{1}{{2{\sigma ^2}}}{{\left| {\left| {{x_p} - {c_i}} \right|} \right|}^2}} \right)\]式中${\left| {\left| {{x_p} - {c_i}} \right|} \right|}$为欧式范数，$c_{i}$为高斯函数的中心，$\sigma$为高斯函数的方差。

径向基网络的输出为\[{y_j} = \sum\limits_{i = 1}^h {{\omega _{ij}}R({x_p} - {c_i})} \;\;\;j = 1,2, \ldots ,n\]式中${x_p} = {({x_1}^p,{x_2}^p, \ldots ,{x_m}^p)^T}$为第$p$个输入样本，$p = 1,2, \ldots ,P$，$P$为样本总数，$c_{i}$为网络隐含层结点的中心，${{\omega _{ij}}}$为隐含层到输出层的链接权值，$i = 1,2, \ldots ,h$