Kmeans应用

1、思路

应用Kmeans聚类时，需要首先确定k值，如果k是未知的，需要先确定簇的数量。其方法可以使用拐点法、轮廓系数法（k>=2）、间隔统计量法。若k是已知的，可以直接调用sklearn子模块cluster中Kmeans方法，对数据进行切割。

另外如若数据集不规则，存在量纲上的差异，也需要对其进行标准化处理。

2、数据的标准化处理

（minmax_scale为sklearn子模块processing 中 的函数），第一种方法为压缩变量为mean=0,std=1的无量纲数据，第二种方式会压缩变量为[0,1]之间无量纲数据　。

3、案例

1）对iris聚类（已知簇类的情况）

情况1，已知k值，k=3

调用KMeans模块

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from  sklearn.cluster  import KMeans
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']

iris = pd.read_csv(r'iris.csv')

# 设置聚为3类，n_clusters =3
X = iris.drop(labels = 'Species',axis = 1)
kmeans = KMeans(n_clusters =3 )
kmeans.fit(X)

X['cluster'] = kmeans.labels_
X.cluster.value_counts()

# 绘制花瓣长度与宽度的散点图
import seaborn as sns

centers = kmeans.cluster_centers_
print(centers)
sns.lmplot(x = 'Petal_Length',
           y=  'Petal_Width',
           hue = 'cluster',
           markers = ['^','s','o'],
           data = X,
           fit_reg= False,
           scatter_kws = {'alpha':0.8},
           legend_out = False
          )
plt.scatter(centers[:,2], centers[:,3], marker = '*',color = 'black', s =130)  # 绘制簇中心点
plt.xlabel('花瓣长度')
plt.ylabel('花瓣宽度')
plt.show()

iris['Species_map'] = iris.Species.map({'virginica':0,'setosa':1,"versicolor":2})  # 3种类型进行映射到0，1,2
sns.lmplot(x = 'Petal_Length',
           y=  'Petal_Width',
           hue = 'Species_map',
           markers = ['^','s','o'],
           data = iris,
           fit_reg= False,
           scatter_kws = {'alpha':0.8},
           legend_out = False  )
plt.xlabel('花瓣长度')
plt.ylabel('花瓣宽度')
plt.show()

生成图形如下：

 

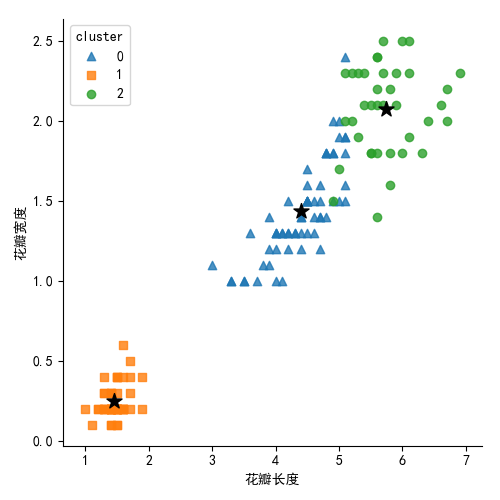
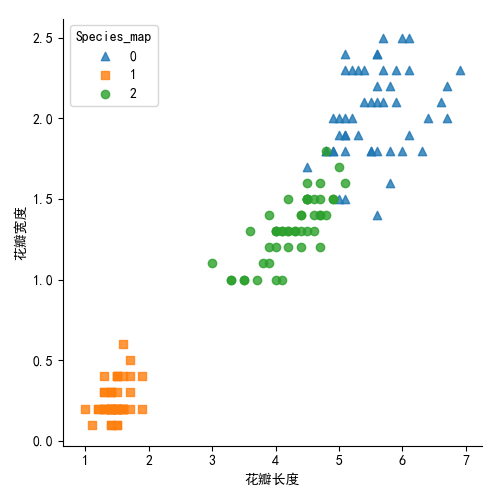
对簇中心做雷达图

import pygal

radar_chart = pygal.Radar(fill = True)
radar_chart.x_labels = ['花萼长度','花萼宽度', '花瓣长度','花瓣宽度']

# 雷达图区域绘制
radar_chart.add('C1',centers[0])
radar_chart.add('C2',centers[1])
radar_chart.add('C3',centers[2])
radar_chart.render_to_file('radar_chart.svg')

　　生成如下图形，C1类型的花，花萼长和花瓣长都是最大的。C2类型的花，对应的3个指标值都比较小，C3类型的花，3个指标的平均值，恰好落在C1和C2之间。

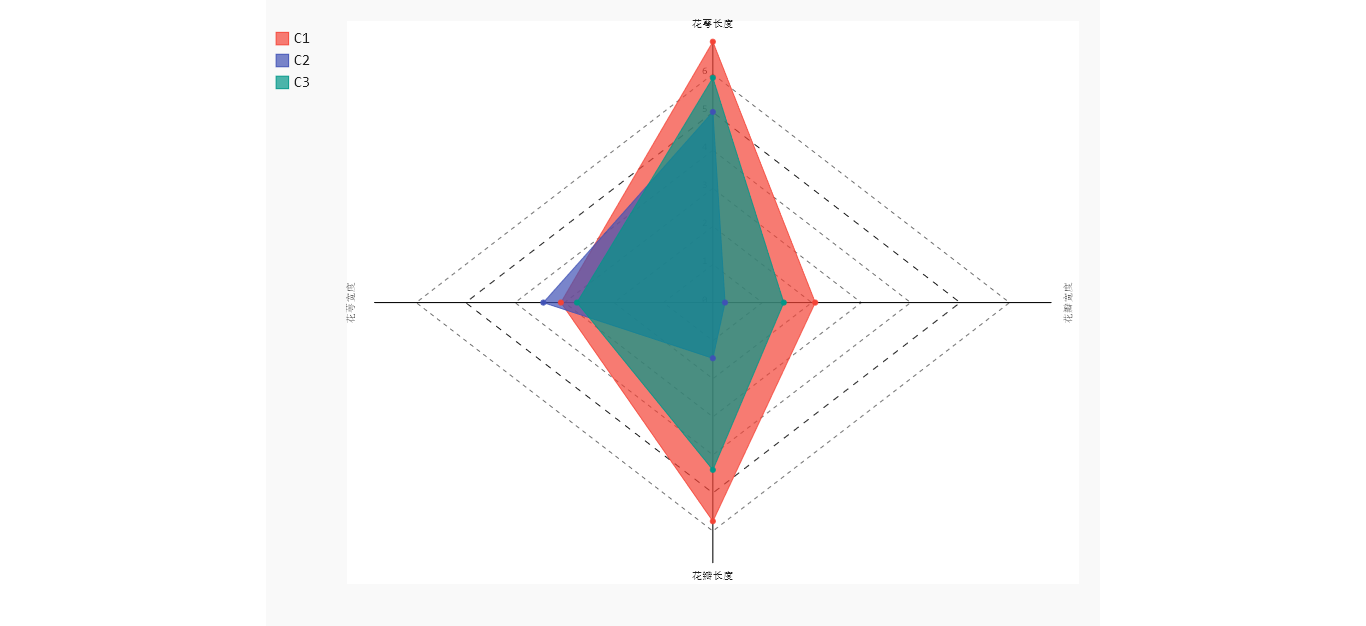
2）NBA球员数据集聚类（未知k值）

数据集

选定得分、命中率，三分命中率，罚球命中率四个维度进行分析，观察数据情况，需进行标准化。

• 先对得分和命中率作散点图，进行观察

sns.lmplot(x = '得分',
           y = '命中率',
          data = players,
           fit_reg = False,
           scatter_kws = {'alpha': 0.8,'color': 'steelblue'}
          )

plt.show()

　　

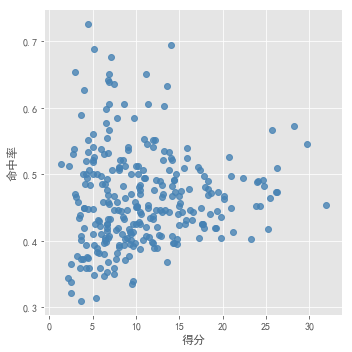
肉眼无法进行观察数据集适合分为几个簇。分别采用 以上确定k值的3种方法进行测试。

拐点法：

from sklearn import preprocessing

X = preprocessing.minmax_scale(players[['得分','罚球命中率','命中率','三分命中率']])   # 数据集的标准化
X = pd.DataFrame(X, columns=['得分','罚球命中率','命中率','三分命中率'])
k_SSE(X,15)

　　

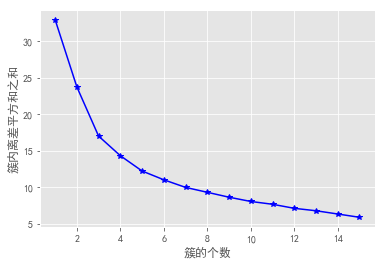
结果看出，k值在3、4斜率变化比较明显，在5以后斜率保持一定的水平。所以k取3,4,5均有可能。在比较其他方法。

轮廓系数法及Gap statistic法可视化效果如下：

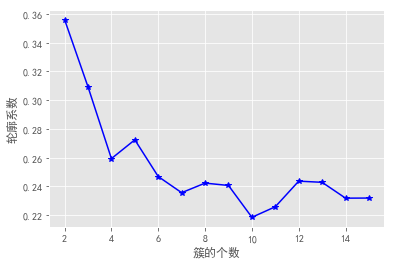
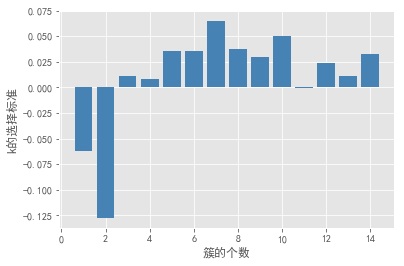
结合上图，轮廓系数在大于0的情况下，最大值对应的k值为2，统计量法首次出现正值的k值为3，综合考虑以上三种方法取k值为3，即将数据集分为3个簇最理想。

• 对得分和命中率进行聚类

kmeans = KMeans(n_clusters = 3)
kmeans.fit(X)
players['cluster'] = kmeans.labels_
centers = []

for i in players.cluster.unique():
    centers.append(players.ix[players.cluster == i, ['得分','罚球命中率','命中率','三分命中率']].mean())

centers = np.array(centers)

sns.lmplot(x = '得分',
           y = '命中率',
           hue = 'cluster',
           data = players,
           markers = ['^','s','o'],
           fit_reg = False,
           scatter_kws = {'alpha': 0.8},
           legend = False
)
plt.scatter(centers[:,0],centers[:,2],c = 'k',marker = '*',s =180)
plt.xlabel('得分')
plt.ylabel('命中率')
plt.show()

# 雷达图绘制
centers_std = kmeans.cluster_centers_
radar_chart = pygal.Radar(fill = True) # 设置填充型雷达图
radar_chart.x_labels = ['得分','罚球命中率','命中率','三分命中率']
radar_chart.add('C1', centers_std[0])
radar_chart.add('C2', centers_std[1])
radar_chart.add('C3', centers_std[2])

radar_chart.render_to_file('radar_charts.svg')

　结果如下图：

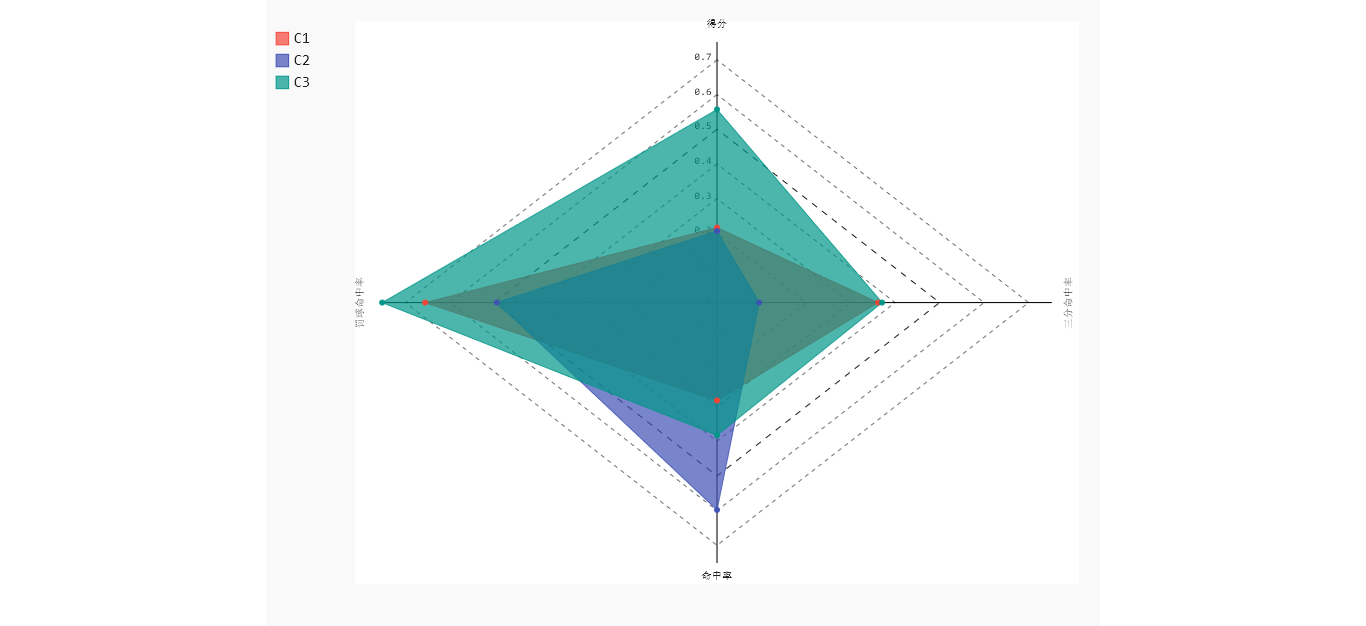
由聚类结果可以发现，三角形区域代表的球员属于低得分低命中率类型，命中率普遍低于50%，方形区域代表低得分高命中率的球员，圆形区域球员与三角形区域球员具有类似的命中率，单圆形区域球员具有高得分。且该区域存在部分球员具有高得分且高命中率。通过对比雷达图，C1、C2类球员平均得分差不多，但C2具有更高的命中率。平均罚球命中率和三分球命中率上来看，C1球员也要明显高于C2.